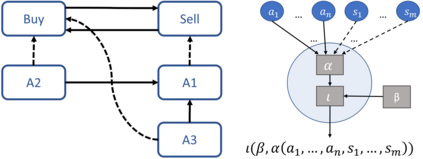
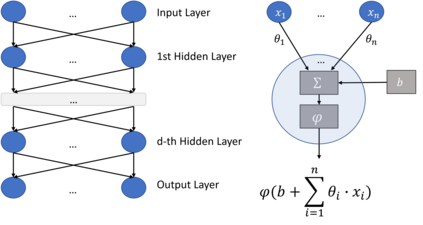
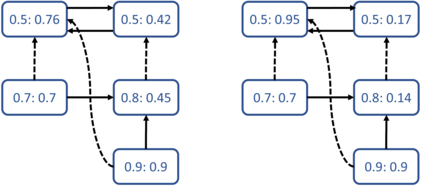
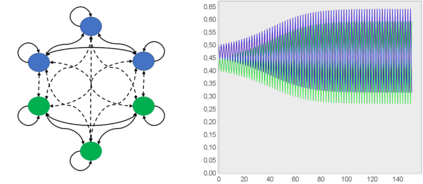
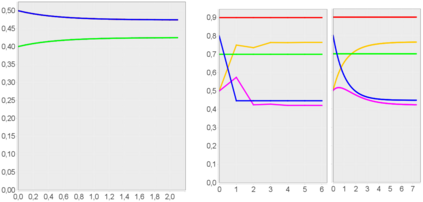
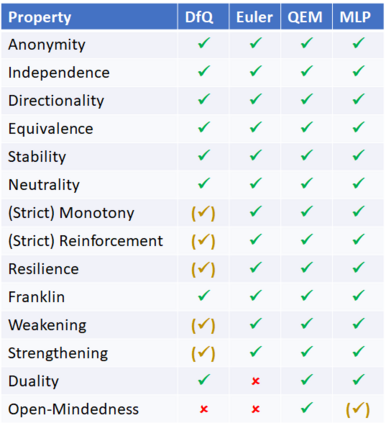
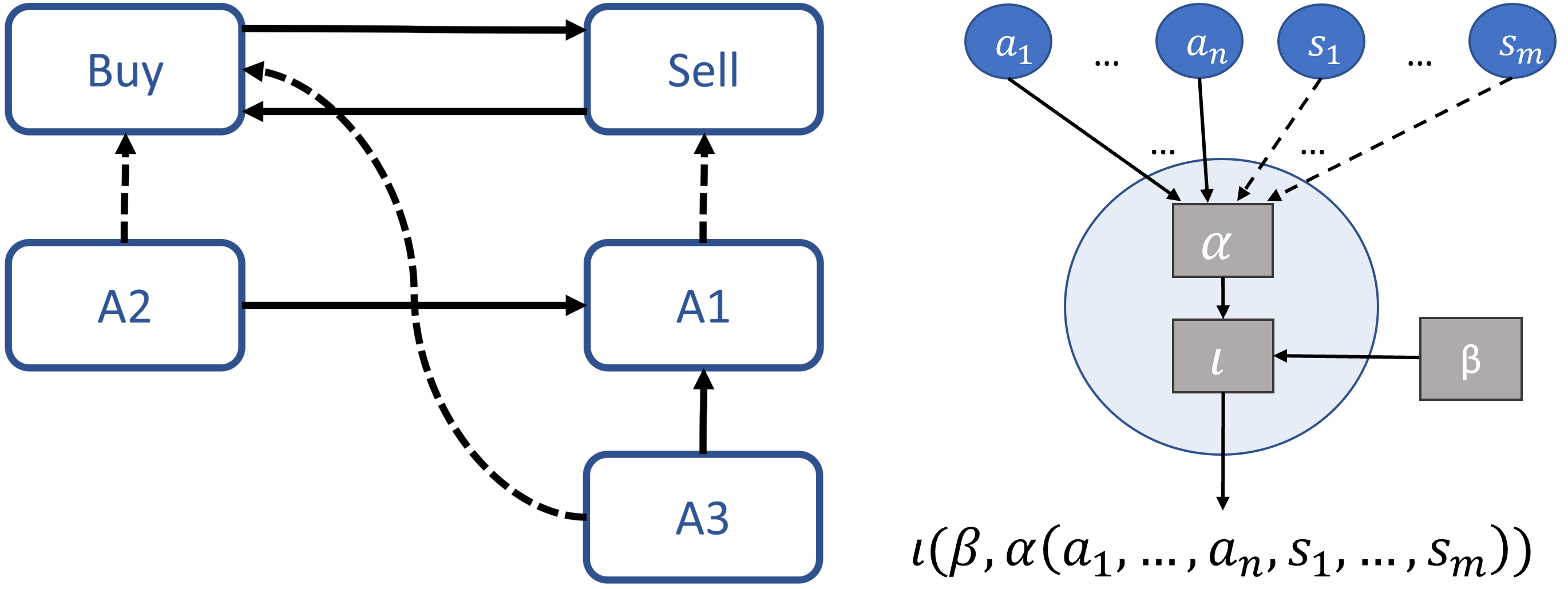
We show that an interesting class of feed-forward neural networks can be understood as quantitative argumentation frameworks. This connection creates a bridge between research in Formal Argumentation and Machine Learning. We generalize the semantics of feed-forward neural networks to acyclic graphs and study the resulting computational and semantical properties in argumentation graphs. As it turns out, the semantics gives stronger guarantees than existing semantics that have been tailor-made for the argumentation setting. From a machine-learning perspective, the connection does not seem immediately helpful. While it gives intuitive meaning to some feed-forward-neural networks, they remain difficult to understand due to their size and density. However, the connection seems helpful for combining background knowledge in form of sparse argumentation networks with dense neural networks that have been trained for complementary purposes and for learning the parameters of quantitative argumentation frameworks in an end-to-end fashion from data.
翻译:我们展示了一个有趣的向导神经网类可以被理解为定量参数框架。 这种连接在正式参数和机器学习的研究之间建立了桥梁。 我们把向导神经网的语义概括为循环图,并在参数图中研究由此产生的计算和语义特性。 事实证明,语义比为论证设置而专门设计的现有语义提供了更强有力的保障。 从机器学习的角度看,这种连接似乎没有立即起到帮助作用。 虽然它给某些向导神经网提供了直观的意义,但由于它们的规模和密度,它们仍然难以理解。 然而,这种连接似乎有助于将背景知识以稀疏的参数网络与密集神经网络相结合,而这些网络经过培训是为了互补目的,并且是为了从数据中以端到端的方式学习定量参数。