Deciding All Behavioral Equivalences at Once: A Game for Linear-time--Branching-time Spectroscopy

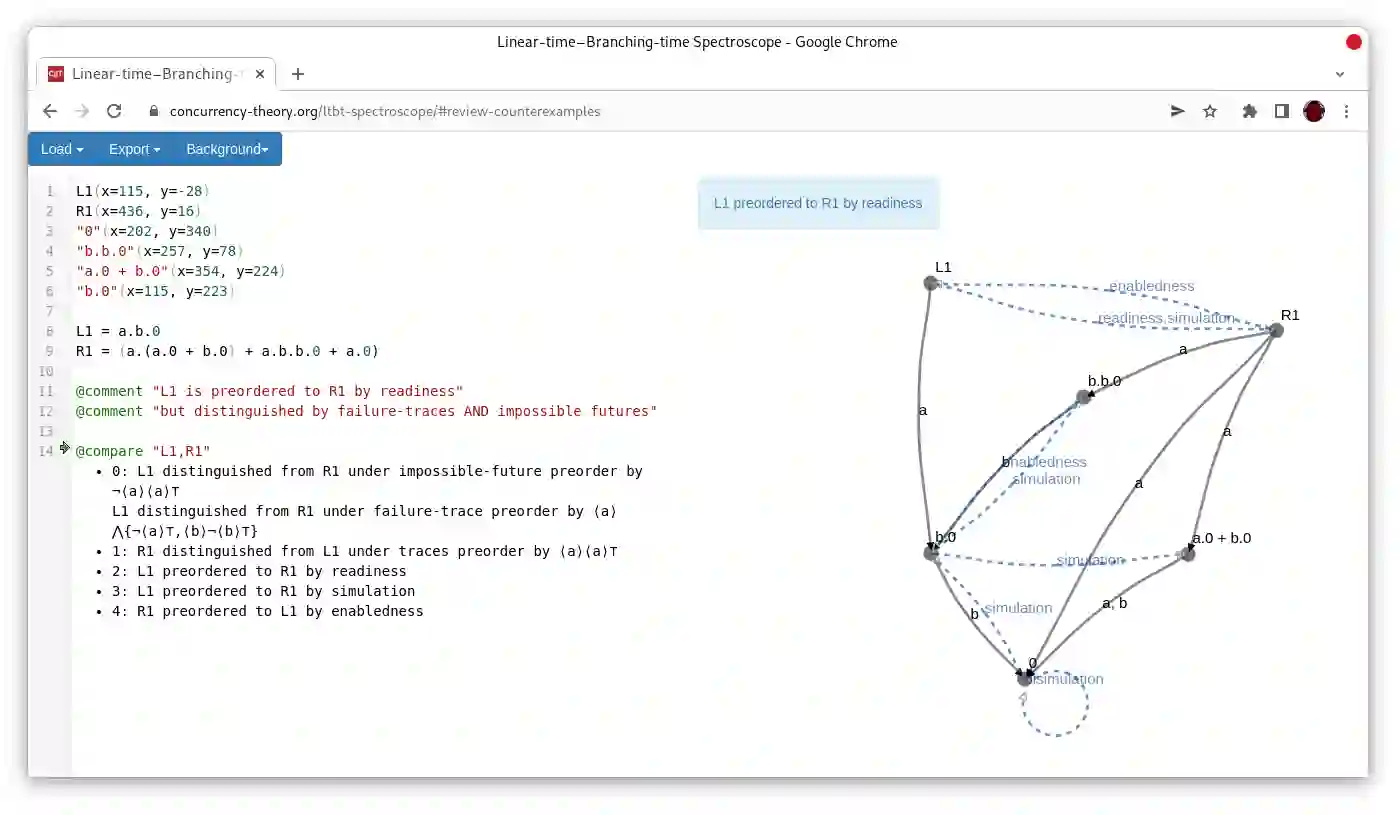
We introduce a generalization of the bisimulation game that finds distinguishing Hennessy--Milner logic formulas from every finitary, subformula-closed language in van Glabbeek's linear-time--branching-time spectrum between two finite-state processes. We identify the relevant dimensions that measure expressive power to yield formulas belonging to the coarsest distinguishing behavioral preorders and equivalences; the compared processes are equivalent in each coarser behavioral equivalence from the spectrum. We prove that the induced algorithm can determine the best fit of (in)equivalences for a pair of processes.