Byzantine Fault-Tolerance in Federated Local SGD under 2f-Redundancy

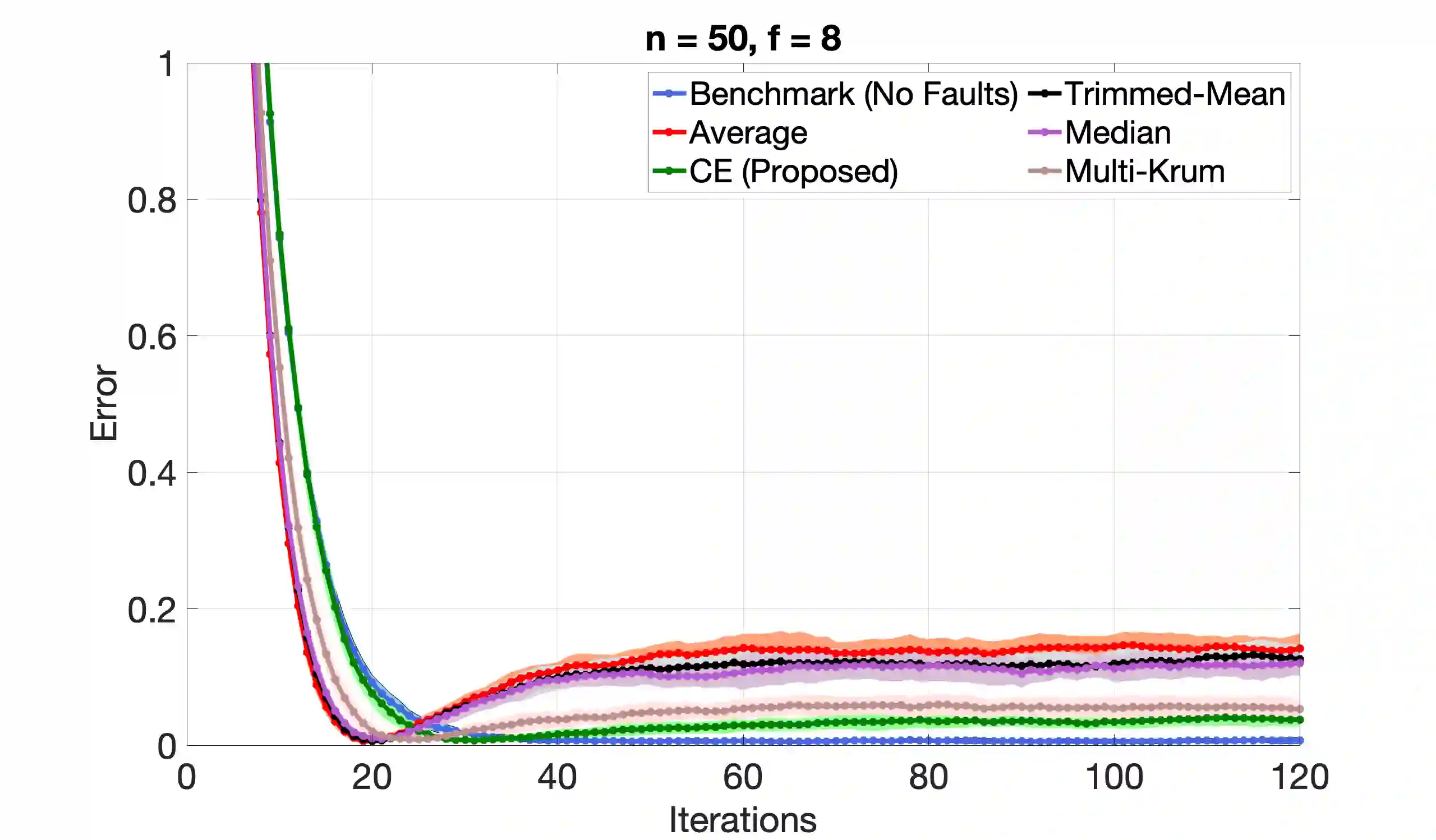
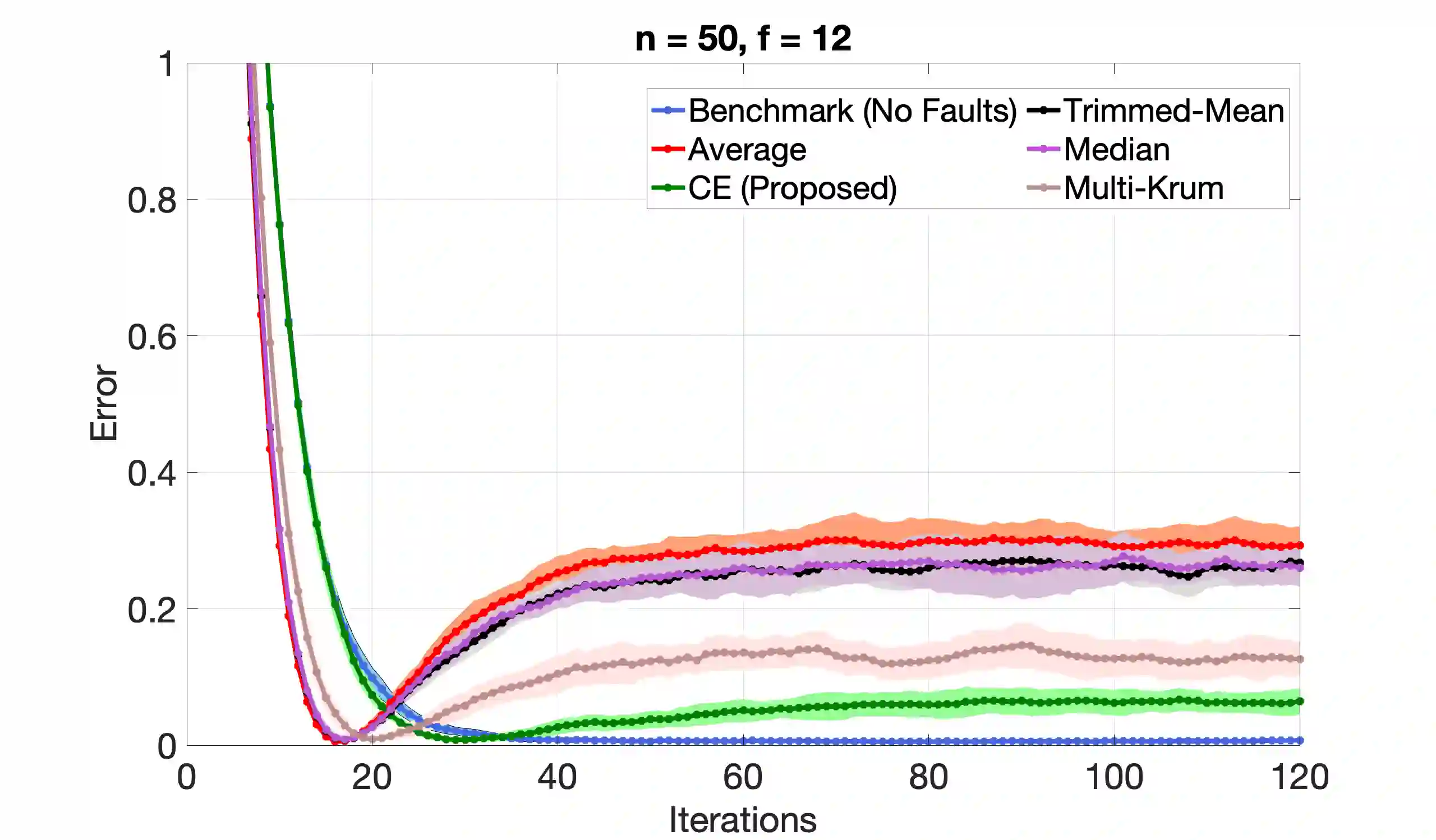
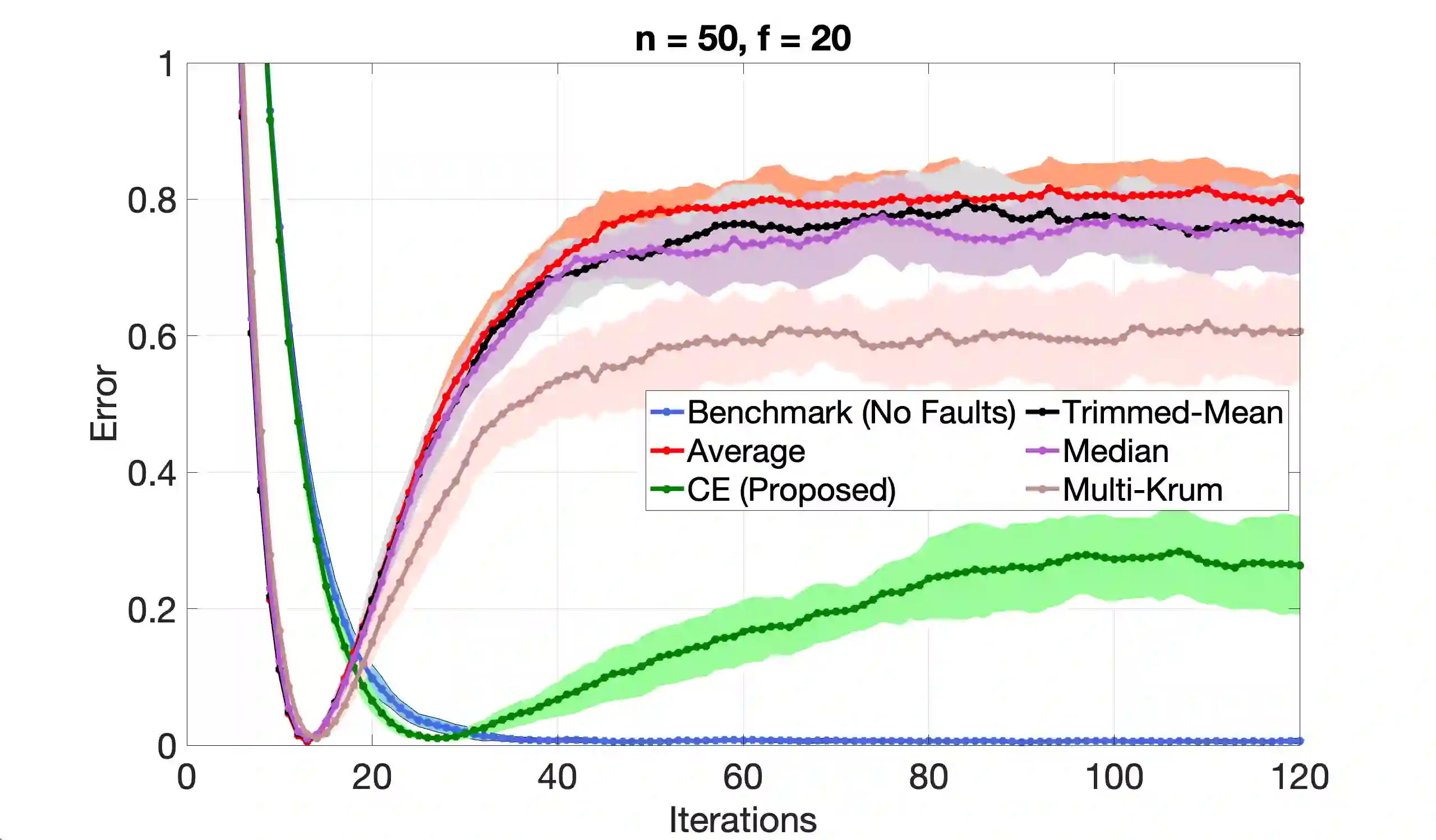
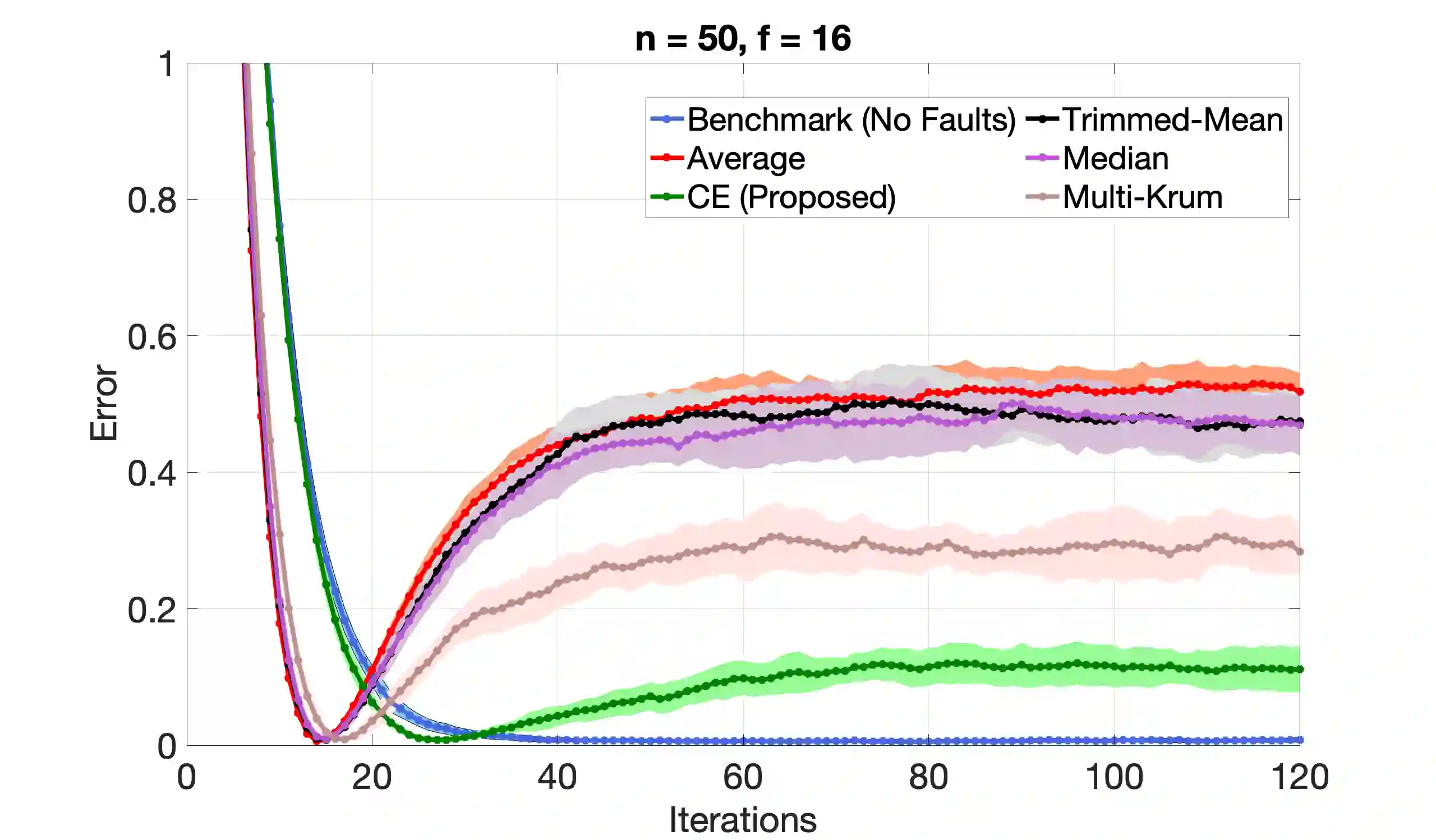
We consider the problem of Byzantine fault-tolerance in federated machine learning. In this problem, the system comprises multiple agents each with local data, and a trusted centralized coordinator. In fault-free setting, the agents collaborate with the coordinator to find a minimizer of the aggregate of their local cost functions defined over their local data. We consider a scenario where some agents ($f$ out of $N$) are Byzantine faulty. Such agents need not follow a prescribed algorithm correctly, and may communicate arbitrary incorrect information to the coordinator. In the presence of Byzantine agents, a more reasonable goal for the non-faulty agents is to find a minimizer of the aggregate cost function of only the non-faulty agents. This particular goal is commonly referred as exact fault-tolerance. Recent work has shown that exact fault-tolerance is achievable if only if the non-faulty agents satisfy the property of $2f$-redundancy. Now, under this property, techniques are known to impart exact fault-tolerance to the distributed implementation of the classical stochastic gradient-descent (SGD) algorithm. However, we do not know of any such techniques for the federated local SGD algorithm - a more commonly used method for federated machine learning. To address this issue, we propose a novel technique named comparative elimination (CE). We show that, under $2f$-redundancy, the federated local SGD algorithm with CE can indeed obtain exact fault-tolerance in the deterministic setting when the non-faulty agents can accurately compute gradients of their local cost functions. In the general stochastic case, when agents can only compute unbiased noisy estimates of their local gradients, our algorithm achieves approximate fault-tolerance with approximation error proportional to the variance of stochastic gradients and the fraction of Byzantine agents.