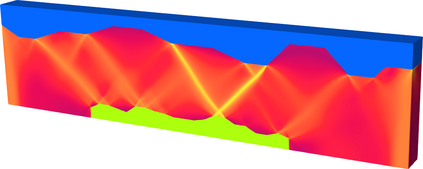
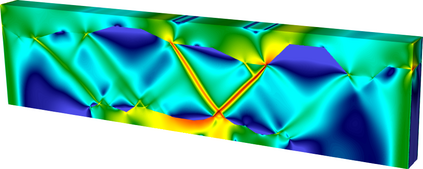
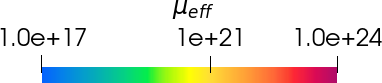
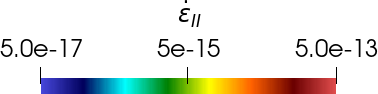We present augmented Lagrangian Schur complement preconditioners and robust multigrid methods for incompressible Stokes problems with extreme viscosity variations. Such Stokes systems arise, for instance, upon linearization of nonlinear viscous flow problems, and they can have severely inhomogeneous and anisotropic coefficients. Using an augmented Lagrangian formulation for the incompressibility constraint makes the Schur complement easier to approximate, but results in a nearly singular (1,1)-block in the Stokes system. We present eigenvalue estimates for the quality of the Schur complement approximation. To cope with the near-singularity of the (1,1)-block, we extend a multigrid scheme with a discretization-dependent smoother and transfer operators from triangular/tetrahedral to the quadrilateral/hexahedral finite element discretizations $[\mathbb{Q}_k]^d\times \mathbb{P}_{k-1}^{\text{disc}}$, $k\geq 2$, $d=2,3$. Using numerical examples with scalar and with anisotropic fourth-order tensor viscosity arising from linearization of a viscoplastic constitutive relation, we confirm the robustness of the multigrid scheme and the overall efficiency of the solver. We present scalability results using up to 28,672 parallel tasks for problems with up to 1.6 billion unknowns and a viscosity contrast up to ten orders of magnitude.
翻译:我们为不压缩的Stencial Stokes问题提供了强化的 Lagrangian Schur 补充性先决条件和强大的多格格方法, 并具有极端的粘度差异性。 例如, 在非线性粘度流动问题线性化时, 这些Stokes 系统就会产生这样的问题, 并且它们可能具有严重的不相容性和厌异性系数。 使用一个增强的Lagrangian 配方来抑制性限制, 使得Schur 的配方更容易补充到近似值, 但是在Stokes系统中导致一个几乎奇异数(1, 1)- 块。 我们为Schur 补充性近似的质量提出估计值。 为了应对( 1, 1) 区块的接近性问题, 我们扩展一个多格计划, 其离散性、 平滑度和转移操作者从三角/ 色度 和异性元素分解性分解性分解性分解性分解性, 使Schurrangical- coltical Protical Protical Protical Protical Protitution 。 使用一个不相 和不相正数级的不相联 。,,, 从一个不相正数级的不相形的不相形的不相形性图性图性图性图性 和正成的不相比性图性, 。