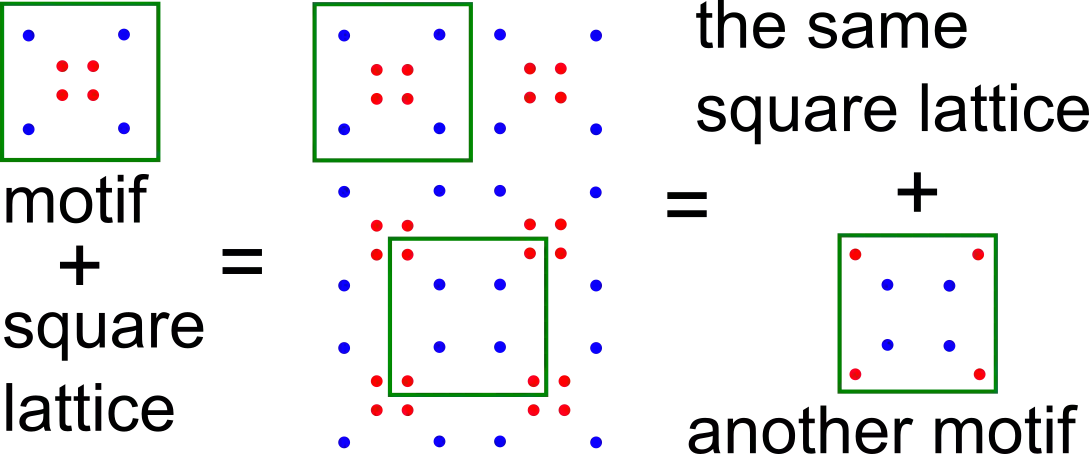
The fundamental model of all solid crystalline materials (periodic crystals) is a periodic set of atomic centers considered up to rigid motion in Euclidean space. The major obstacle to materials discovery was highly ambiguous representations that didn't allow fast and reliable comparisons, and led to numerous (near-) duplicates in all experimental databases. This paper introduces the new invariants that are crystal descriptors without false negatives and are called Pointwise Distance Distributions (PDD). The PDD invariants are numerical matrices with a near-linear time complexity and an exactly computable metric. The strongest theoretical result is generic completeness (absence of false positives) for all finite and periodic sets of points in any dimension. The strength of PDD is demonstrated by 200B+ pairwise comparisons of all 660K+ periodic structures from the world's largest Cambridge Structural Database of 1.17M+ known crystals over two days on a modest desktop.
翻译:所有固体晶体材料(定期晶体)的基本模型是一套周期性原子中心,在欧几里得空间被认为是僵硬的运动。材料发现的主要障碍是高度模糊的表述,无法进行快速和可靠的比较,导致所有实验数据库中出现大量(近)重复。本文件介绍了新的变量,这些新变量是晶体描述器,没有假底片,称为Pointwith距离分布(PDD) 。PDD变量是数字矩阵,具有近线性时间复杂性,精确的可比较度量度。最强的理论结果是任何层面所有定点和定期点的通用完整性(没有假阳性),PDDD的强度通过200B+双对全世界最大的剑桥结构数据库(1.17M+已知晶体)的660K+周期结构的强性对比来证明,该数据库为期两天,在一个小的桌面上是1.17M+已知晶体。