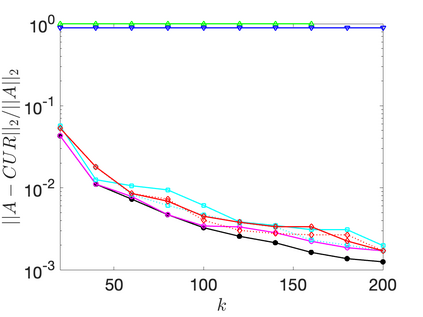
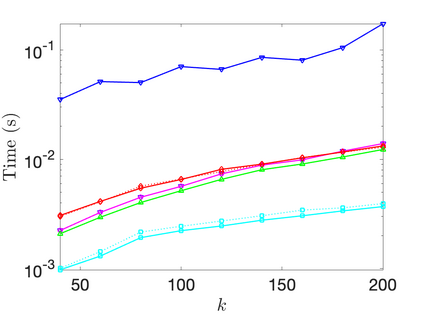
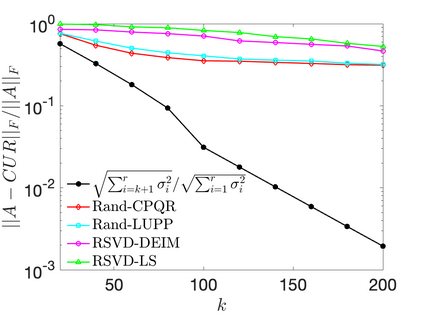
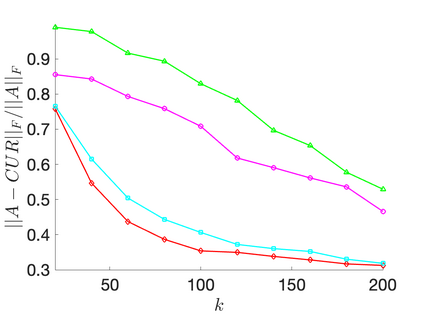
The CUR decomposition is a technique for low-rank approximation that selects small subsets of the columns and rows of a given matrix to use as bases for its column and rowspaces. It has recently attracted much interest, as it has several advantages over traditional low rank decompositions based on orthonormal bases. These include the preservation of properties such as sparsity or non-negativity, the ability to interpret data, and reduced storage requirements. The problem of finding the skeleton sets that minimize the norm of the residual error is known to be NP-hard, but classical pivoting schemes such as column pivoted QR work tend to work well in practice. When combined with randomized dimension reduction techniques, classical pivoting based methods become particularly effective, and have proven capable of very rapidly computing approximate CUR decompositions of large, potentially sparse, matrices. Another class of popular algorithms for computing CUR de-compositions are based on drawing the columns and rows randomly from the full index sets, using specialized probability distributions based on leverage scores. Such sampling based techniques are particularly appealing for very large scale problems, and are well supported by theoretical performance guarantees. This manuscript provides a comparative study of the various randomized algorithms for computing CUR decompositions that have recently been proposed. Additionally, it proposes some modifications and simplifications to the existing algorithms that leads to faster execution times.
翻译:CUR 分解是一种低级近似技术,它选择某一矩阵的列和行的小子集,作为其列和行的基数。它最近吸引了很大的兴趣,因为它比基于正异性基础的传统低级分解法具有若干优势,其中包括保护诸如聚度或非饱和性、解释数据的能力和减少储存要求等属性。找到将剩余错误的规范降到最低的骨架的问题众所周知是NP硬的,但典型的节流方案,如专列的QR工作在实践上往往效果良好。当它与随机化的减少尺寸技术相结合时,基于典型的分流法方法变得特别有效,并证明能够非常迅速地计算大规模、潜在稀少、基数的CUR分解法。计算CUR脱位的另一种流行算法是随机地从全指数集中抽取柱和行,使用基于杠杆分数的专门概率分布法。这种基于取样的技术特别吸引了非常大规模的简化规模的简化技术,对于大规模简化的简化技术特别具有吸引力,而基于古典化的简化的精确性研究则则提供了一些最新的理论修正。