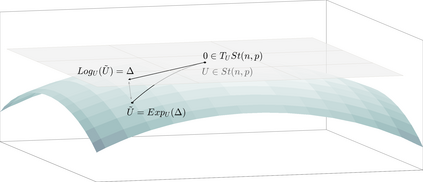
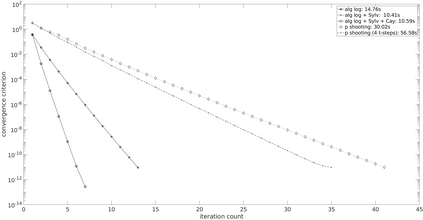
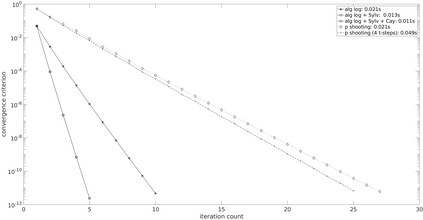
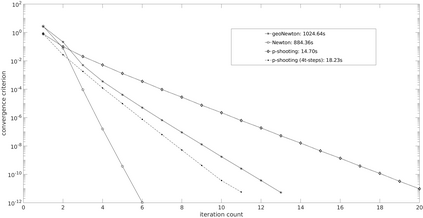
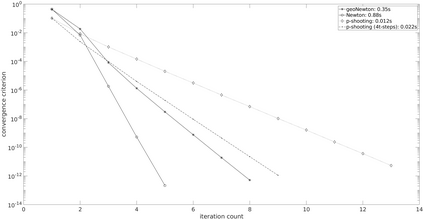
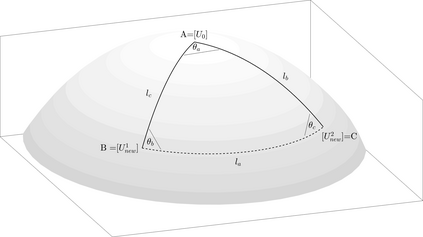
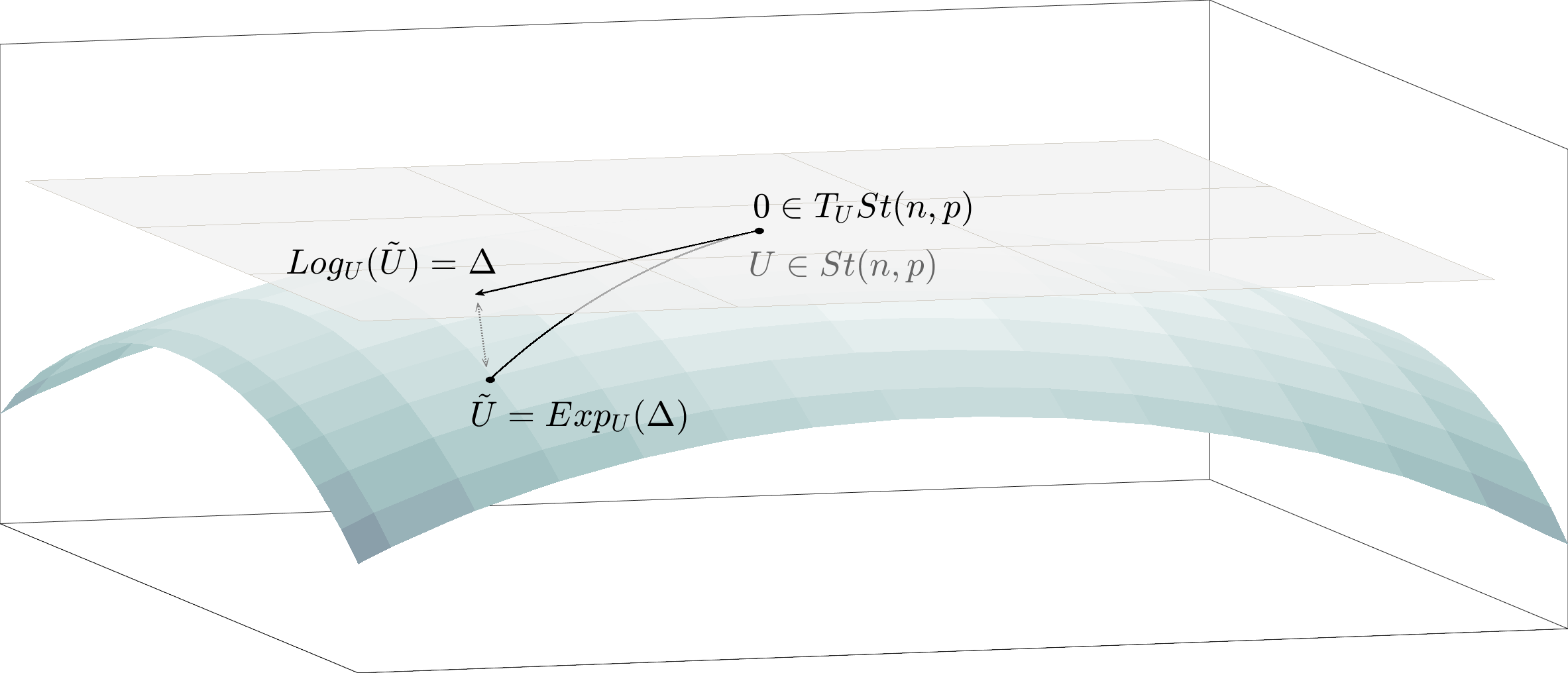
We address the problem of computing Riemannian normal coordinates on the real, compact Stiefel manifold of orthogonal frames. The Riemannian normal coordinates are based on the so-called Riemannian exponential and the Riemannian logarithm maps and enable to transfer almost any computational procedure to the realm of the Stiefel manifold. To compute the Riemannian logarithm is to solve the (local) geodesic endpoint problem. Instead of restricting the consideration to geodesics with respect to a single selected metric, we consider a family of Riemannian metrics introduced by H\"uper, Markina and Silva-Leite that includes the Euclidean and the canonical metric as prominent examples. As main contributions, we provide (1) a unified, structured, reduced formula for the Stiefel geodesics for the complete family of metrics, (2) a unified method to tackle the geodesic endpoint problem, (3) an improvement of the existing Riemannian log map under the canonical metric. The findings are illustrated by means of numerical examples, where the novel algorithms prove to be the most efficient methods known to this date.
翻译:我们解决了在正方形实际的紧凑 Stiefel 方块上计算里曼尼正常坐标的问题。里曼尼正常坐标以所谓的里曼指数和里曼尼对数地图为基础,能够将几乎任何计算程序转移到斯特杰尔方块的范围。计算里曼尼对数是解决(当地)大地学终点问题的统一方法。我们不把考虑限于对单一选定度量计的大地测量学,而是考虑H\"uper、Markina和Silva-Leite所介绍的里曼度量度数家庭,其中包括Euclidean和Canonical度量度图,作为突出的例子。作为主要贡献,我们提供了(1) Stiefel大地学公式的统一、结构化和减少公式,用于整个度量度组,(2)解决地德端点问题的统一方法,(3)改进目前Riemannian对地标图,在卡度度度度测量中采用的方法。研究结果通过数字示例加以说明,其中新颖的算法证明这一有效日期。