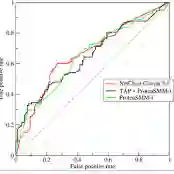
Probability forecasts for binary outcomes, often referred to as probabilistic classifiers or confidence scores, are ubiquitous in science and society, and methods for evaluating and comparing them are in great demand. We propose and study a triptych of diagnostic graphics that focus on distinct and complementary aspects of forecast performance: The reliability diagram addresses calibration, the receiver operating characteristic (ROC) curve diagnoses discrimination ability, and the Murphy diagram visualizes overall predictive performance and value. A Murphy curve shows a forecast's mean elementary scores, including the widely used misclassification rate, and the area under a Murphy curve equals the mean Brier score. For a calibrated forecast, the reliability curve lies on the diagonal, and for competing calibrated forecasts, the ROC and Murphy curves share the same number of crossing points. We invoke the recently developed CORP (Consistent, Optimally binned, Reproducible, and Pool-Adjacent-Violators (PAV) algorithm based) approach to craft reliability diagrams and decompose a mean score into miscalibration (MCB), discrimination (DSC), and uncertainty (UNC) components. Plots of the DSC measure of discrimination ability versus the calibration metric MCB visualize classifier performance across multiple competitors. The proposed tools are illustrated in empirical examples from astrophysics, economics, and social science.
翻译:对二进制结果的概率预测,通常被称为概率分类或信心分数,在科学和社会上是无处不在的,评估和比较的方法非常需要。我们提出并研究三进诊断图,侧重于预测业绩的不同和互补方面。我们提出并研究三进诊断图,侧重于预测业绩的不同和互补方面。可靠性图表校准、接收器操作特征曲线(ROC)诊断歧视能力以及墨菲图直观地反映了总体预测性能和价值。墨菲曲线显示预测的平均基本分数,包括广泛使用的错误分类率,而墨菲曲线下的区域等于平均布里尔分数。对于校准的预测来说,可靠性曲线位于对角线上,对相互竞争的校准预测来说,ROC和墨菲曲线共享相同的过境点数。我们引用最近开发的CORP(C(Conisticent, Apressly binne,Reproduction,Reportial) 和pool-Ajectration-victor (PAV) 算法方法,用来绘制可靠性图表和将平均分数分数误算法(MCB), 校正化分析/C) 标准工具的不确定性和MC。