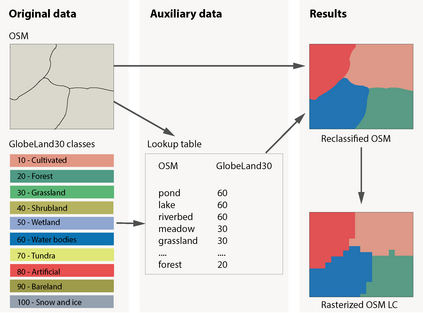
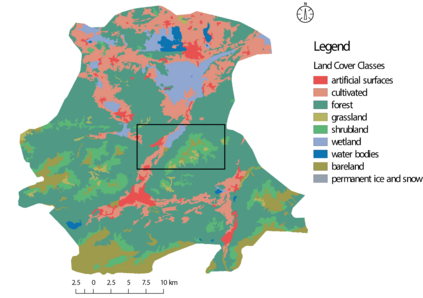
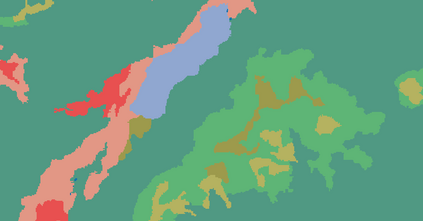
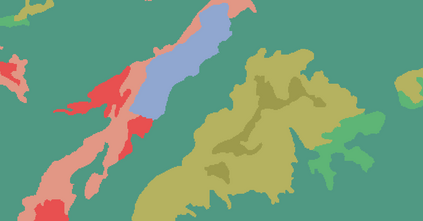
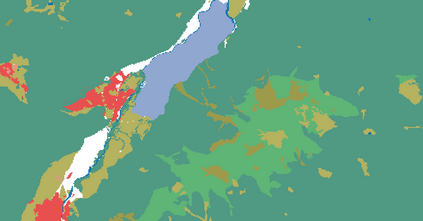
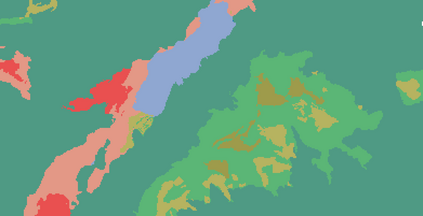
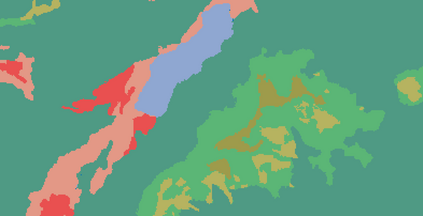
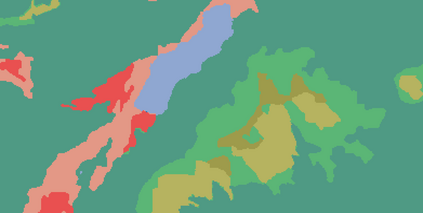
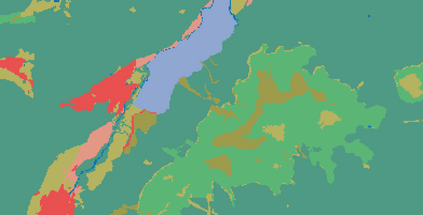
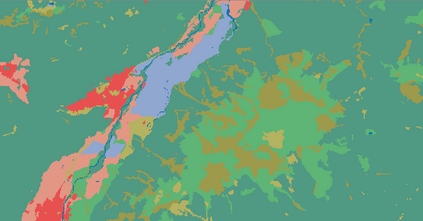
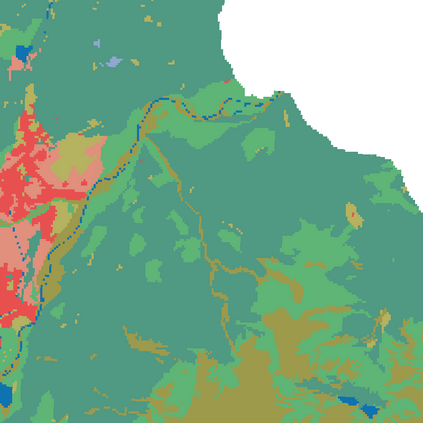
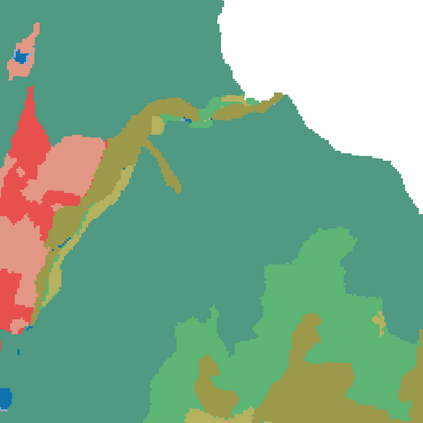
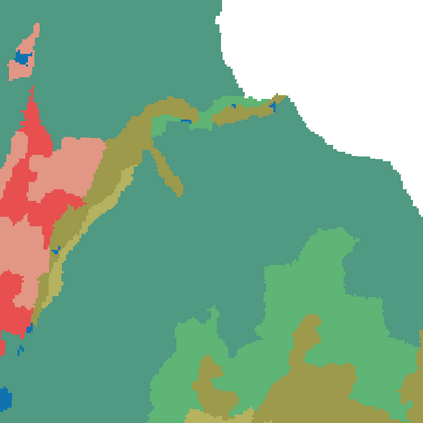
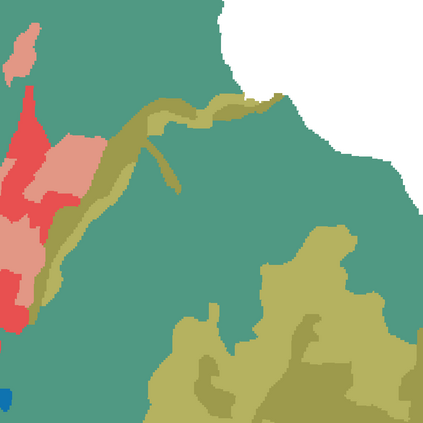
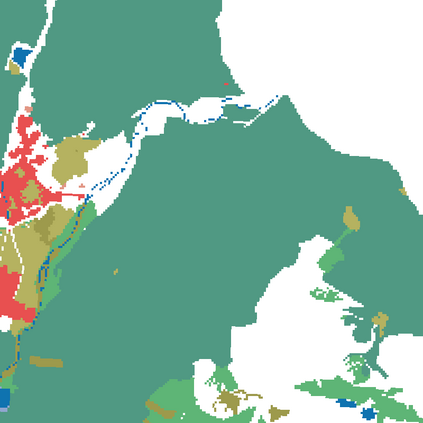
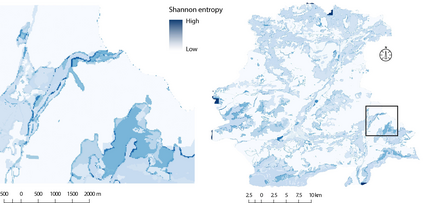
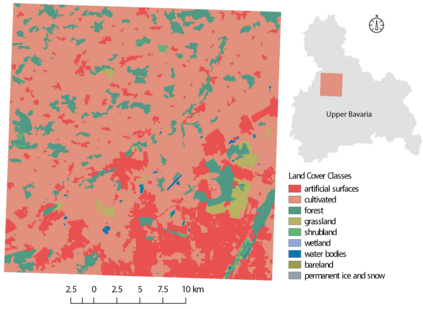
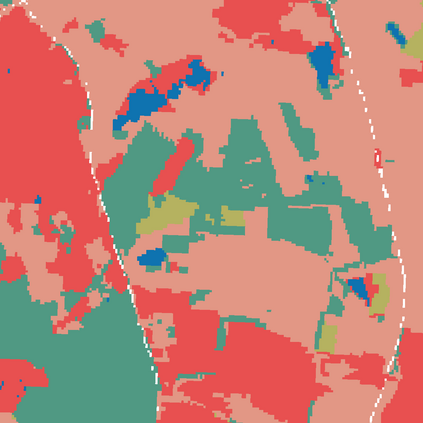
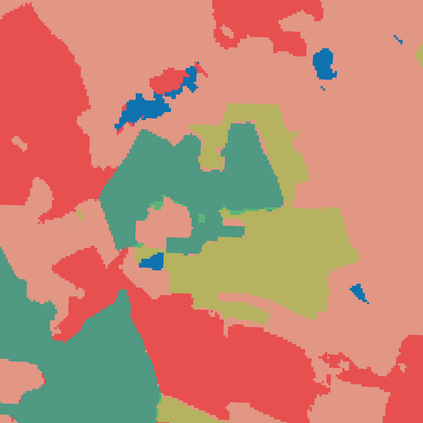
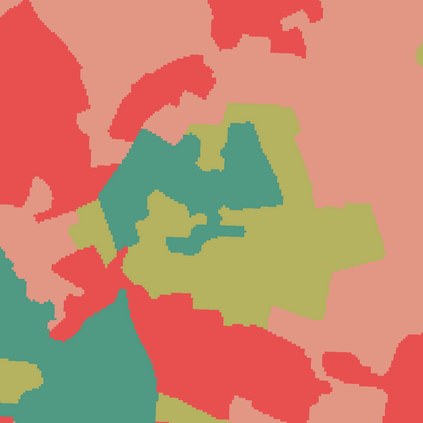
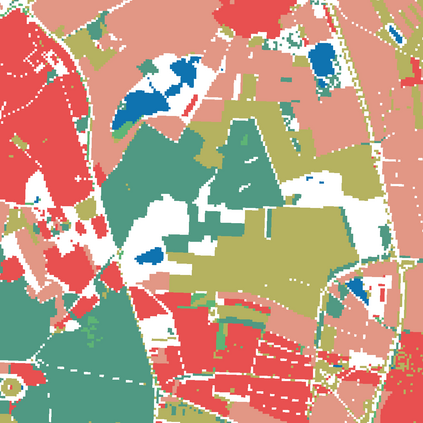
Probabilistic graphical models (PGMs) are tools for solving complex probabilistic relationships. However, suboptimal PGM structures are primarily used in practice. This dissertation presents three contributions to the PGM literature. The first is a comparison between factor graphs and cluster graphs on graph colouring problems such as Sudokus - indicating a significant advantage for preferring cluster graphs. The second is an application of cluster graphs to a practical problem in cartography: land cover classification boosting. The third is a PGMs formulation for constraint satisfaction problems and an algorithm called purge-and-merge to solve such problems too complex for traditional PGMs.
翻译:概率图形模型(PGMs)是解决复杂概率关系的工具。然而,亚最佳的PGM结构主要用于实践。该论文为PGM文献提供了三种贡献。第一,在Sudokos等图形颜色问题的系数图和群集图之间进行比较,表明更喜欢群集图的优势。第二,将群集图应用于制图中的一个实际问题:土地覆盖分类的增强。第三,对制约满意度问题的PGMs配方和一种称为清洗和合并的算法,以解决传统PGM过于复杂的这类问题。