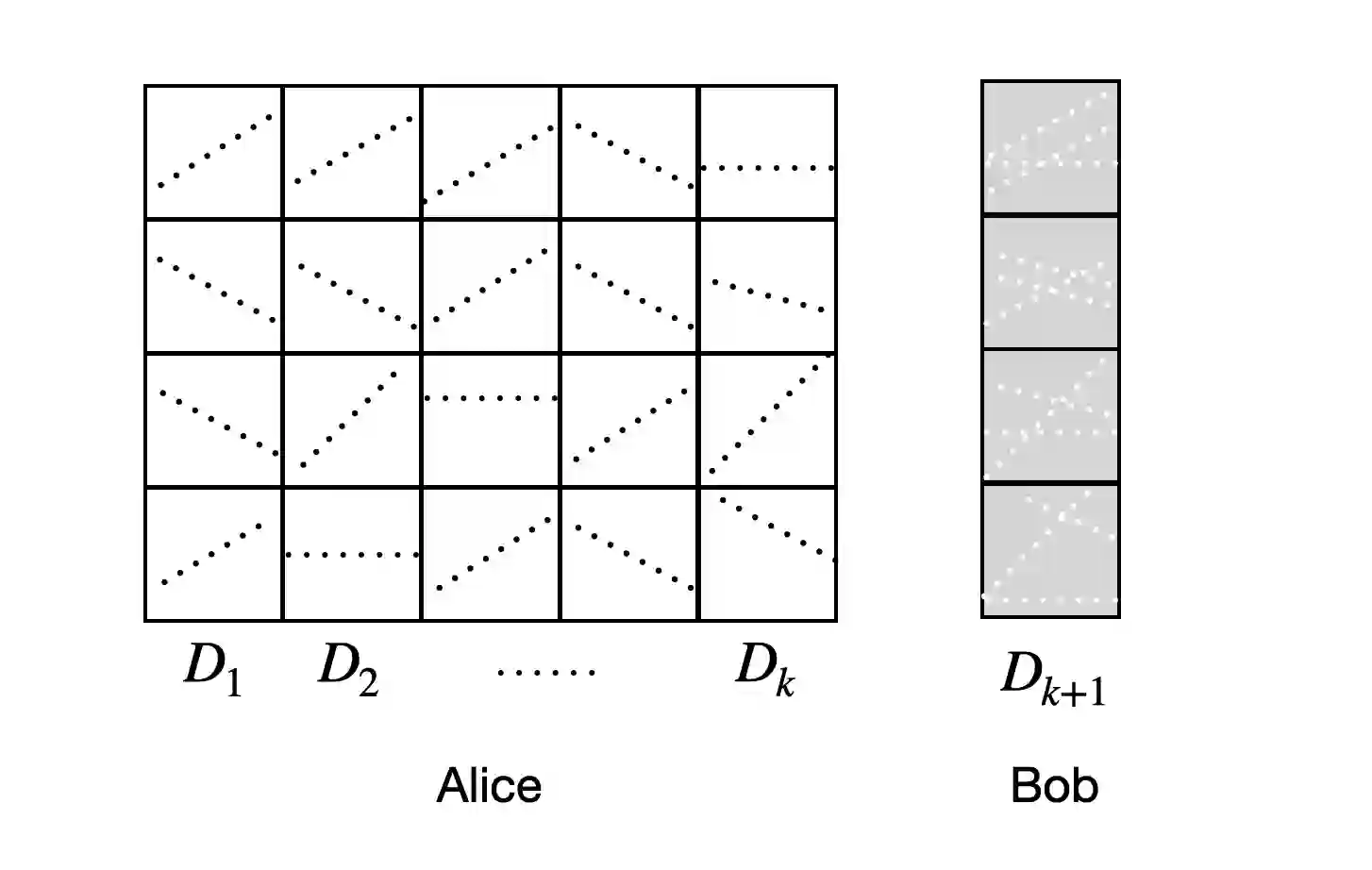
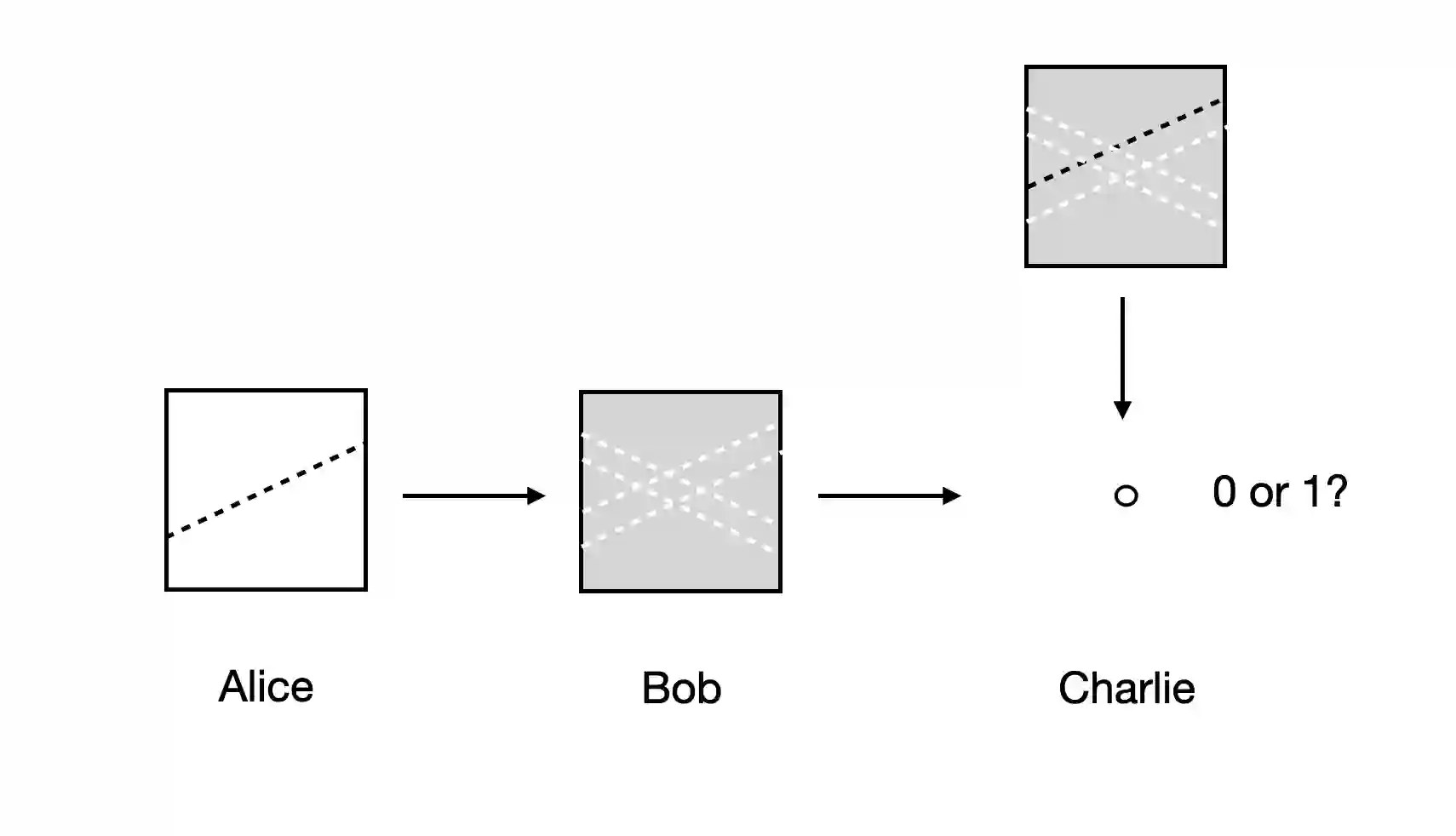
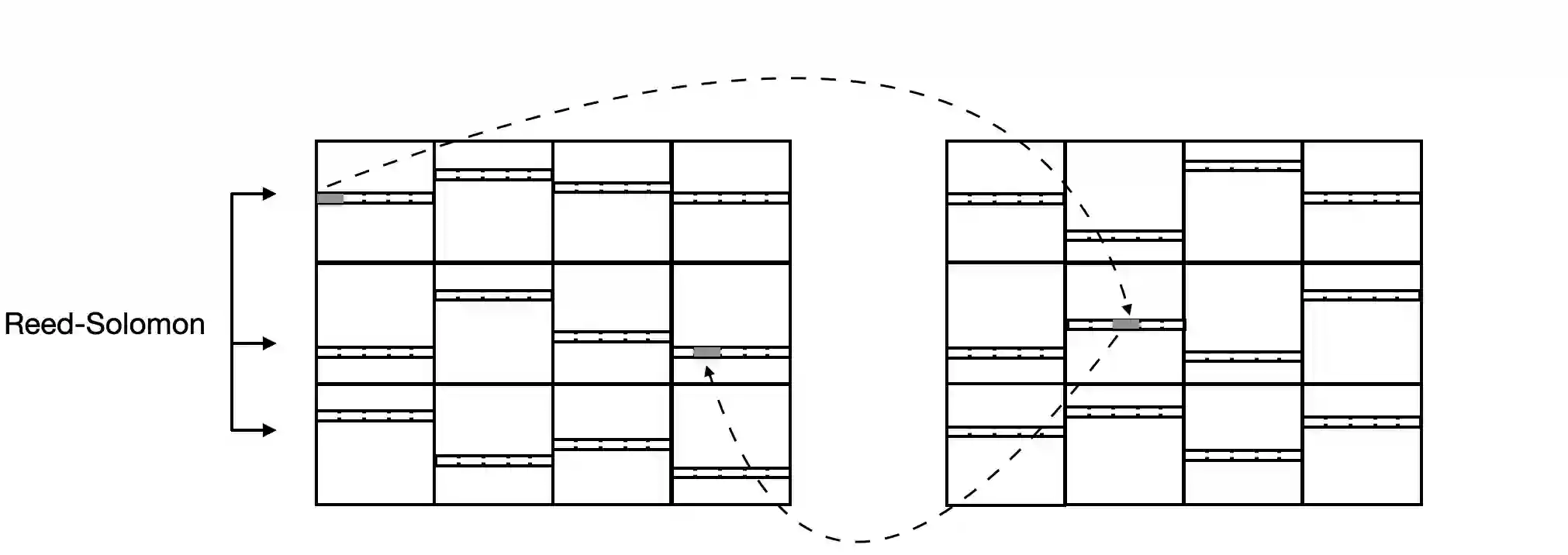
Continual learning, or lifelong learning, is a formidable current challenge to machine learning. It requires the learner to solve a sequence of $k$ different learning tasks, one after the other, while retaining its aptitude for earlier tasks; the continual learner should scale better than the obvious solution of developing and maintaining a separate learner for each of the $k$ tasks. We embark on a complexity-theoretic study of continual learning in the PAC framework. We make novel uses of communication complexity to establish that any continual learner, even an improper one, needs memory that grows linearly with $k$, strongly suggesting that the problem is intractable. When logarithmically many passes over the learning tasks are allowed, we provide an algorithm based on multiplicative weights update whose memory requirement scales well; we also establish that improper learning is necessary for such performance. We conjecture that these results may lead to new promising approaches to continual learning.
翻译:持续学习或终身学习是当前对机器学习的艰巨挑战。 它要求学习者解决一系列不同的学习任务,一个接一个地解决不同的学习任务,同时保留其早期任务的能力; 不断学习者的规模应该比为每项任务开发和保持一个单独的学习者的明显解决办法要大得多。 我们开始在PAC框架内对持续学习进行复杂理论研究。 我们用新的通信复杂性来确定,任何不断学习者,即使是不适当的学习者,都需要以美元线性增长的记忆,这强烈地表明这个问题是难以解决的。 当逻辑性地说,许多学习任务通过时,我们提供一种基于多倍增权重更新的算法,其记忆要求尺度也很好; 我们还确定,不适当的学习对于这种学习是必要的。 我们推测,这些结果可能导致新的有希望的继续学习方法。
相关内容
Source: Apple - iOS 8