Fairness for AUC via Feature Augmentation

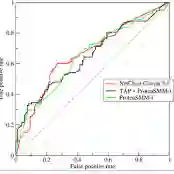
We study fairness in the context of classification where the performance is measured by the area under the curve (AUC) of the receiver operating characteristic. AUC is commonly used when both Type I (false positive) and Type II (false negative) errors are important. However, the same classifier can have significantly varying AUCs for different protected groups and, in real-world applications, it is often desirable to reduce such cross-group differences. We address the problem of how to select additional features to most greatly improve AUC for the disadvantaged group. Our results establish that the unconditional variance of features does not inform us about AUC fairness but class-conditional variance does. Using this connection, we develop a novel approach, fairAUC, based on feature augmentation (adding features) to mitigate bias between identifiable groups. We evaluate fairAUC on synthetic and real-world (COMPAS) datasets and find that it significantly improves AUC for the disadvantaged group relative to benchmarks maximizing overall AUC and minimizing bias between groups.