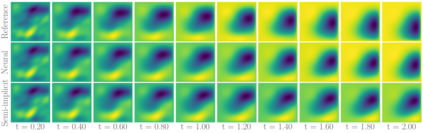
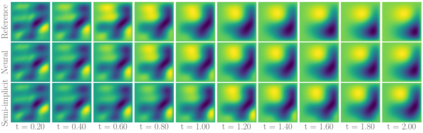
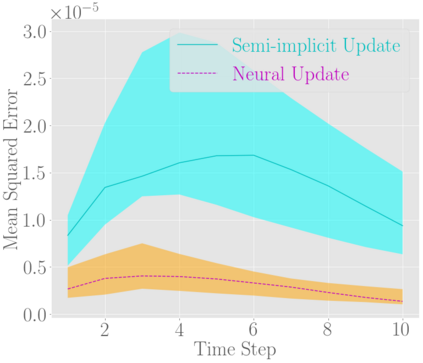
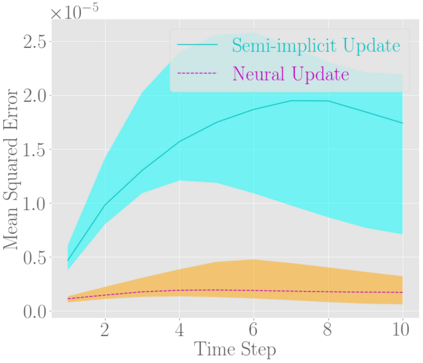
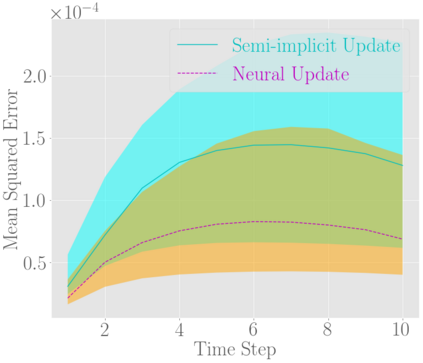
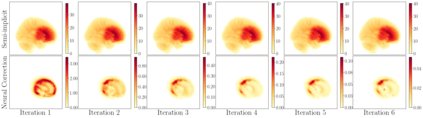
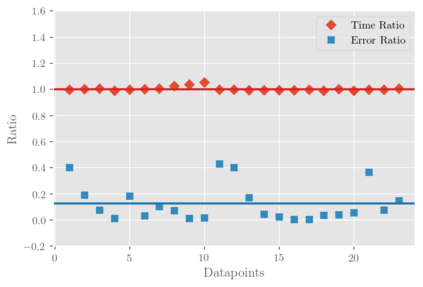
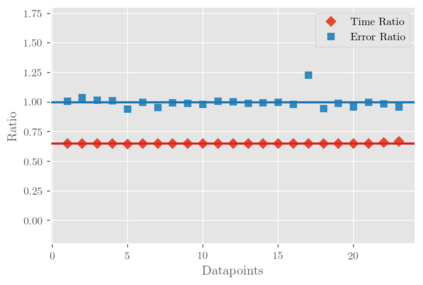
Fast and accurate solutions of time-dependent partial differential equations (PDEs) are of pivotal interest to many research fields, including physics, engineering, and biology. Generally, implicit/semi-implicit schemes are preferred over explicit ones to improve stability and correctness. However, existing semi-implicit methods are usually iterative and employ a general-purpose solver, which may be sub-optimal for a specific class of PDEs. In this paper, we propose a neural solver to learn an optimal iterative scheme in a data-driven fashion for any class of PDEs. Specifically, we modify a single iteration of a semi-implicit solver using a deep neural network. We provide theoretical guarantees for the correctness and convergence of neural solvers analogous to conventional iterative solvers. In addition to the commonly used Dirichlet boundary condition, we adopt a diffuse domain approach to incorporate a diverse type of boundary conditions, e.g., Neumann. We show that the proposed neural solver can go beyond linear PDEs and applies to a class of non-linear PDEs, where the non-linear component is non-stiff. We demonstrate the efficacy of our method on 2D and 3D scenarios. To this end, we show how our model generalizes to parameter settings, which are different from training; and achieves faster convergence than semi-implicit schemes.
翻译:对于许多研究领域,包括物理学、工程学和生物学,对物理、工程学和生物学等许多研究领域来说,对基于时间的局部偏差方程(PDEs)至关重要的快速和准确的解决方案。一般而言,为了提高稳定性和正确性,隐含/半隐含计划优于显性计划。然而,现有的半隐含方法通常是迭接的,并使用通用的解答器,对于某类PDEs来说,它可能是亚最佳的。在本文中,我们建议一个神经解答器,以数据驱动的方式为任何一类PDEs学习一个最佳的迭接机制。具体地说,我们用深神经网络来修改一个半隐含的解析器的单一代谢。我们为类似于常规迭接合解答器的神经解析器提供了理论保证。除了常用的Drichlet边界条件外,我们还采用一种分散的域处理法,将不同的边界条件,例如Neumann。我们表明,拟议的神经解解解解解解器可以超越任何一类非线式PDES,并适用于非线式的解解解解解解解解解解解解器。 我们的图2的图3-Dreal-deal-dealental-deplic-degradustris-degradustrut-destrucaliz-dealiz-toxx