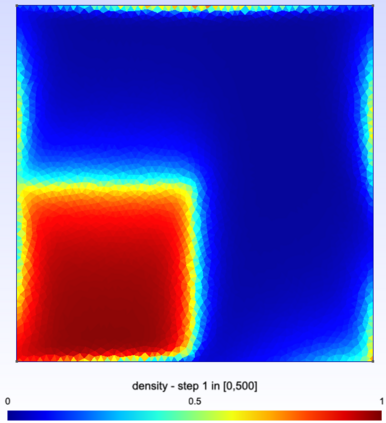
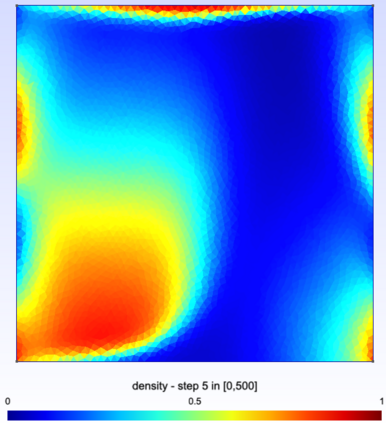
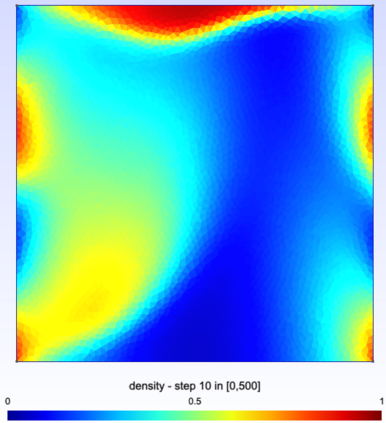
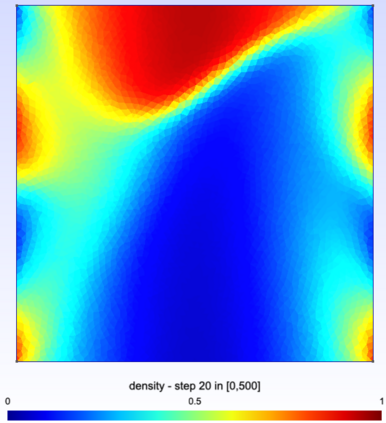
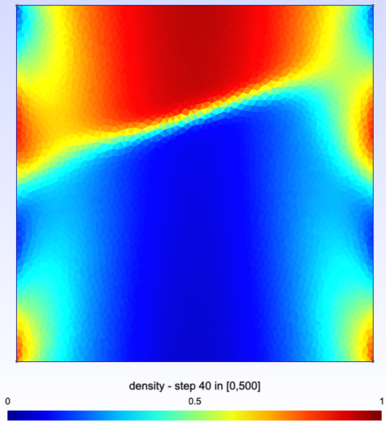
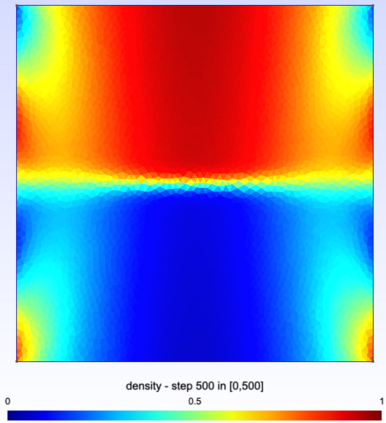
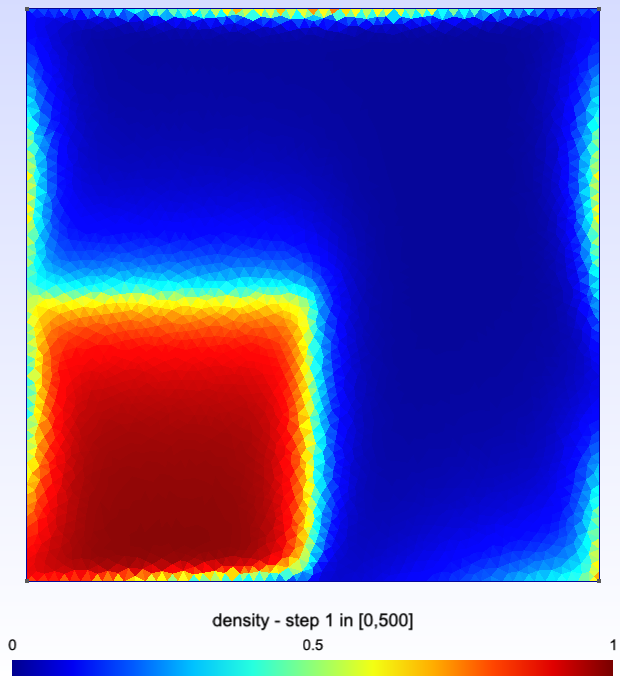
We study a finite volume scheme for the approximation of the solution to convection diffusion equations with nonlinear convection and Robin boundary conditions. The scheme builds on the interpretation of such a continuous equation as the hydrodynamic limit of some simple exclusion jump process. We show that the scheme admits a unique discrete solution, that the natural bounds on the solution are preserved, and that it encodes the second principle of thermodynamics in the sense that some free energy is dissipated along time. The convergence of the scheme is then rigorously established thanks to compactness arguments. Numerical simulations are finally provided, highlighting the overall good behavior of the scheme.
翻译:我们研究一个数量有限的办法,以近似于非线性对流和罗宾边界条件的对流扩散方程式。这个办法基于对诸如某些简单的排除跳动过程的流体动力极限等连续方程式的解释。我们表明,这个办法承认了一种独特的离散解决办法,解决办法的自然界限得到了维护,它将热力学的第二项原则编码为某种自由能量随时间消散。然后,由于紧凑性的论点,这个办法的趋同得到了严格确立。最后提供了数字模拟,突出了这个办法的总体良好行为。