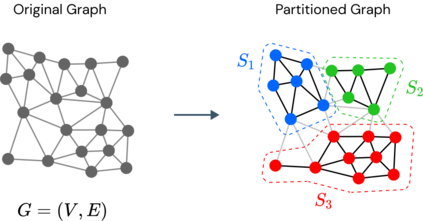
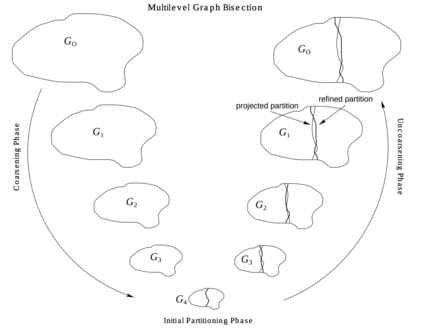
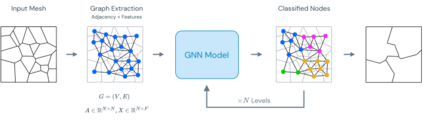
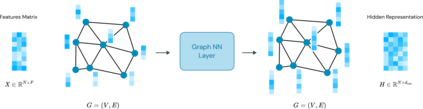
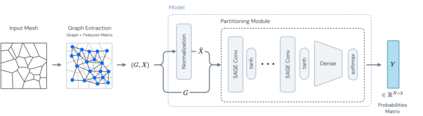
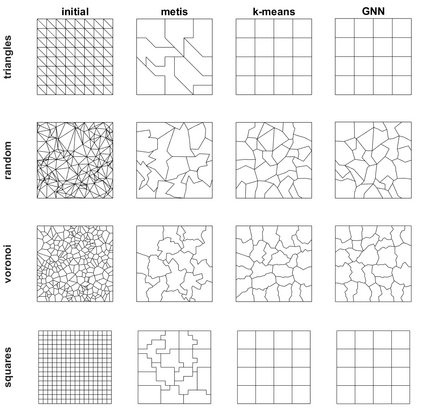
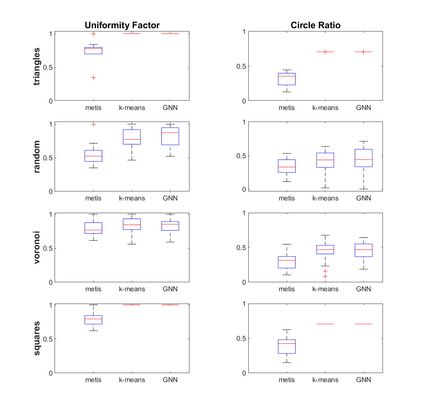
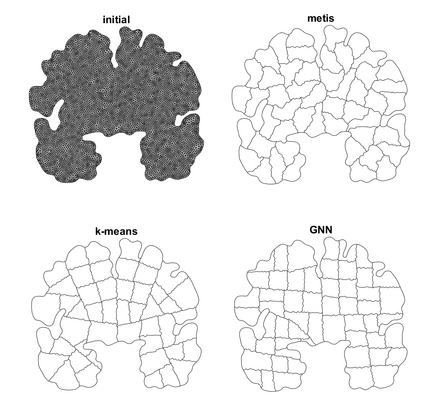
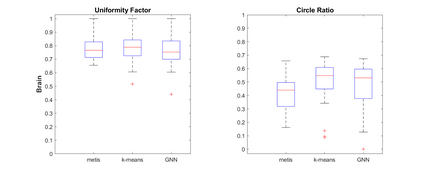
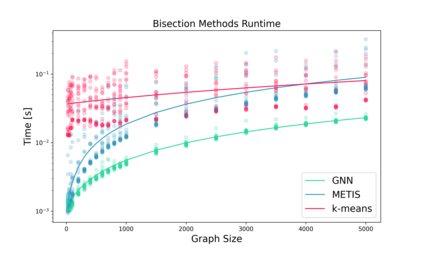
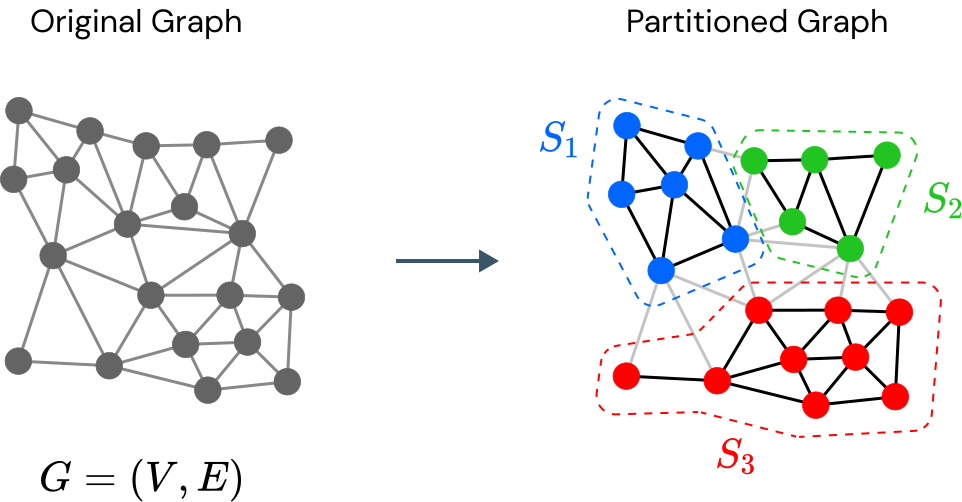
Agglomeration-based strategies are important both within adaptive refinement algorithms and to construct scalable multilevel algebraic solvers. In order to automatically perform agglomeration of polygonal grids, we propose the use of Graph Neural Networks (GNNs) to partition the connectivity graph of a computational mesh. GNNs have the advantage to process naturally and simultaneously both the graph structure of mesh and the geometrical information, such as the areas of the elements or their barycentric coordinates. This is not the case with other approaches such as METIS, a standard algorithm for graph partitioning which is meant to process only the graph information, or the k-means clustering algorithm, which can process only the geometrical information. Performance in terms of quality metrics is enhanced for Machine Learning (ML) strategies, with GNNs featuring a lower computational cost online. Such models also show a good degree of generalization when applied to more complex geometries, such as brain MRI scans, and the capability of preserving the quality of the grid. The effectiveness of these strategies is demonstrated also when applied to MultiGrid (MG) solvers in a Polygonal Discontinuous Galerkin (PolyDG) framework.
翻译:以聚合为基础的战略在适应性改进算法和构建可缩放的多级代数求解器中都很重要。为了自动执行多边形网格的组合化,我们提议使用图形神经网络(GNNS)来分隔计算网格的连接图。 GNNS具有自然和同时处理网格图结构和几何信息图结构的优势,如元素区域或其粗心坐标。其他方法,如METIS, 用于图形分割的标准算法,仅用于处理图形信息,或K- means群集算法,仅处理几何信息。机械学习战略的质量指标性能得到加强,而GNNS的计算成本在线成本较低。这些模型还表明,在应用于更复杂的地理比例方面,例如脑 MRI 扫描, 和维护电网格质量的能力等,具有相当程度的概括性。这些战略的有效性在应用多基调调调调(Disgal Contal)框架时,也表现了。