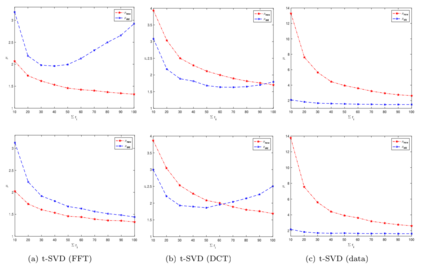
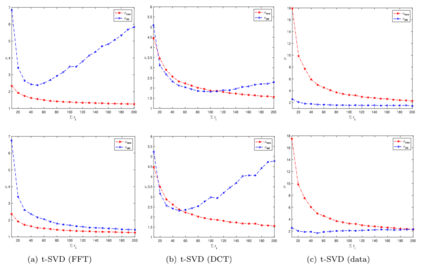
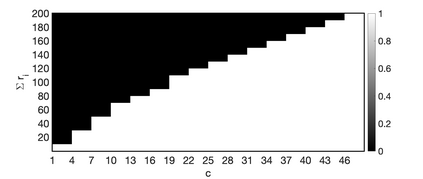
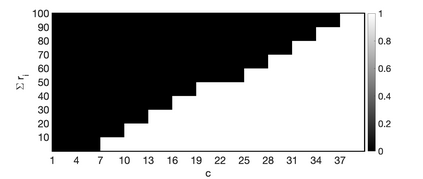
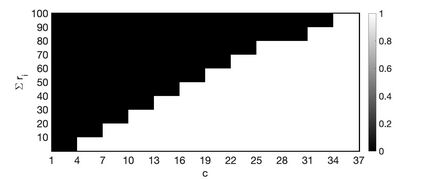
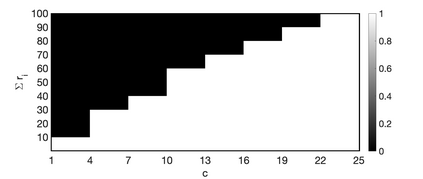
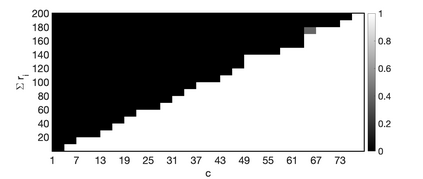
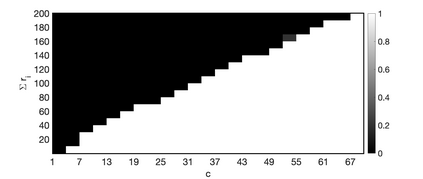
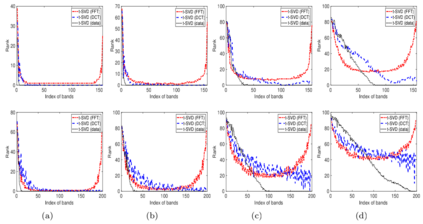
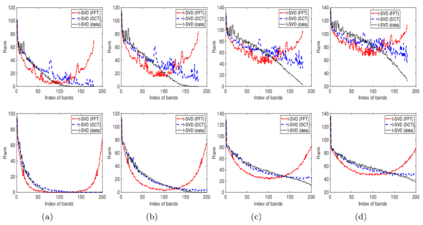
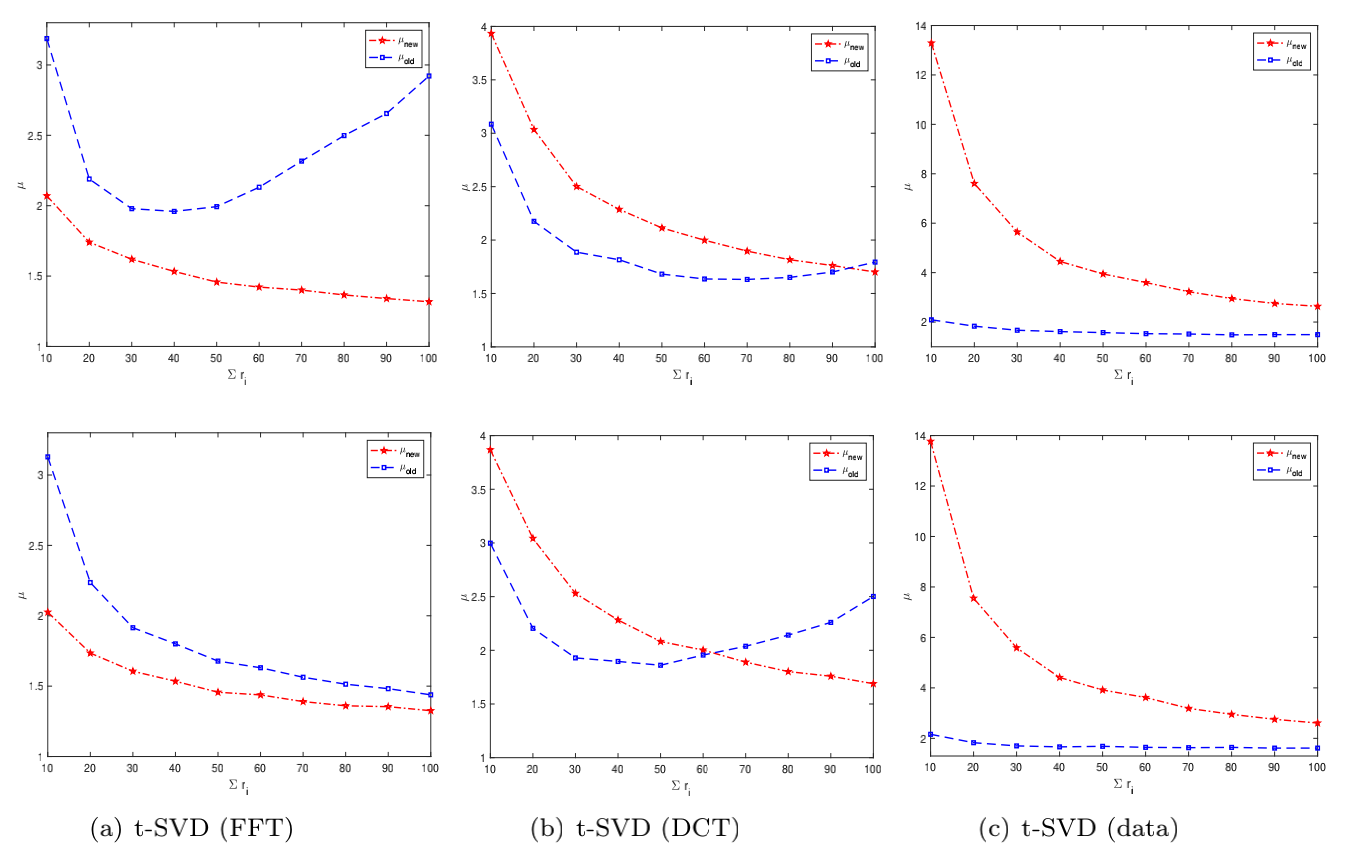
One of the key problems in tensor completion is the number of uniformly random sample entries required for recovery guarantee. The main aim of this paper is to study $n_1 \times n_2 \times n_3$ third-order tensor completion and investigate into incoherence conditions of $n_3$ low-rank $n_1$-by-$n_2$ matrix slices under the transformed tensor singular value decomposition where the unitary transformation is applied along $n_3$-dimension. We show that such low-rank tensors can be recovered exactly with high probability when the number of randomly observed entries is of order $O( r\max \{n_1, n_2 \} \log ( \max \{ n_1, n_2 \} n_3))$, where $r$ is the sum of the ranks of these $n_3$ matrix slices in the transformed tensor. By utilizing synthetic data and imaging data sets, we demonstrate that the theoretical result can be obtained under valid incoherence conditions, and the tensor completion performance of the proposed method is also better than that of existing methods in terms of sample sizes requirement.
翻译:单项变换在单项变换在单项变换中应用的单项变换单项变换值的总和中,在变变换成单项变换时,美元是美元1美元1美元1美元1美元1美元1美元1美元2美元2美元基质切片,在变换成单项变换在变换后,单项变换在变换时采用单项变换值1美元3美元的基质切片,因此,在随机观察到的分录数量为美元O(r\max n_1美元1美元、n_2美元)时,本文件的主要目的是研究3美元第三顺序的补全和调查不一致性条件(nxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx)xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx