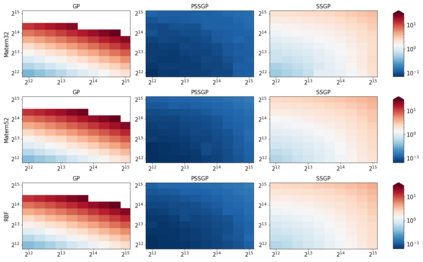
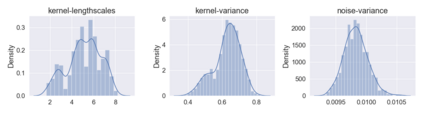
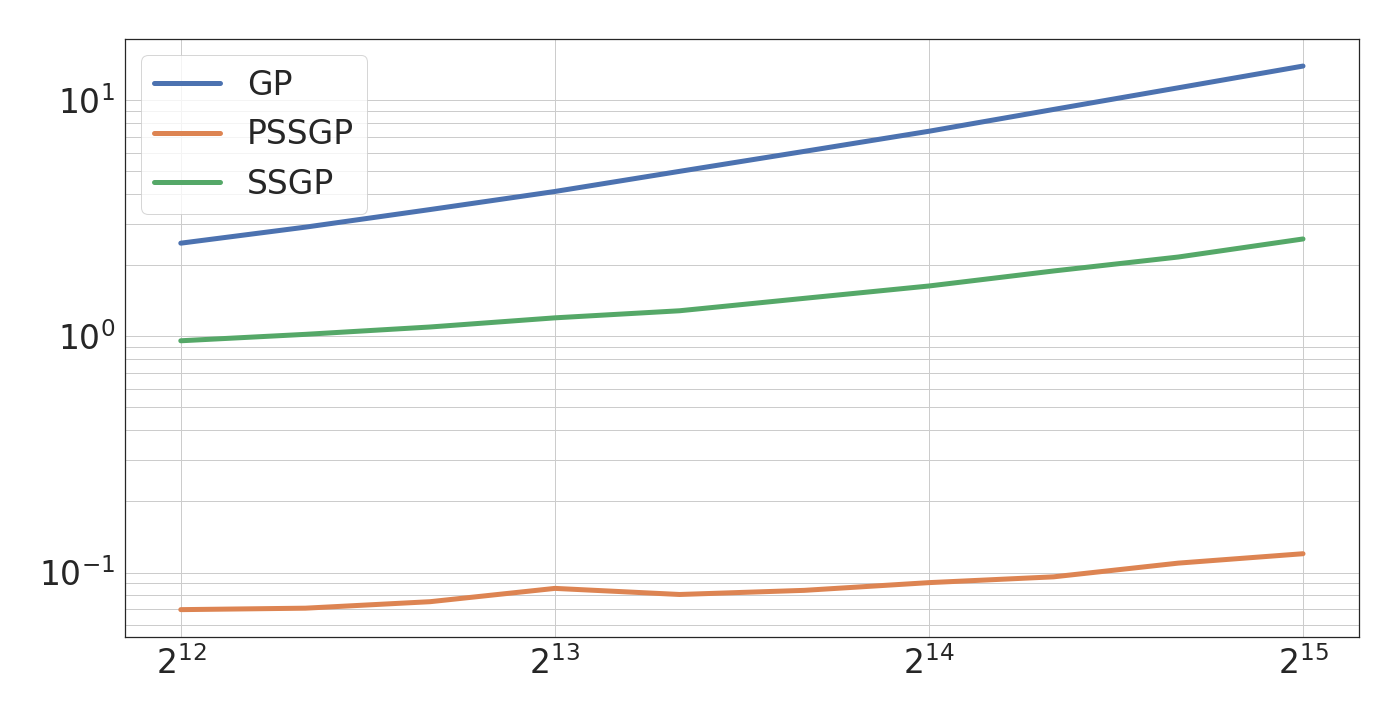
The aim of this article is to present a novel parallelization method for temporal Gaussian process (GP) regression problems. The method allows for solving GP regression problems in logarithmic $O(\log N)$ time, where $N$ is the number of time steps. Our approach uses the state-space representation of GPs which in its original form allows for linear $O(N)$ time GP regression by leveraging the Kalman filtering and smoothing methods. By using a recently proposed parallelization method for Bayesian filters and smoothers, we are able to reduce the linear computational complexity of the Kalman filter and smoother solutions to the GP regression problems into logarithmic span complexity, which transforms into logarithm time complexity when implemented in parallel hardware such as a graphics processing unit (GPU). We experimentally demonstrate the computational benefits one simulated and real datasets via our open-source implementation leveraging the GPflow framework.
翻译:本篇文章的目的是为时间高斯进程回归问题提出一种新的平行方法。 这种方法可以解决对数 $O( log N) 时间( $N) 时间( $N) 的时间( $N) ) 的 GP回归问题。 我们的方法是使用最初形式的GP 国家- 空间表示法, 利用Kalman 过滤法和平滑法, 使GP 时间回归法出现线性。 通过对Bayesian 过滤器和平滑器使用最近提议的平行方法, 我们能够减少Kalman 过滤器的线性计算复杂性, 以及将GP 回归问题平滑的解决方案转化为对数宽度复杂度( logaty space 复杂度), 当在像图形处理器( GPUP ) 这样的平行硬件中实施时, 将转换成对数时间复杂度。 我们通过利用 GPP 流量框架的开源实施, 实验地展示一个模拟和真实的数据集的计算效益。