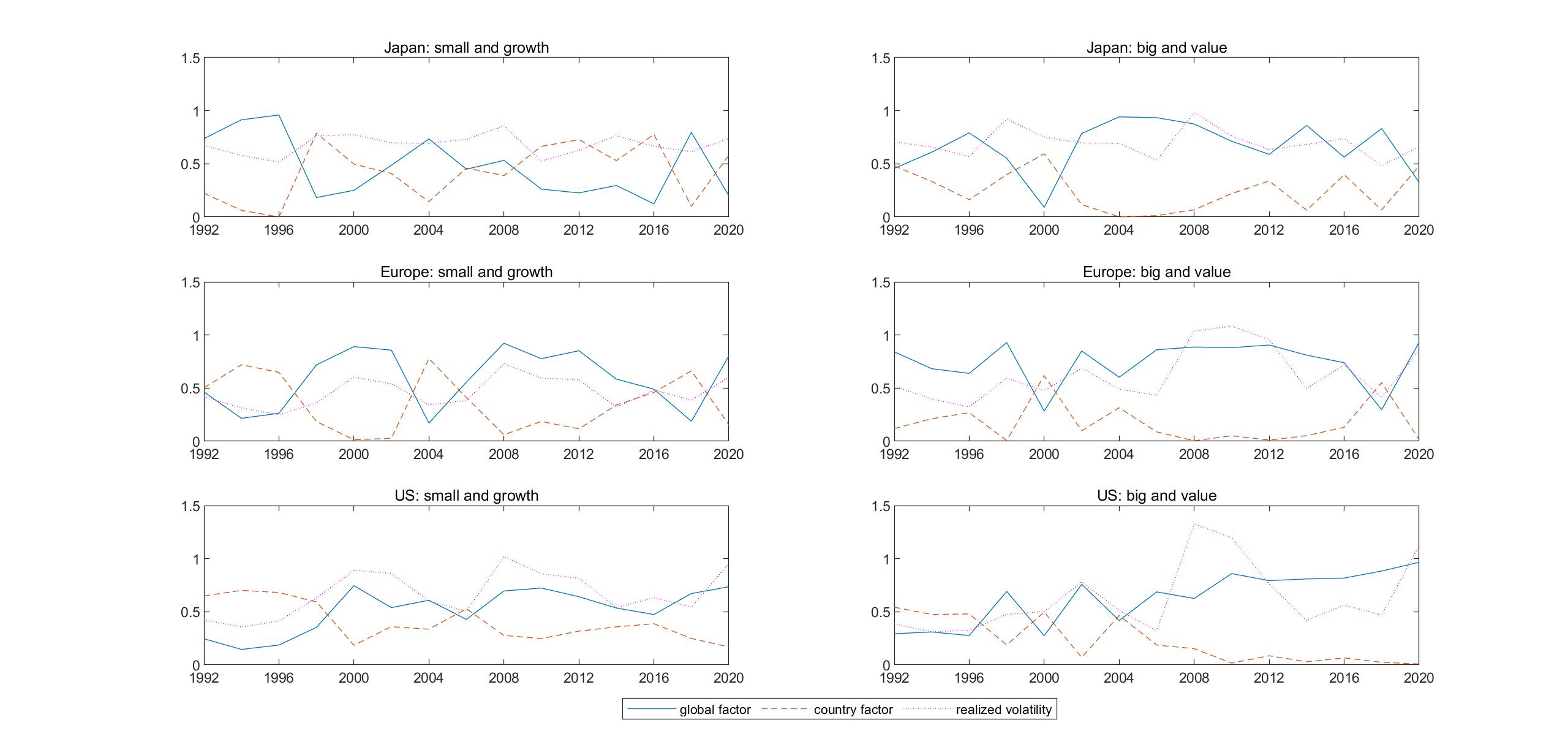
Most stock markets are open for 6-8 hours per trading day. The Asian, European and American stock markets are separated in time by time-zone differences. We propose a statistical dynamic factor model for a large number of daily returns across multiple time zones. Our model has a common global factor as well as continent factors. Under a mild fixed-signs assumption, our model is identified and has a structural interpretation. We derive the asymptotic theories of the quasi-maximum likelihood estimator (QMLE) of our model. As QMLE is inefficient by definition in this article, we outline three related estimators for practical use; Monte Carlo simulations reveal that two of them work well. We then apply our model to two real data sets - the equity portfolio returns of Japan, Europe and US and MSCI equity indices of 41 developed and emerging markets. Some new insights about linkages between different markets are drawn. Last, a Bayesian estimator (i.e., the Gibbs sampling) is also explained and suitable for estimation when the number of stocks is not too big.
翻译:多数股票市场每交易日开放6-8小时。亚洲、欧洲和美国股票市场按时区差异时间分隔。我们建议了一个统计动态因素模型,用于跨多个时区的大量每日回报。我们的模型既有共同的全球因素,也有大陆因素。在一种温和的固定标志假设下,我们的模型被确定并具有结构性解释。我们从模型的准最大可能性估测器(QMLE)中得出了无药可治理论。由于在本条中定义的QMLE是无效的,我们为实际使用概述了三个相关的估测器;蒙特卡洛模拟显示其中两个模型运作良好。我们然后将我们的模型应用于两个真实数据集,即日本、欧洲和美国的股票组合回报以及41个发达市场和新兴市场的摩根斯坦利资本国际股票指数。关于不同市场之间联系的一些新见解被绘制出来。最后,在股票数量不太大时,一个贝耶斯估计器(即Gibbs抽样)也被解释并适合估计。