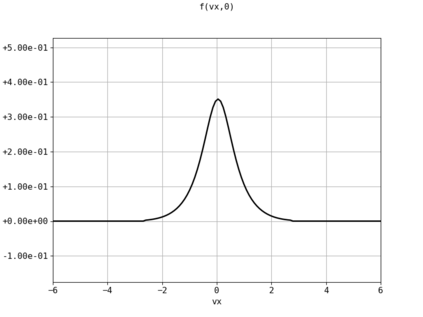
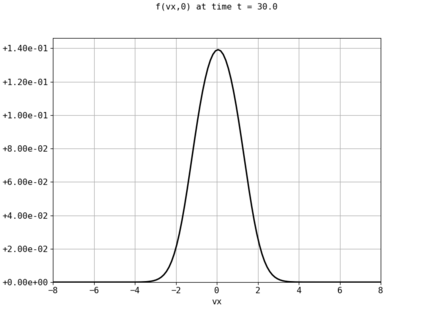
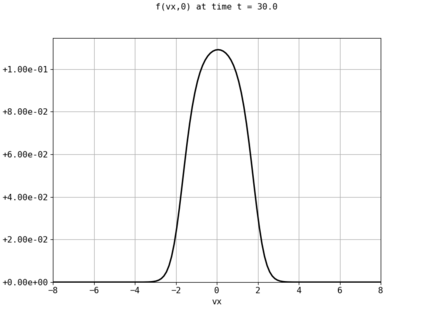
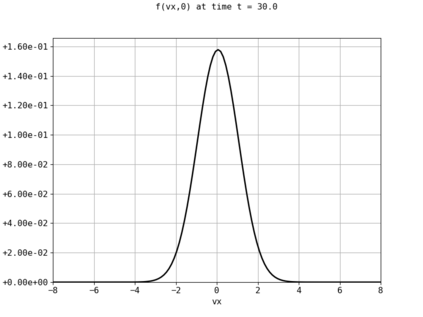
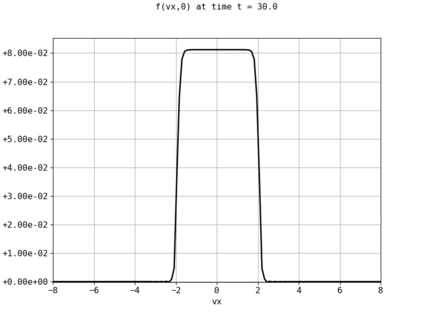
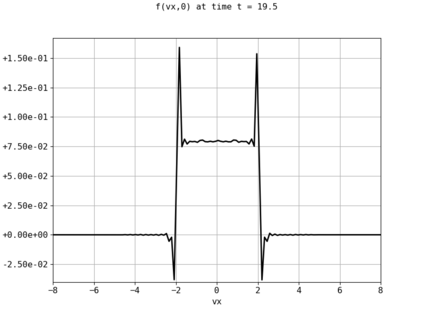
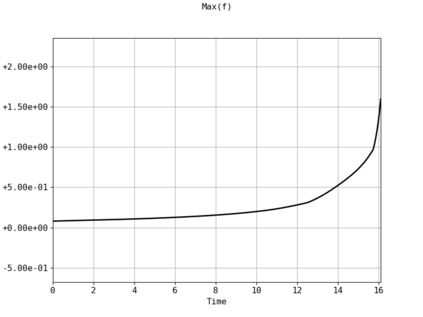
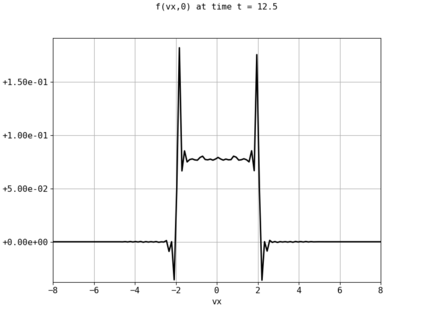
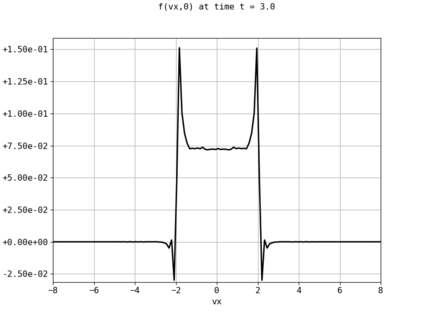
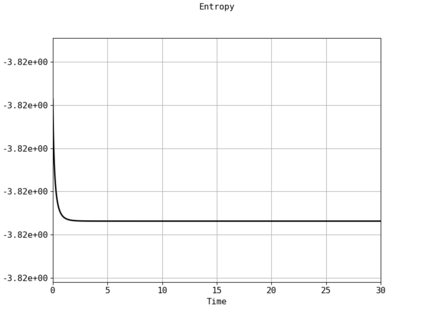
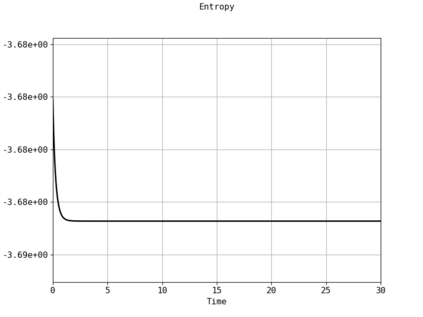
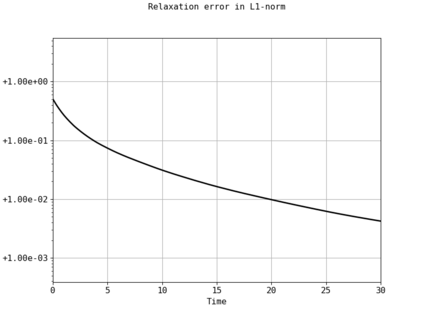
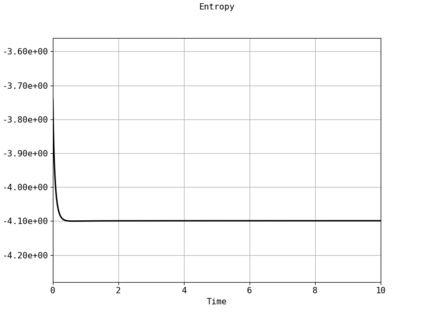
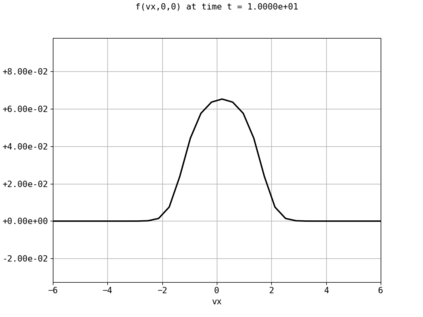
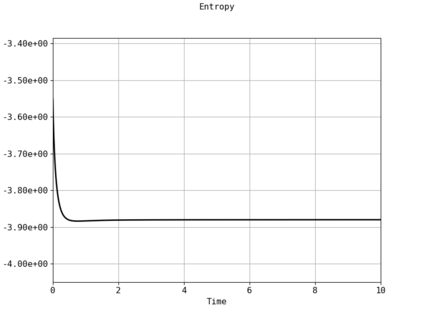
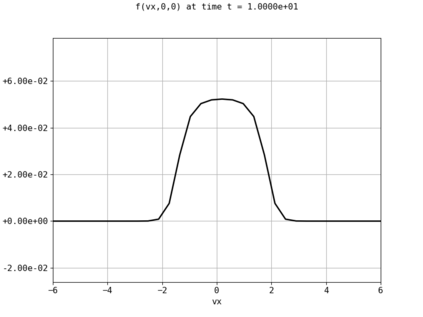
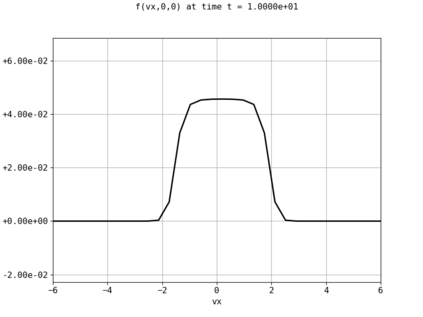
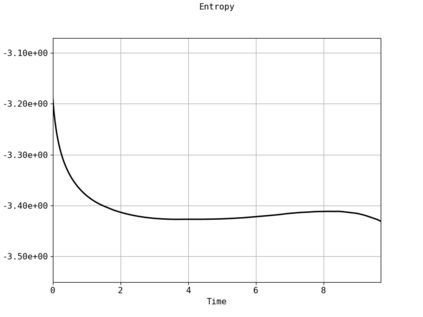
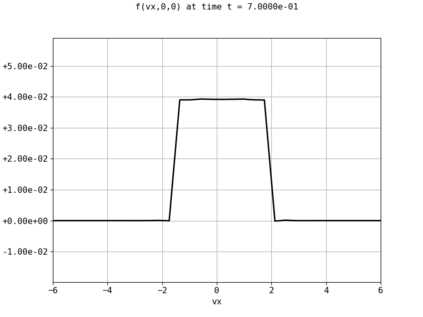
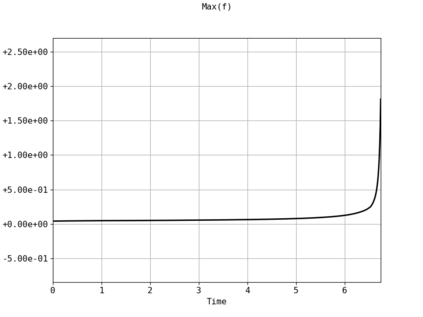
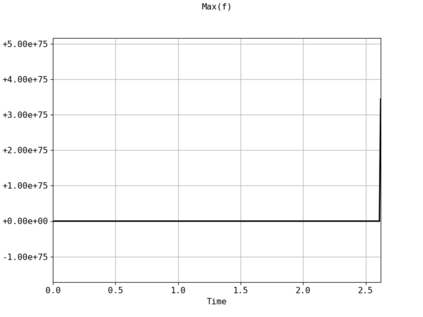
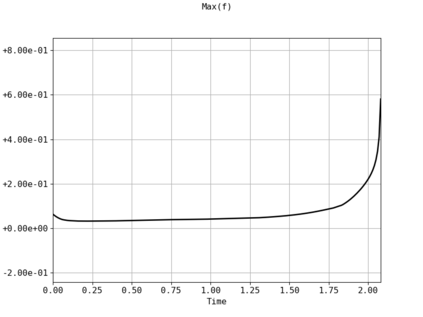
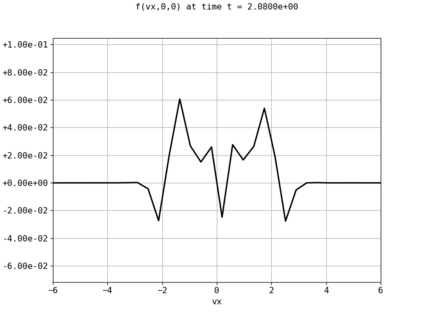
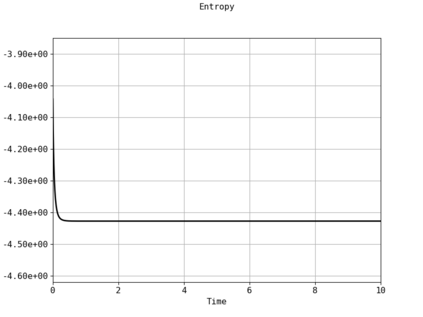
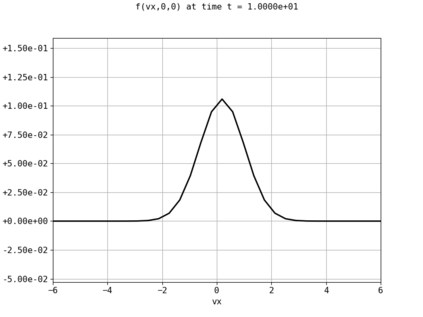
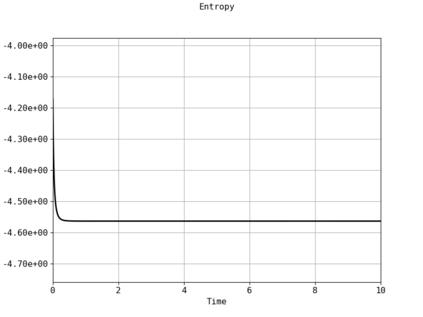
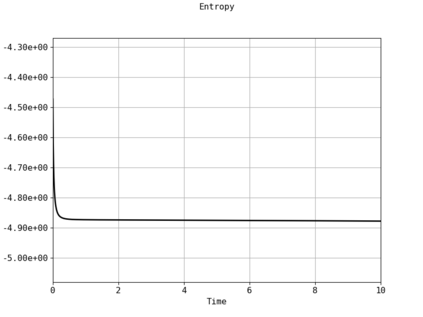
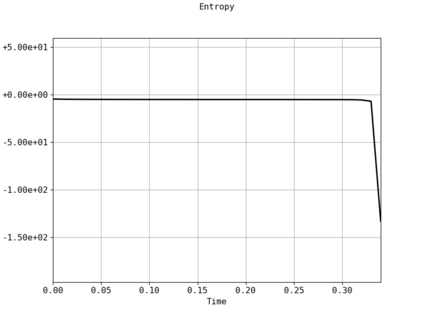
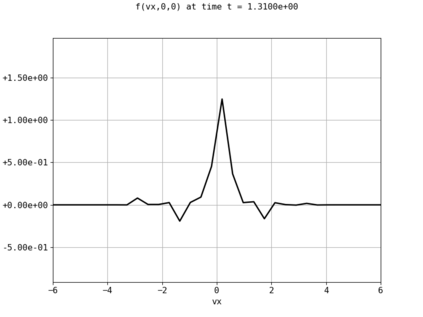
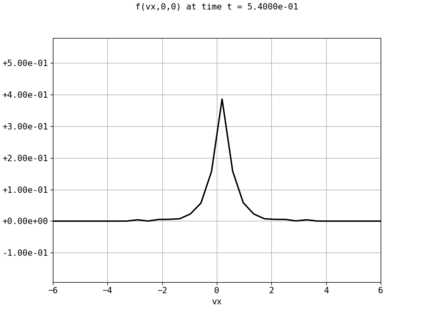
Spectral methods, thanks to their high accuracy and the possibility to use fast algorithms, represent an effective way to approximate the collisional kinetic equations of Boltzmann type, such as the Boltzmann-Nordheim equation. This equation, modeled on the seminal Boltzmann equation, describes using a statistical physics formalism the time evolution of a gas composed of bosons or fermions. Using the spectral-Galerkin algorithm introduced in [F. Filbet, J. Hu, and S. Jin, ESAIM: Math. Model. Numer. Anal., 2011], together with some novel parallelization techniques, we investigate some of the conjectured properties of the large time behavior of the solutions to this equation. In particular, we are able to observe numerically both Bose-Einstein condensation and Fermi-Dirac relaxation.
翻译:光谱方法由于其高精度和使用快速算法的可能性,是接近波尔兹曼式碰撞动能方程的有效方法,如布尔茨曼-诺德海姆方程。这个方程以原始的布尔茨曼方程为模型,用统计物理形式描述由bosons或fermions组成的气体的时间演变。使用[F. Filbet, J. Hu和S. Jin,ESAM: Math. model. Numer. Anal. 2011] 引入的光谱-伽勒金方程以及一些新型的平行技术,我们调查了这个方程的大型时间行为方法的预测属性。特别是,我们能够从数字上观察Bose-Einstein Condenation和Fermi-Dirac的放松。