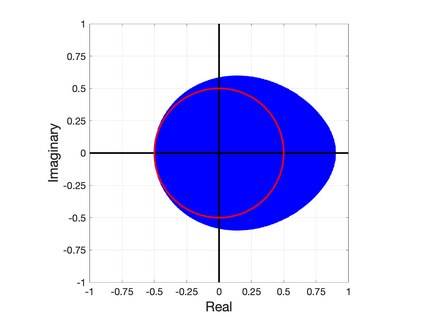
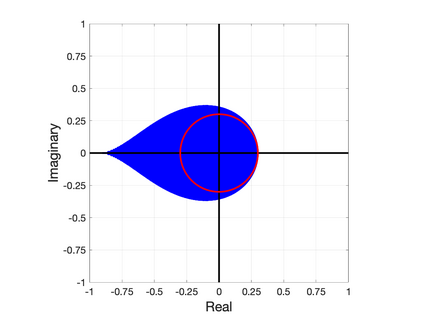
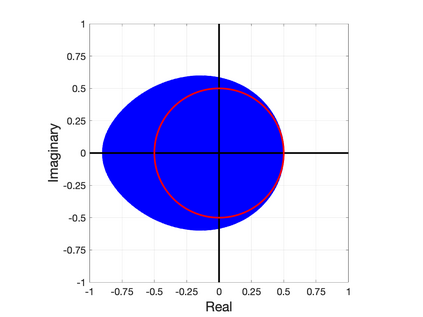
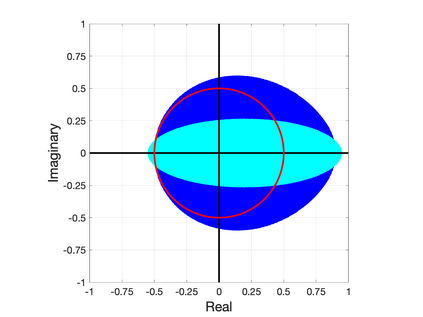
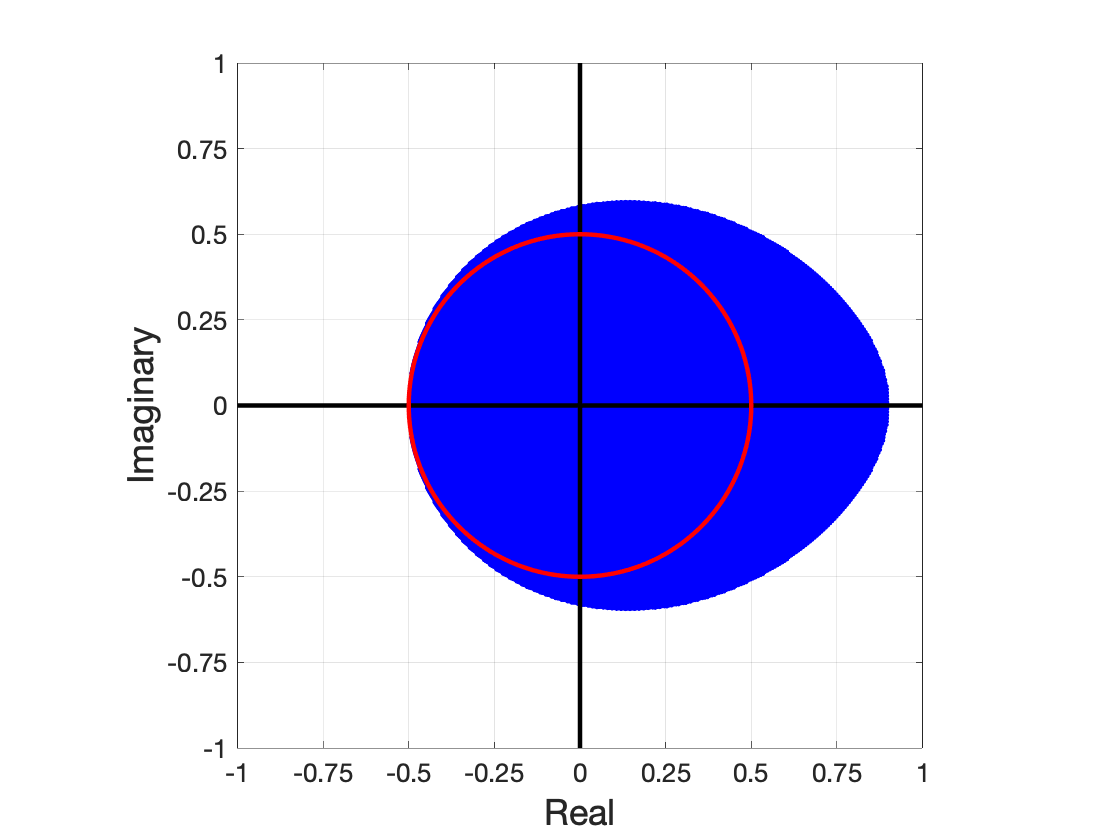
Nesterov's well-known scheme for accelerating gradient descent in convex optimization problems is adapted to accelerating stationary iterative solvers for linear systems. Compared with classical Krylov subspace acceleration methods, the proposed scheme requires more iterations, but it is trivial to implement and retains essentially the same computational cost as the unaccelerated method. An explicit formula for a fixed optimal parameter is derived in the case where the stationary iteration matrix has only real eigenvalues, based only on the smallest and largest eigenvalues. The fixed parameter, and corresponding convergence factor, are shown to maintain their optimality when the iteration matrix also has complex eigenvalues that are contained within an explicitly defined disk in the complex plane. A comparison to Chebyshev acceleration based on the same information of the smallest and largest real eigenvalues (dubbed Restricted Information Chebyshev acceleration) demonstrates that Nesterov's scheme is more robust in the sense that it remains optimal over a larger domain when the iteration matrix does have some complex eigenvalues. Numerical tests validate the efficiency of the proposed scheme. This work generalizes and extends the results of [1, Lemmas 3.1 and 3.2 and Theorem 3.3].
翻译:Nesterov 的众所周知的在螺旋优化问题中加速梯度下降的计划适应了线性系统加速的固定迭代求解器。 与古典的 Krylov 子空间加速法相比, 拟议的方案需要更多的迭代法, 但执行和保留与未加速法基本相同的计算成本是微不足道的。 在固定循环矩阵仅以最小和最大的电子值为基础, 且仅以最小和最大的电子元值为基础, 且固定的循环矩阵只有真实的二次值, 得出固定的最佳参数的明确公式。 固定参数和相应的趋同系数显示, 当迭代矩阵也含有复杂的电子值, 并包含在复杂平面的硬盘中时, 将保持其最佳性。 根据最小和最大的真实电子值的相同信息, 与Chebyshev 的加速率( 底部限制信息 Chebyshev 加速度) 进行比较表明, Nesterov 的计算方法更加坚固, 因为它在更大的域域域上仍然最优化, 当迭代矩阵确实具有一些复杂的电子特性值时, 。 Numicalalalalalalalal 和3.1 estalestalgestalgest sal salizewgismal 。