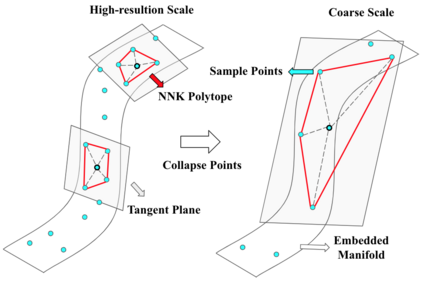
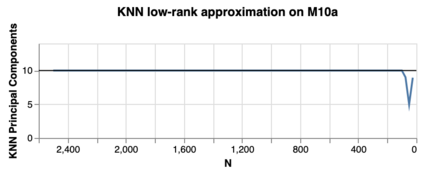
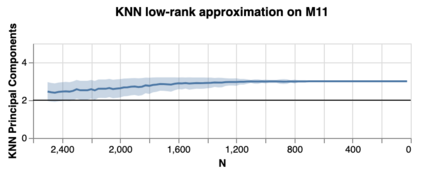
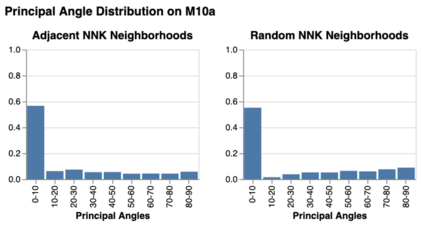
Modern machine learning systems are increasingly trained on large amounts of data embedded in high-dimensional spaces. Often this is done without analyzing the structure of the dataset. In this work, we propose a framework to study the geometric structure of the data. We make use of our recently introduced non-negative kernel (NNK) regression graphs to estimate the point density, intrinsic dimension, and the linearity of the data manifold (curvature). We further generalize the graph construction and geometric estimation to multiple scale by iteratively merging neighborhoods in the input data. Our experiments demonstrate the effectiveness of our proposed approach over other baselines in estimating the local geometry of the data manifolds on synthetic and real datasets.
翻译:现代机器学习系统越来越多地接受高维空间内嵌的大量数据培训。 通常在不分析数据集结构的情况下进行。 在这项工作中,我们提出了一个研究数据几何结构的框架。 我们利用我们最近推出的非负内核回归图来估计数据多重( 精度) 的点密度、 内在尺寸和线性( 精度) 。 我们进一步将图形构造和几何估计归纳为多重规模, 反复地将输入数据中的相邻区域合并 。 我们的实验表明, 在估计合成和真实数据集中数据元数的本地几何性方面, 我们所建议的方法比其他基线有效 。