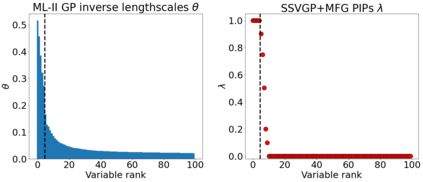
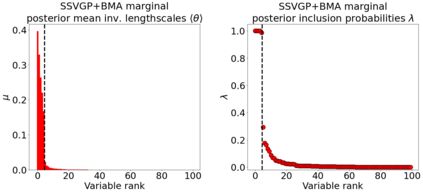
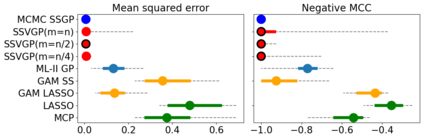
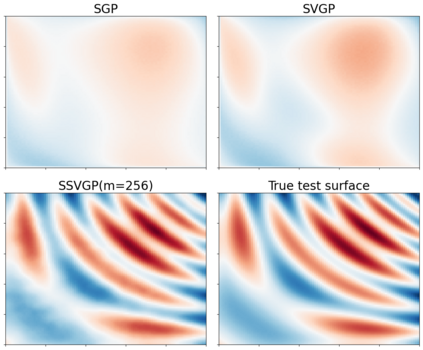
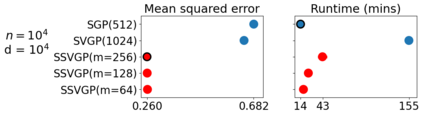
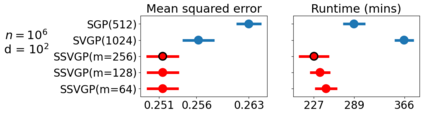
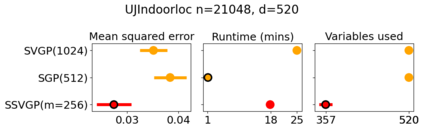
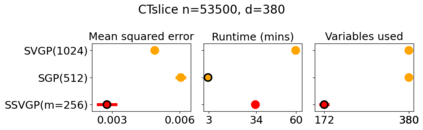
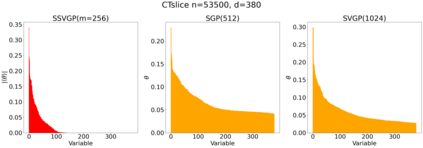
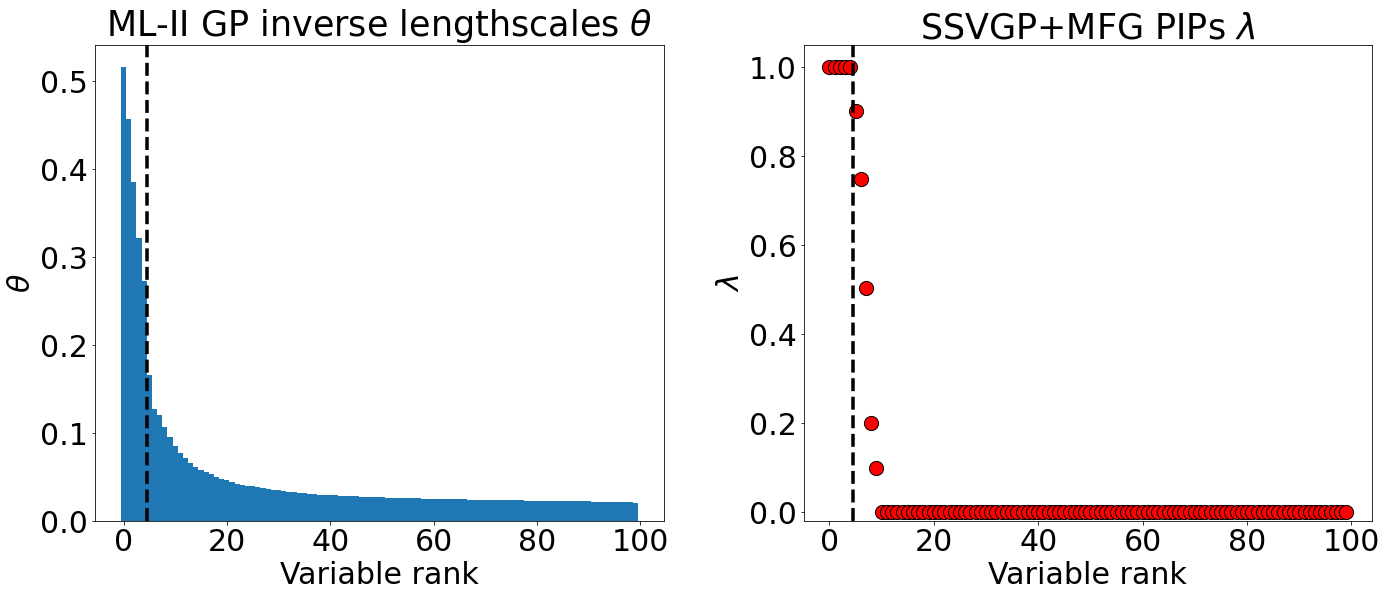
Variable selection in Gaussian processes (GPs) is typically undertaken by thresholding the inverse lengthscales of `automatic relevance determination' kernels, but in high-dimensional datasets this approach can be unreliable. A more probabilistically principled alternative is to use spike and slab priors and infer a posterior probability of variable inclusion. However, existing implementations in GPs are extremely costly to run in both high-dimensional and large-$n$ datasets, or are intractable for most kernels. As such, we develop a fast and scalable variational inference algorithm for the spike and slab GP that is tractable with arbitrary differentiable kernels. We improve our algorithm's ability to adapt to the sparsity of relevant variables by Bayesian model averaging over hyperparameters, and achieve substantial speed ups using zero temperature posterior restrictions, dropout pruning and nearest neighbour minibatching. In experiments our method consistently outperforms vanilla and sparse variational GPs whilst retaining similar runtimes (even when $n=10^6$) and performs competitively with a spike and slab GP using MCMC but runs up to $1000$ times faster.
翻译:Gausian 进程( GPs) 的变量选择通常采用“ 自动关联度确定” 内核的反长尺度, 而在高维数据集中, 这种方法可能是不可靠的。 更概率原则性的替代办法是使用钉钉和板的前缀, 并推出一个包含变量的外在概率。 但是, Gosian 中的现有实施对于在高维和大一美元数据集运行,或者对于大多数内核来说都是难处理的。 因此, 我们开发了一个快速和可扩缩的“ 自动关联度确定” 内核螺旋内核的变异性算法, 这个方法可以随任意的不同内核而可移动。 我们提高我们的算法能力, 以平均高于超光度光度计的方式适应Bayesian 模型的相关变量的宽度, 并且使用零温度后、 抛出和近邻的微型燃烧。 在实验中, 我们的方法始终优于 Vanilla 和 稀薄的变异性GPs, 同时保留类似的运行时间( 即使当 $M= 10) 和 快速运行到 和 10 MS 。