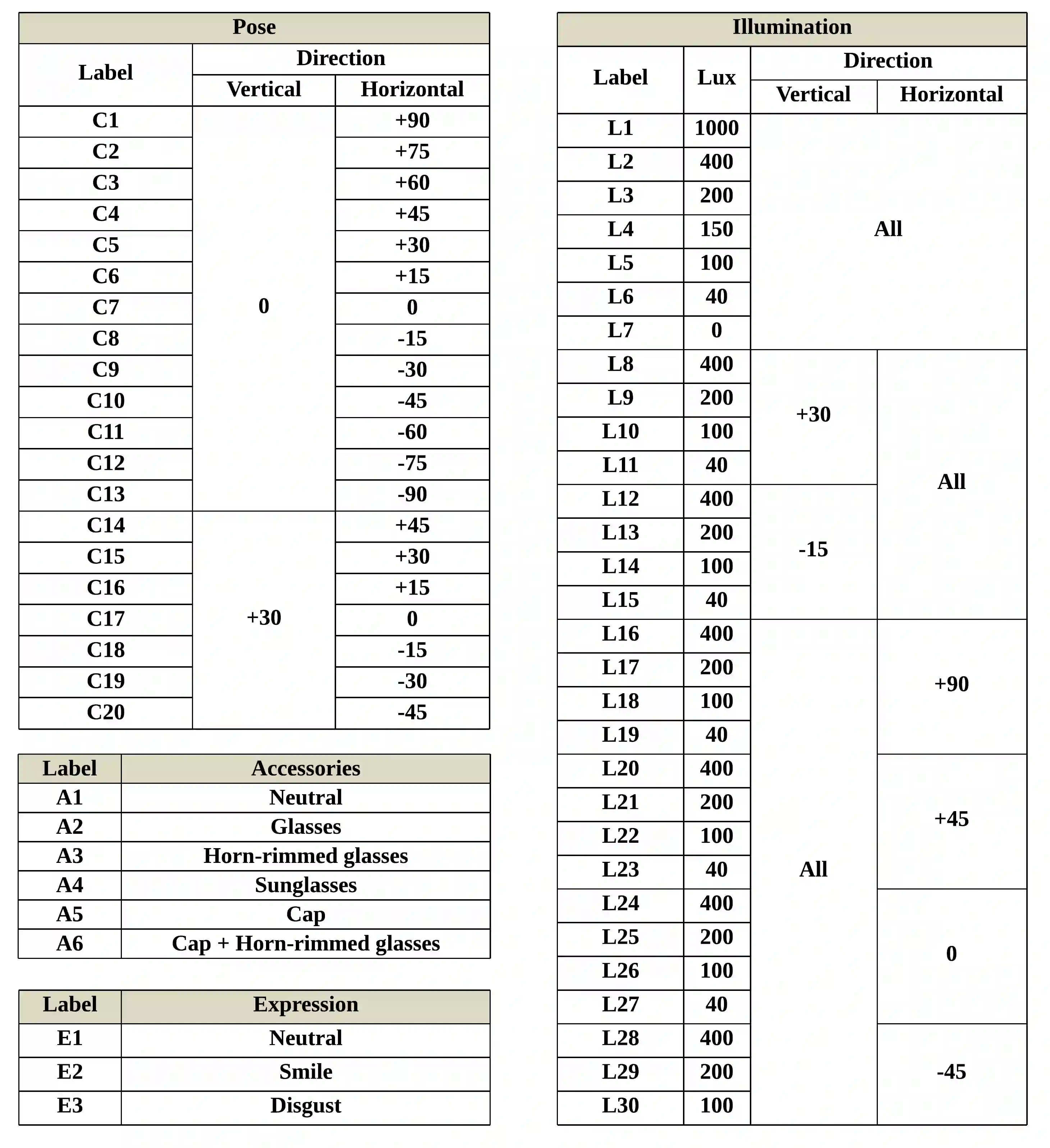
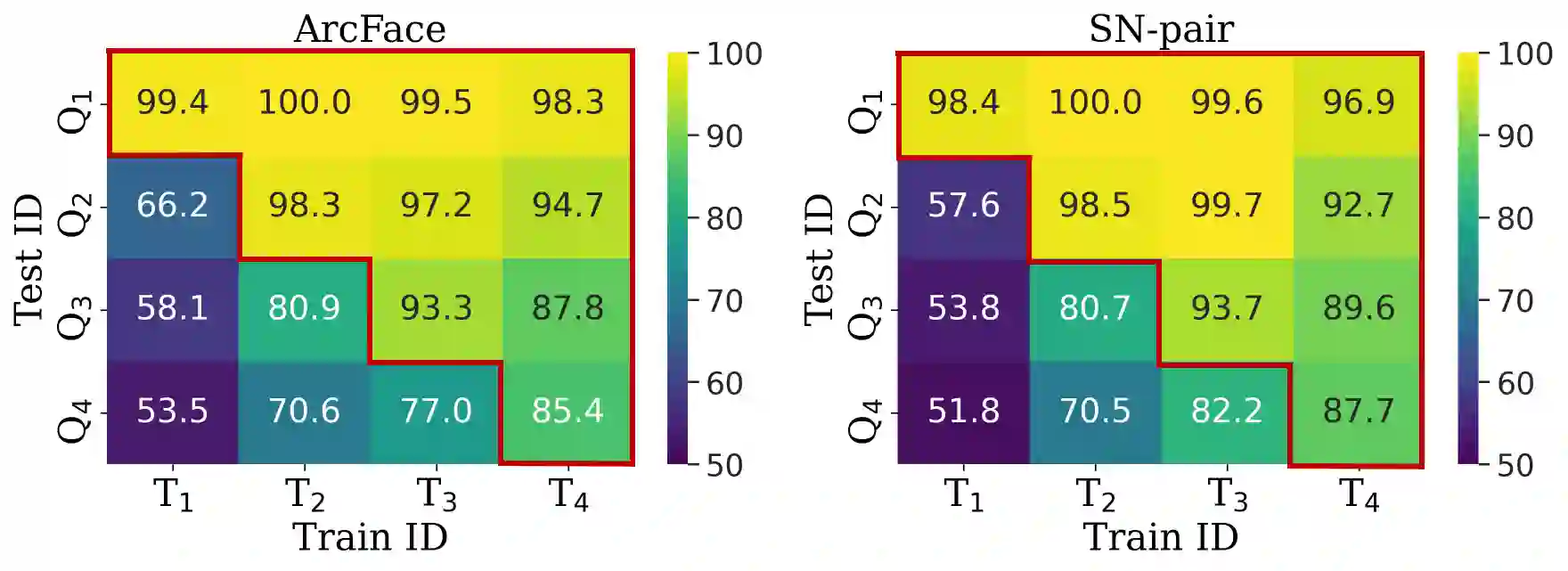
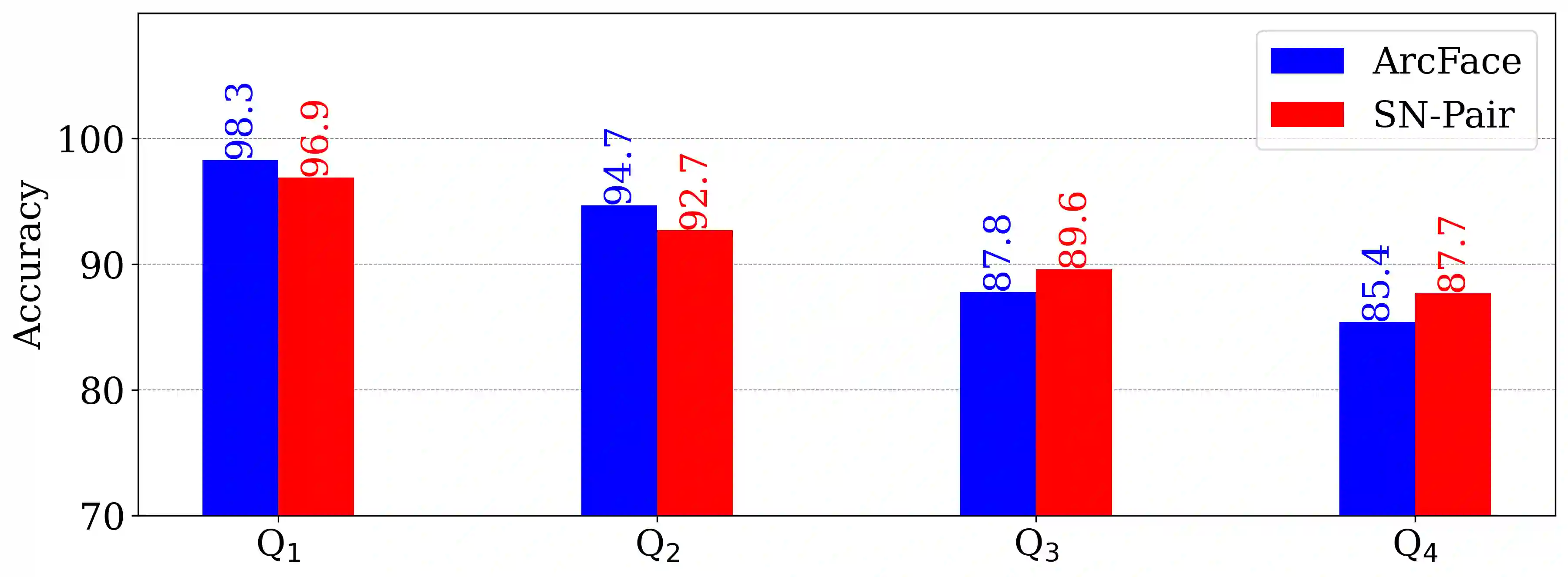
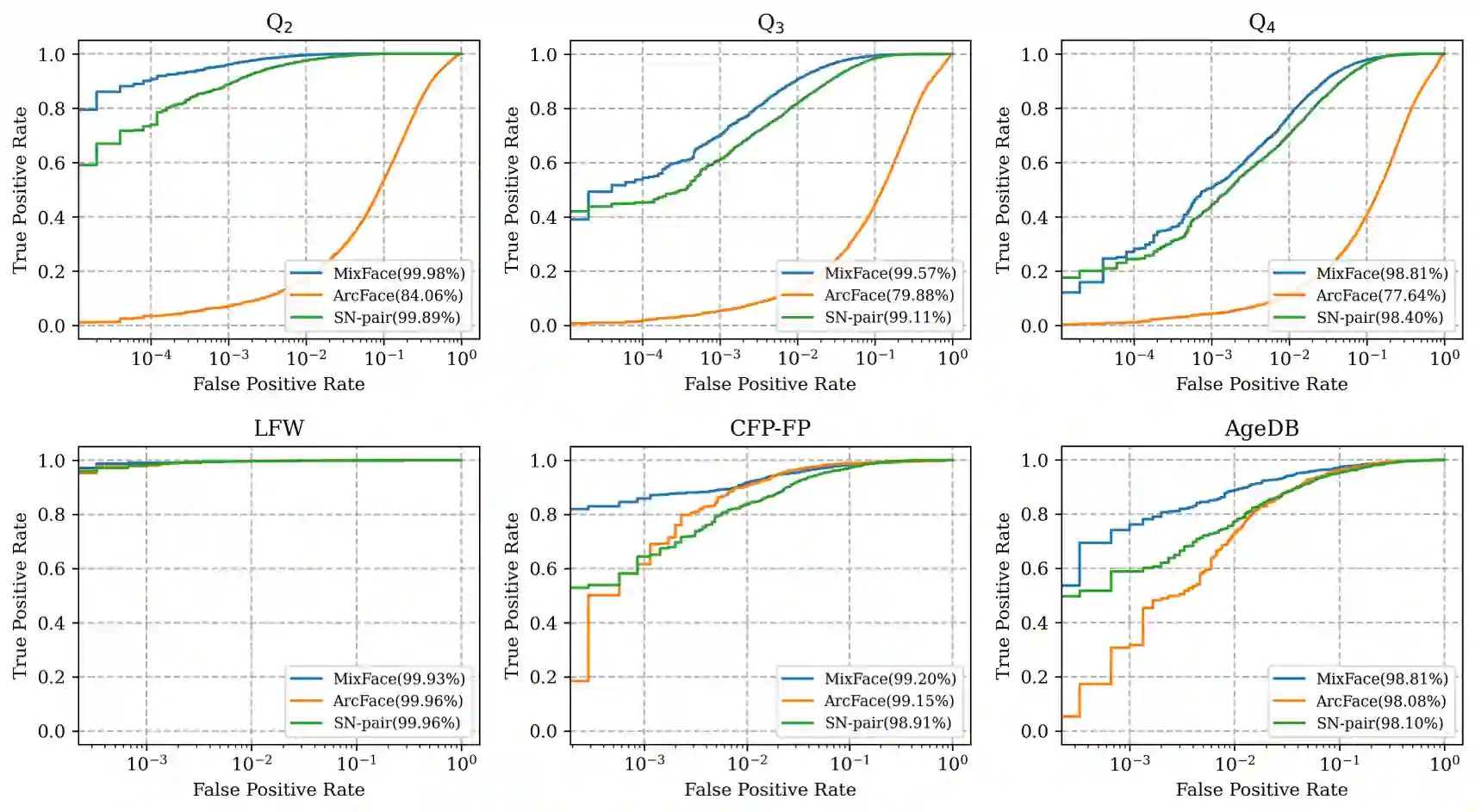
The performance of face recognition has become saturated for public benchmark datasets such as LFW, CFP-FP, and AgeDB, owing to the rapid advances in CNNs. However, the effects of faces with various fine-grained conditions on FR models have not been investigated because of the absence of such datasets. This paper analyzes their effects in terms of different conditions and loss functions using K-FACE, a recently introduced FR dataset with fine-grained conditions. We propose a novel loss function, MixFace, that combines classification and metric losses. The superiority of MixFace in terms of effectiveness and robustness is demonstrated experimentally on various benchmark datasets.
翻译:由于有线电视新闻网的快速发展,面部识别的性能已经饱和到诸如LFW、CFP-FP和AgeDB等公共基准数据集的状态,然而,由于缺乏这类数据集,没有调查面部与各种细微条件对FR模型的影响,本文分析其在不同条件和损失功能方面的影响,K-FACE是最近推出的具有细微条件的FR数据集。我们提出了新的损失功能MixFace,它结合分类和计量损失。MixFace在效力和稳健性方面的优越性在各种基准数据集上得到了实验性证明。