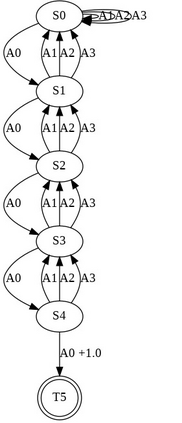
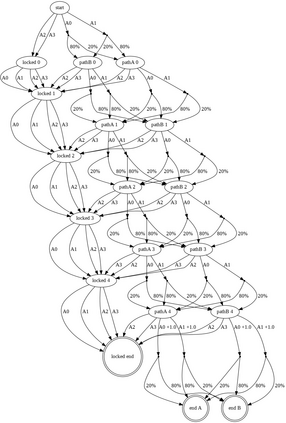
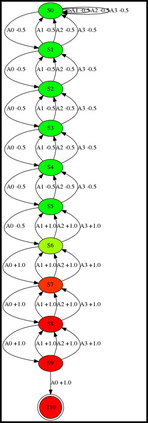
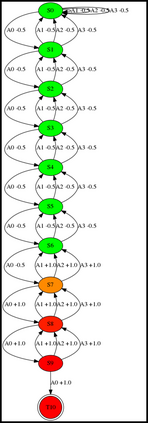
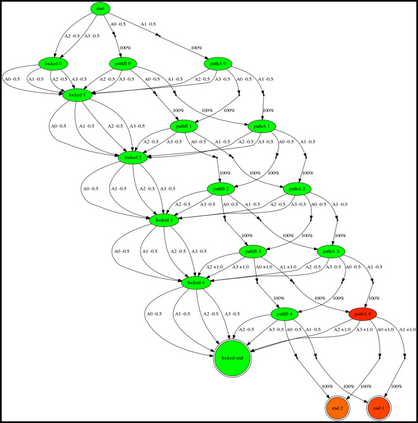
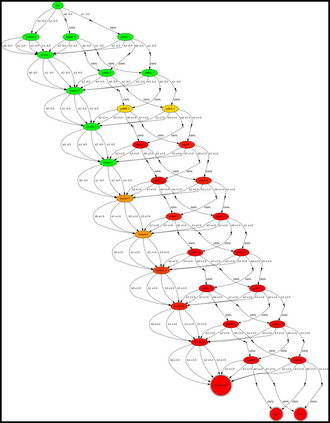
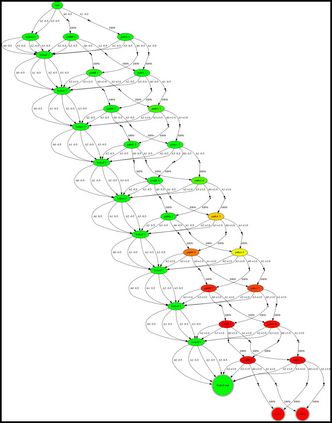
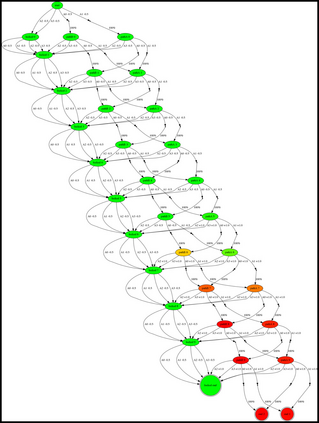
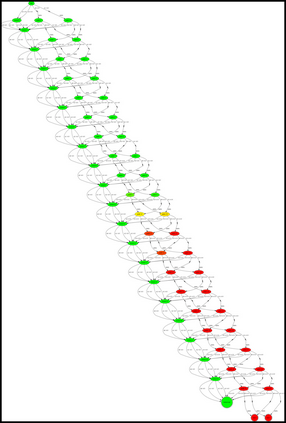
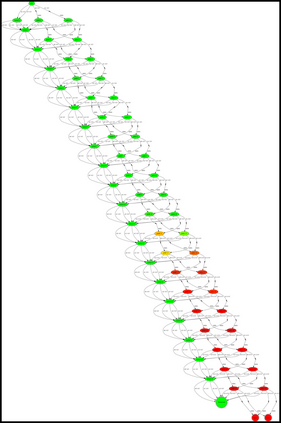
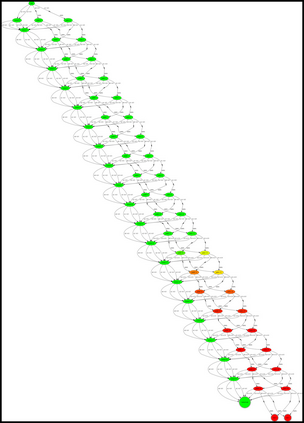
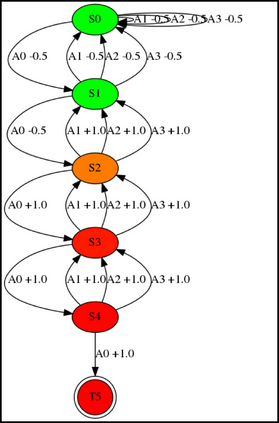
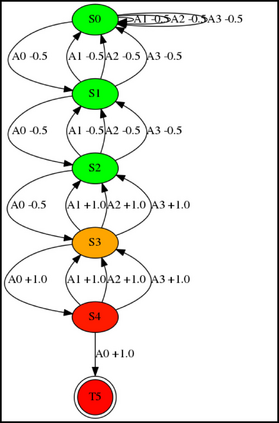
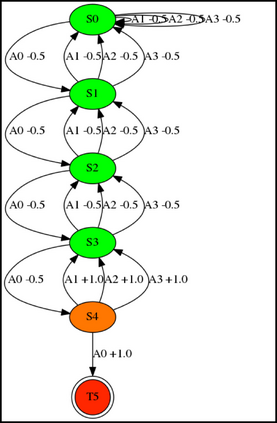
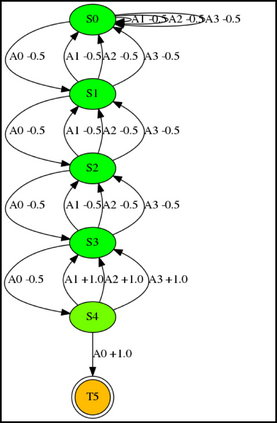
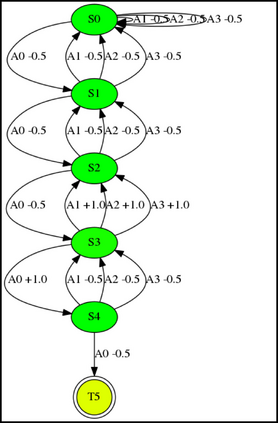
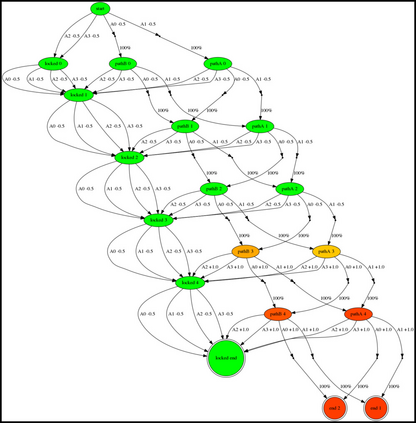
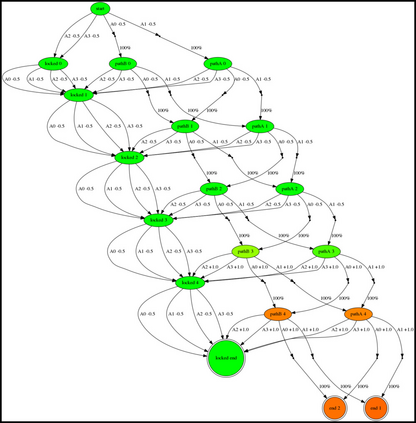
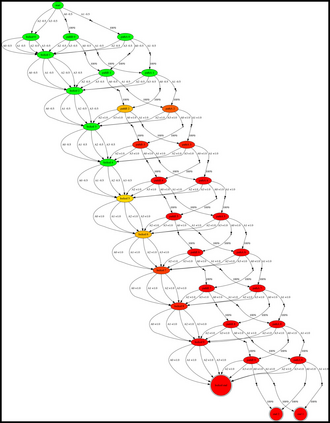
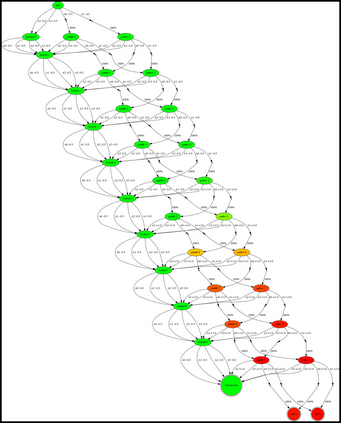
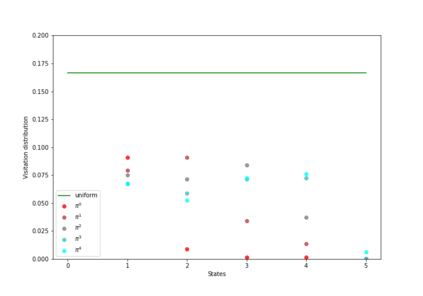
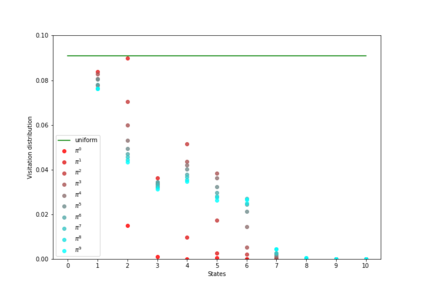
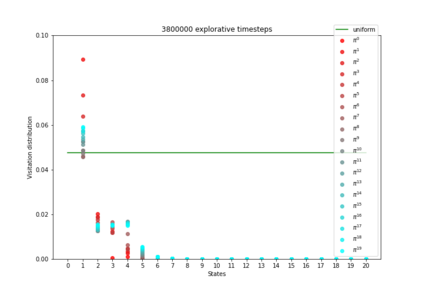
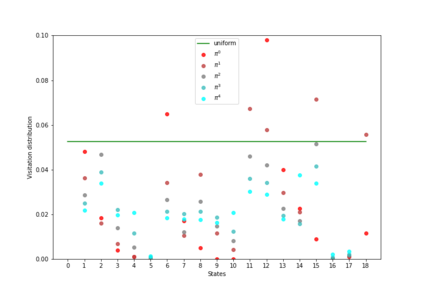
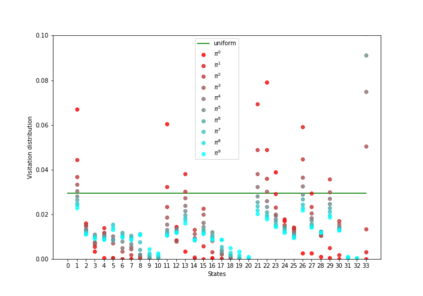
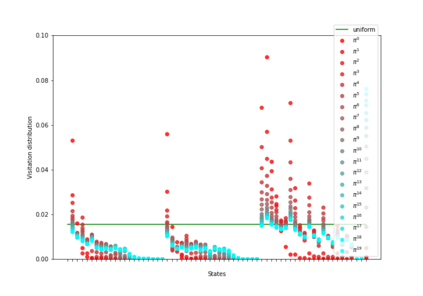
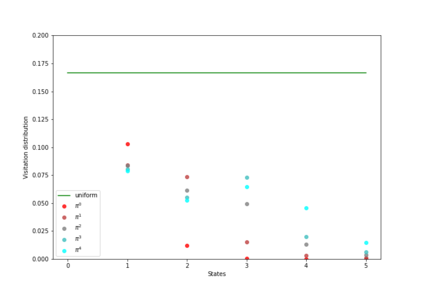
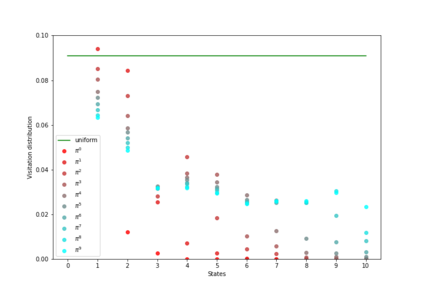
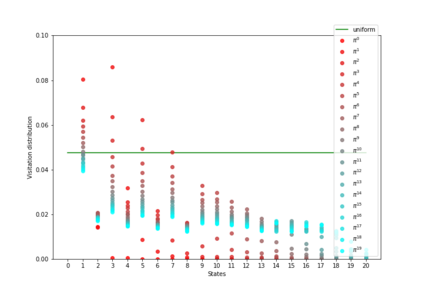
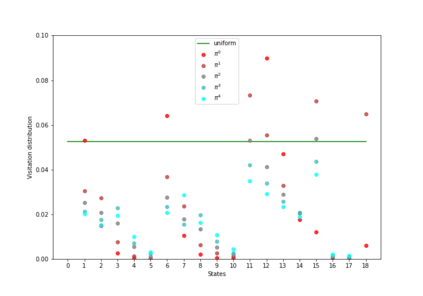
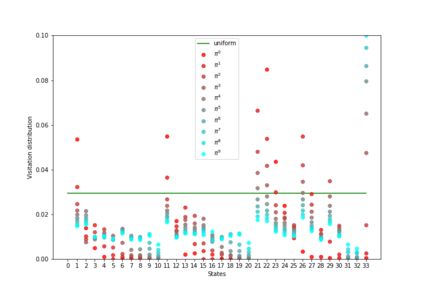
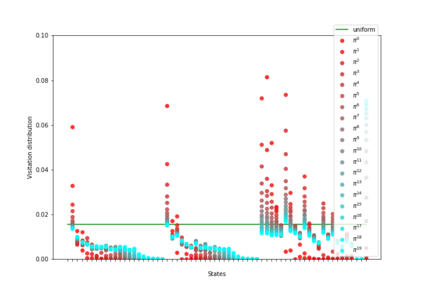
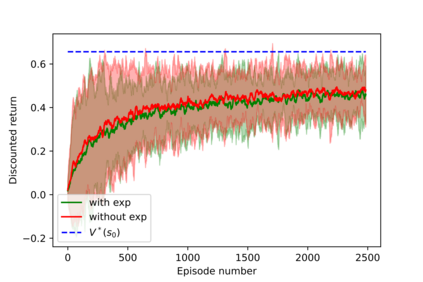
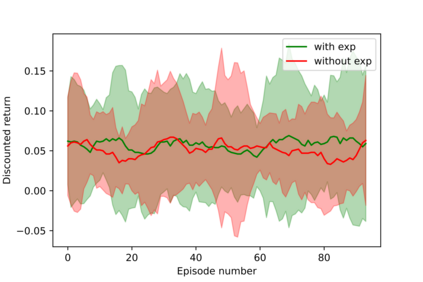
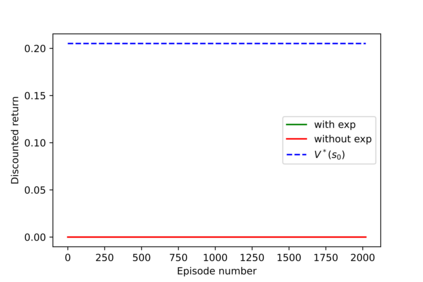
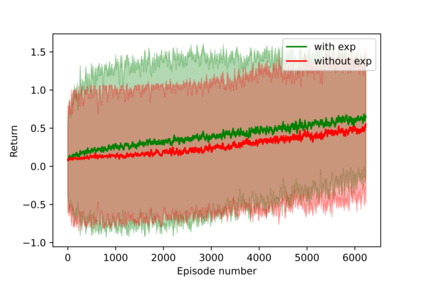
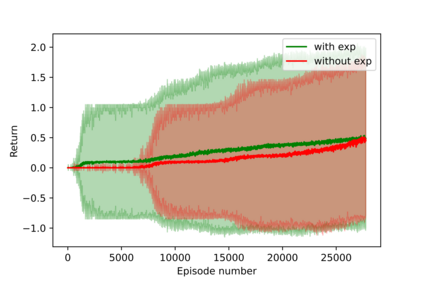
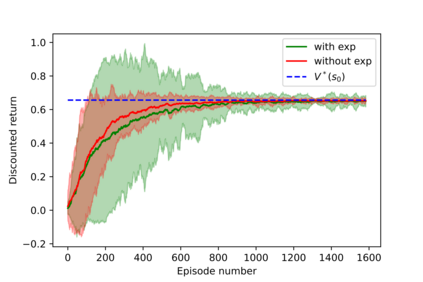
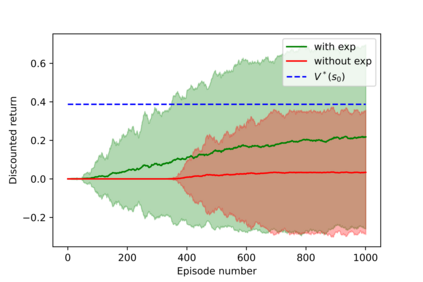
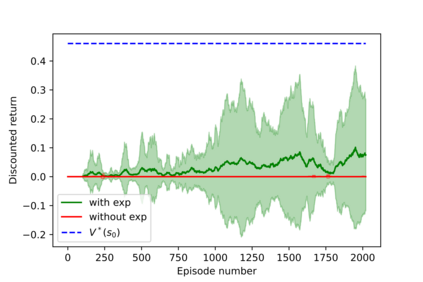
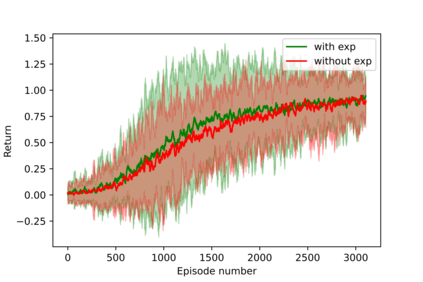
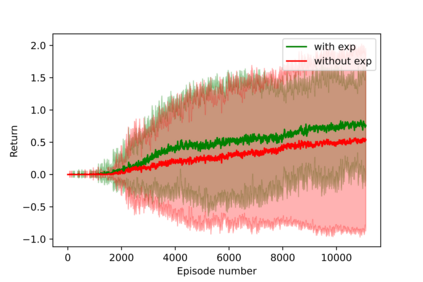
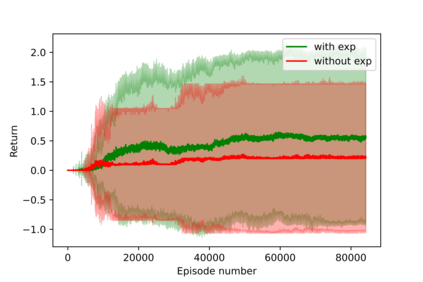
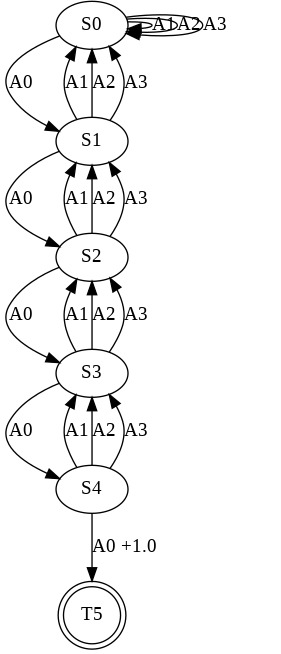
Having access to an exploring restart distribution (the so-called wide coverage assumption) is critical with policy gradient methods. This is due to the fact that, while the objective function is insensitive to updates in unlikely states, the agent may still need improvements in those states in order to reach a nearly optimal payoff. For this reason, wide coverage is used in some form when analyzing theoretical properties of practical policy gradient methods. However, this assumption can be unfeasible in certain environments, for instance when learning is online, or when restarts are possible only from a fixed initial state. In these cases, classical policy gradient algorithms can have very poor convergence properties and sample efficiency. In this paper, we develop Curious Explorer, a novel and simple iterative state space exploration strategy that can be used with any starting distribution $\rho$. Curious Explorer starts from $\rho$, then using intrinsic rewards assigned to the set of poorly visited states produces a sequence of policies, each one more exploratory than the previous one in an informed way, and finally outputs a restart model $\mu$ based on the state visitation distribution of the exploratory policies. Curious Explorer is provable, in the sense that we provide theoretical upper bounds on how often an optimal policy visits poorly visited states. These bounds can be used to prove PAC convergence and sample efficiency results when a PAC optimizer is plugged in Curious Explorer. This allows to achieve global convergence and sample efficiency results without any coverage assumption for REINFORCE, and potentially for any other policy gradient method ensuring PAC convergence with wide coverage. Finally, we plug (the output of) Curious Explorer into REINFORCE and TRPO, and show empirically that it can improve performance in MDPs with challenging exploration.
翻译:获取探索重新启动分布(所谓的广度覆盖假设)对于政策梯度方法至关重要。 这是因为, 虽然目标功能对不可行国家的最新信息不敏感, 但目标功能对于目标功能对于不可行国家的最新信息并不敏感, 但代理商仍然需要在这些国家中做出改进, 以便达到接近最佳的回报。 为此, 在分析实用政策梯度方法的理论属性时, 以某种形式使用宽度覆盖。 但是, 在某些环境中, 这种假设可能是行不通的, 比如当学习是在线的, 或者只有在固定的初始状态下才可能重新启动。 在这些情况下, 经典的政策梯度算可能具有非常差的趋同特性和样本效率。 在本文中, 我们开发了好奇的探索器, 一个新颖和简单的迭接的状态空间探索策略, 可以在开始分配时使用 $ror 。 好奇的探索器将产生一系列的政策序列, 每一次比前一次更深入的探索, 最终输出一个基于国家访问的重度模型 。 令人好奇的探索器探索器将最终显示我们如何在不精细的 ORC 访问时, 。