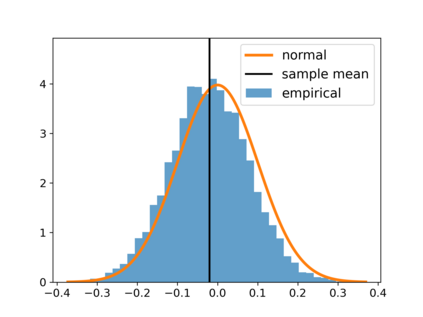
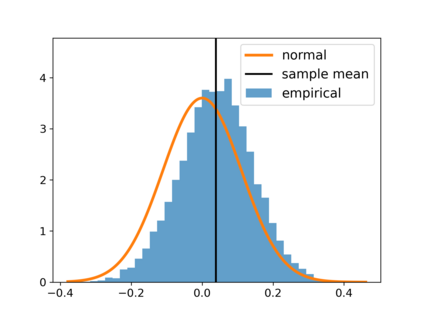
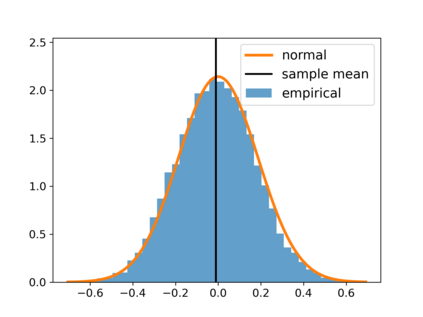
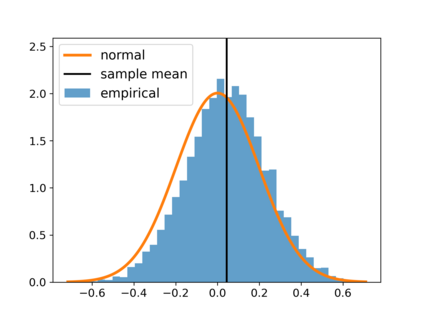
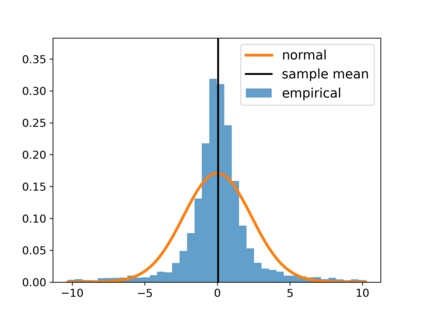
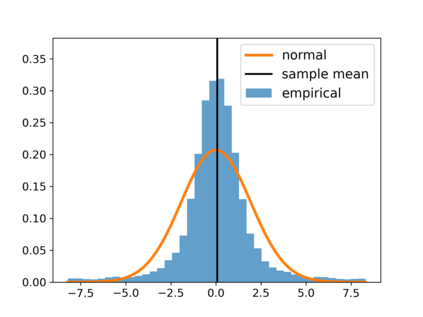
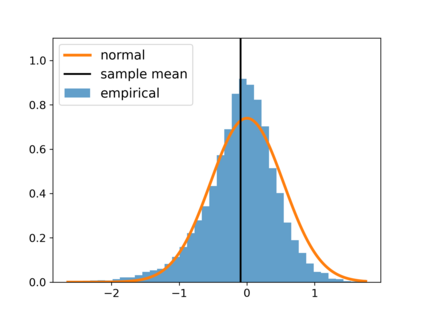
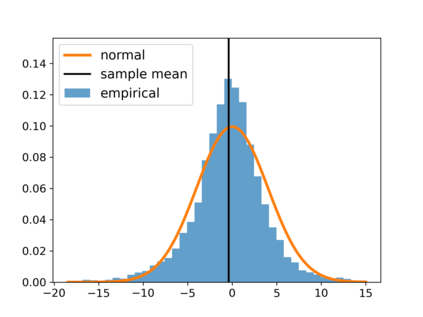
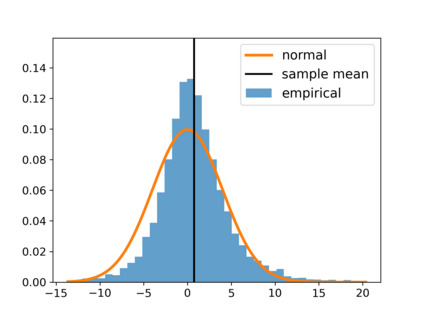
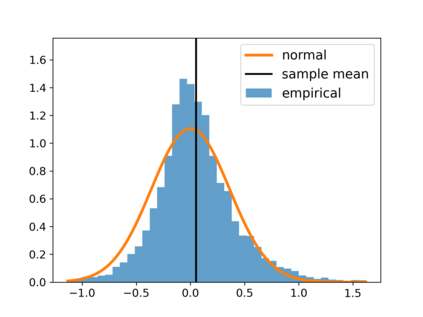
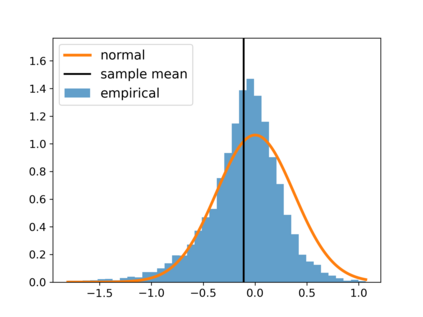
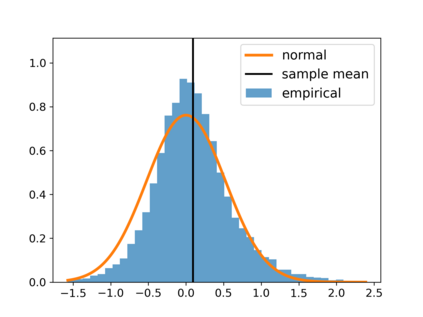
With the fast development of big data, it has been easier than before to learn the optimal decision rule by updating the decision rule recursively and making online decisions. We study the online statistical inference of model parameters in a contextual bandit framework of sequential decision-making. We propose a general framework for online and adaptive data collection environment that can update decision rules via weighted stochastic gradient descent. We allow different weighting schemes of the stochastic gradient and establish the asymptotic normality of the parameter estimator. Our proposed estimator significantly improves the asymptotic efficiency over the previous averaged SGD approach via inverse probability weights. We also conduct an optimality analysis on the weights in a linear regression setting. We provide a Bahadur representation of the proposed estimator and show that the remainder term in the Bahadur representation entails a slower convergence rate compared to classical SGD due to the adaptive data collection.
翻译:随着海量数据的快速发展,通过更新回溯性决定规则并作出在线决定来学习最佳决策规则比以往容易得多。我们研究了在相继决策的背景土匪框架中模型参数的在线统计推论。我们提出了在线和适应性数据收集环境的总体框架,该框架可以通过加权随机梯度梯度下降更新决策规则。我们允许随机梯度的不同加权办法,并建立了参数测深器的无症状常态。我们提议的测深器通过反概率权重,大大提高了先前的平均 SGD 方法的无症状效率。我们还对线性回归环境中的权重进行了最佳分析。我们提供了拟议估算器的巴哈杜尔语代表,并表明由于适应性数据收集,巴哈杜尔语代表的剩余任期与古典 SGD 的融合速度要慢。