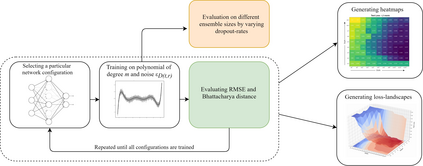
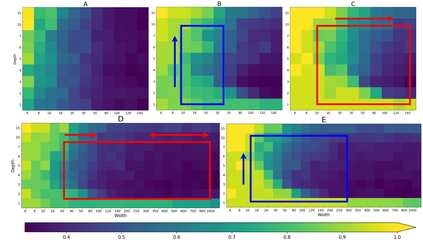
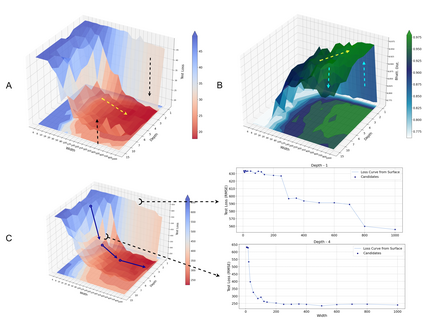
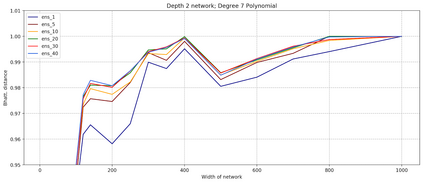
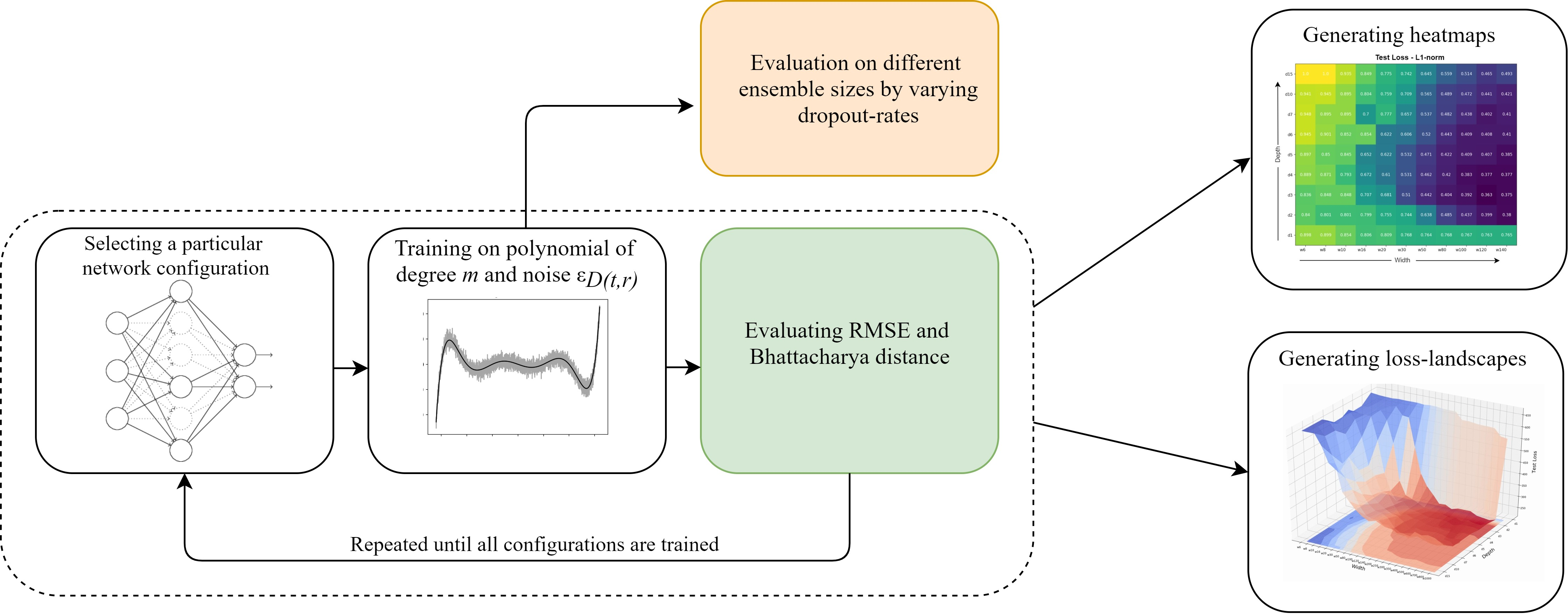
Advances in neural architecture search, as well as explainability and interpretability of connectionist architectures, have been reported in the recent literature. However, our understanding of how to design Bayesian Deep Learning (BDL) hyperparameters, specifically, the depth, width and ensemble size, for robust function mapping with uncertainty quantification, is still emerging. This paper attempts to further our understanding by mapping Bayesian connectionist representations to polynomials of different orders with varying noise types and ratios. We examine the noise-contaminated polynomials to search for the combination of hyperparameters that can extract the underlying polynomial signals while quantifying uncertainties based on the noise attributes. Specifically, we attempt to study the question that an appropriate neural architecture and ensemble configuration can be found to detect a signal of any n-th order polynomial contaminated with noise having different distributions and signal-to-noise (SNR) ratios and varying noise attributes. Our results suggest the possible existence of an optimal network depth as well as an optimal number of ensembles for prediction skills and uncertainty quantification, respectively. However, optimality is not discernible for width, even though the performance gain reduces with increasing width at high values of width. Our experiments and insights can be directional to understand theoretical properties of BDL representations and to design practical solutions.
翻译:在最近的文献中报告了神经结构搜索的进展,以及连接建筑的可解释性和可解释性。然而,我们对于如何设计贝耶斯深海学习(BDL)超参数的理解,特别是深度、宽度和共合体大小,以便以不确定性量化的方式进行稳健的功能绘图,目前仍在出现。本文件试图通过绘制贝耶斯联系学家的表示图,加深我们对不同次序、不同噪音类型和比率的不同多音谱多音系的多音系的了解。我们研究了受噪音污染的多音系多音系,以寻找能够提取基本多音信号的超分光度计组合,同时根据噪音属性量化不确定性。具体地说,我们试图研究这样一个问题,即如何找到适当的神经结构和共和共通体大小,以便发现任何受不同分布分布和信号到噪声比例不同噪音污染的n-n-nomial(SNR)多音系的信号的信号信号。我们的结果显示,可能存在最佳网络深度,以及预测技能和不确定性量化解决方案的最佳数目。我们试图研究一个高度的深度,但最接近于深度的深度,我们更接近于深度的深度和深度的深度的深度,我们无法理解。