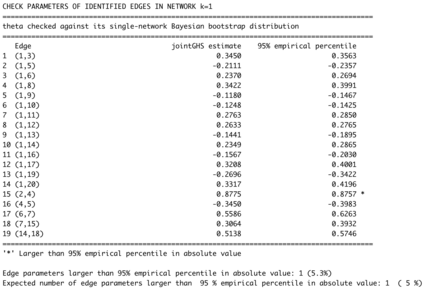
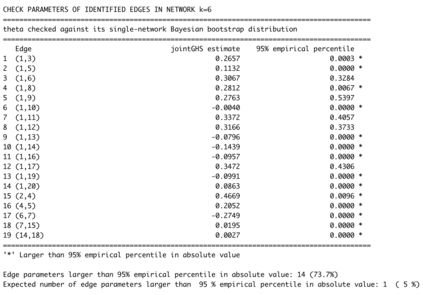
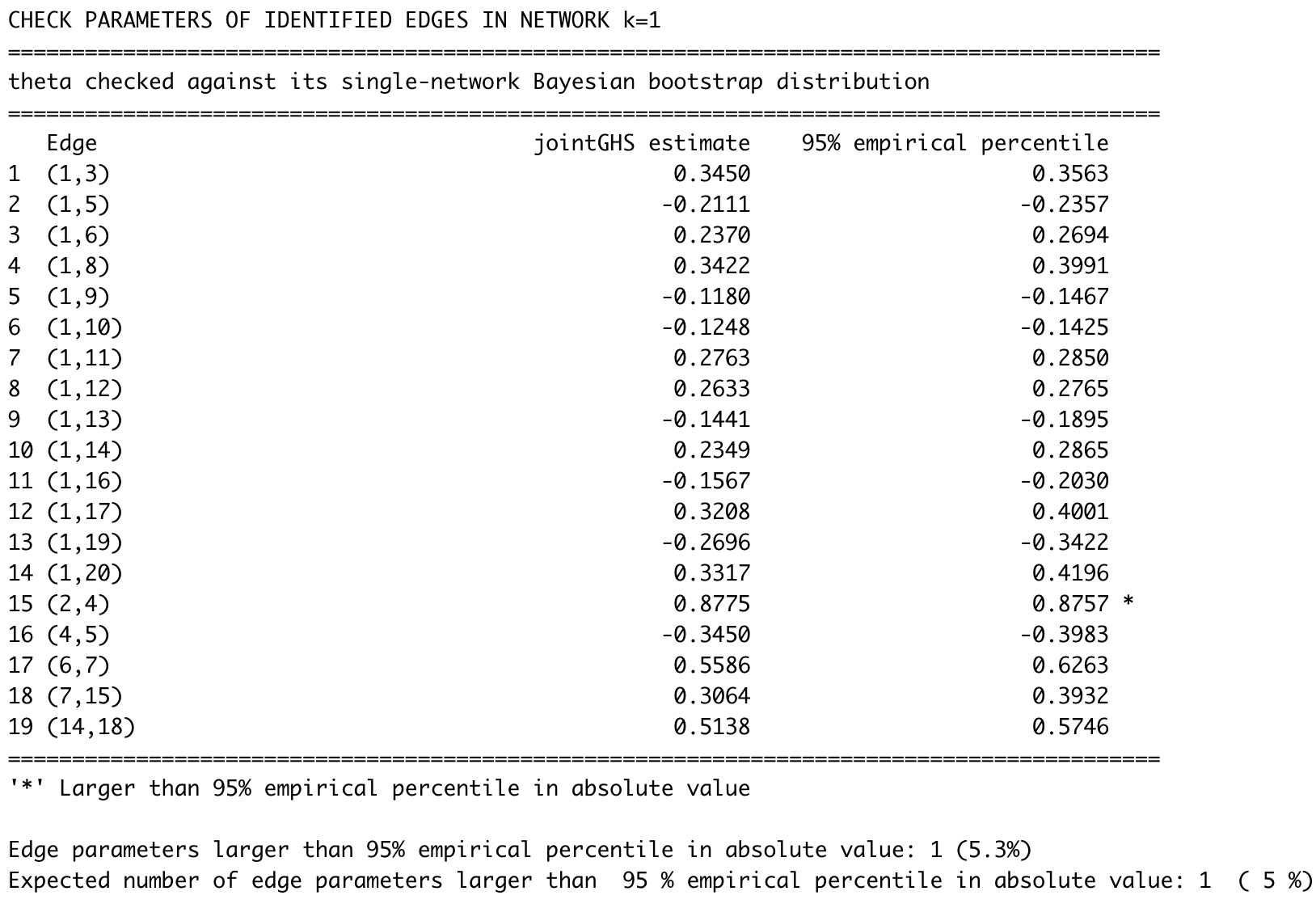
Network models are useful tools for modelling complex associations. If a Gaussian graphical model is assumed, conditional independence is determined by the non-zero entries of the inverse covariance (precision) matrix of the data. The Bayesian graphical horseshoe estimator provides a robust and flexible framework for precision matrix inference, as it introduces local, edge-specific parameters which prevent over-shrinkage of non-zero off-diagonal elements. However, for many applications such as statistical omics, the current implementation based on Gibbs sampling becomes computationally inefficient or even unfeasible in high dimensions. Moreover, the graphical horseshoe has only been formulated for a single network, whereas interest has grown in the network analysis of multiple data sets that might share common structures. We propose (i) a scalable expectation conditional maximisation (ECM) algorithm for obtaining the posterior mode of the precision matrix in the graphical horseshoe, and (ii) a novel joint graphical horseshoe estimator, which borrows information across multiple related networks to improve estimation. We show, on both simulated and real omics data, that our single-network ECM approach is more scalable than the existing graphical horseshoe Gibbs implementation, while achieving the same level of accuracy. We also show that our joint-network proposal successfully leverages shared edge-specific information between networks while still retaining differences, outperforming state-of-the-art methods at any level of network similarity.
翻译:网络模型是建模复杂协会的有用工具。 如果假设高斯图形模型是模拟复杂协会的有用工具。 如果假设高斯图形模型, 有条件的独立由数据逆差(精度)矩阵的非零条目决定。 Bayesian 图形马铃薯测量仪为精确矩阵推断提供了一个强有力和灵活的框架, 因为它引入了本地的、 边缘特定的参数, 防止非零离对角元素的过度缩小。 但是, 对于许多应用程序, 如统计缩影等, 以 Gibs 取样为基础的当前实施在计算上效率低下, 甚至高维度上是不可能做到的。 此外, 图形马蹄图只为单一的网络设计了非零分数( 精度 精度 ), 而对多个可能共享共同结构的数据集的网络分析也越来越感兴趣 。 我们建议 (i) (i) 为获取图形马座中非零离子的精度矩阵的外观模式, 以及 (ii) 新的联合图形马座估测器, 利用多个相关网络的信息来改进估算。 我们还在模拟和真实的网络上显示, 共同的精度方法上显示, 我们的深度网络的精度数据也显示, 我们的单个的精度水平上, 。