A survey of Bayesian Network structure learning

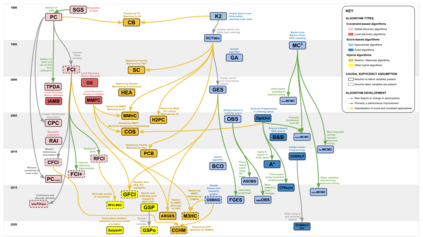
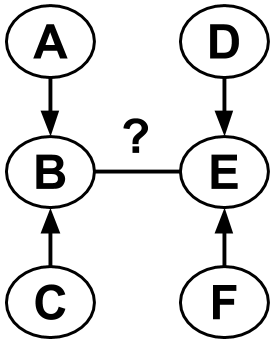
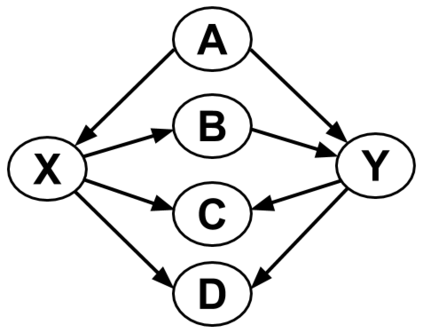
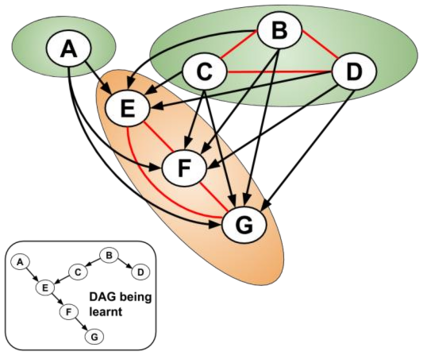
Bayesian Networks (BNs) have become increasingly popular over the last few decades as a tool for reasoning under uncertainty in fields as diverse as medicine, biology, epidemiology, economics and the social sciences. This is especially true in real-world areas where we seek to answer complex questions based on hypothetical evidence to determine actions for intervention. However, determining the graphical structure of a BN remains a major challenge, especially when modelling a problem under causal assumptions. Solutions to this problem include the automated discovery of BN graphs from data, constructing them based on expert knowledge, or a combination of the two. This paper provides a comprehensive review of combinatoric algorithms proposed for learning BN structure from data, describing 61 algorithms including prototypical, well-established and state-of-the-art approaches. The basic approach of each algorithm is described in consistent terms, and the similarities and differences between them highlighted. Methods of evaluating algorithms and their comparative performance are discussed including the consistency of claims made in the literature. Approaches for dealing with data noise in real-world datasets and incorporating expert knowledge into the learning process are also covered.