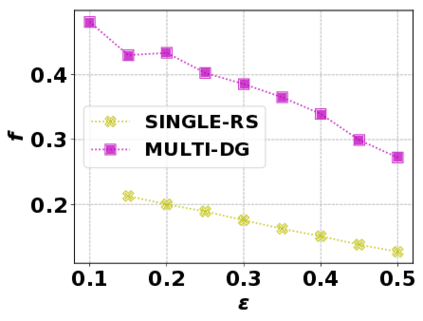
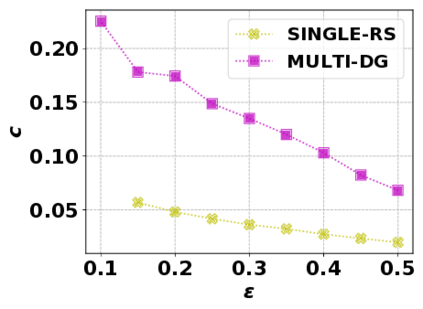
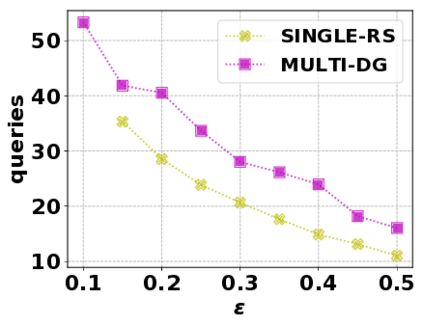
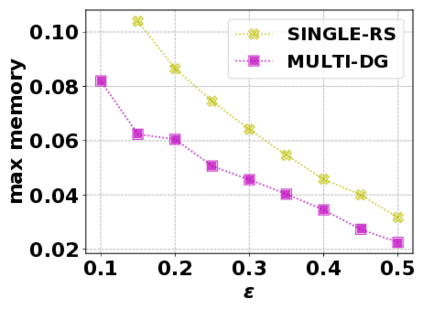
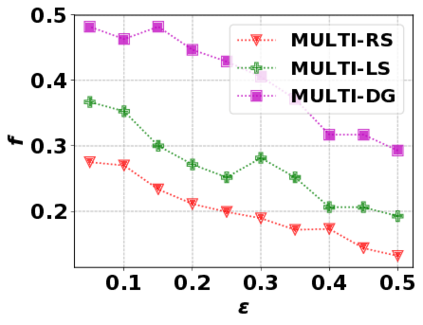
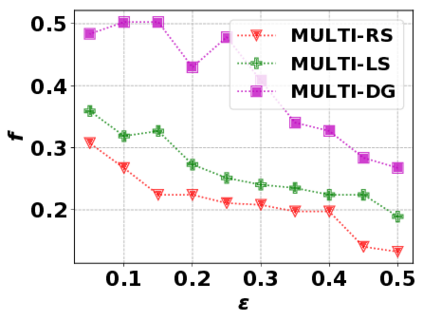
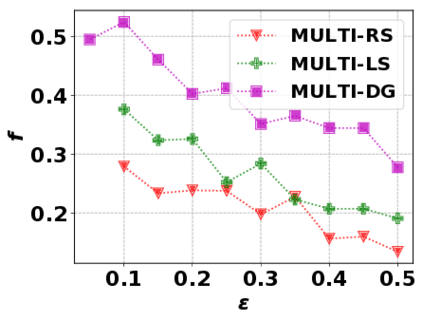
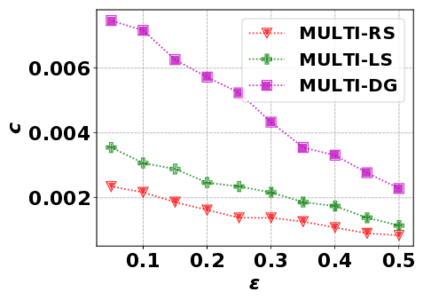
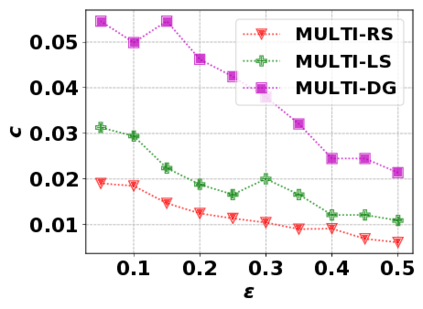
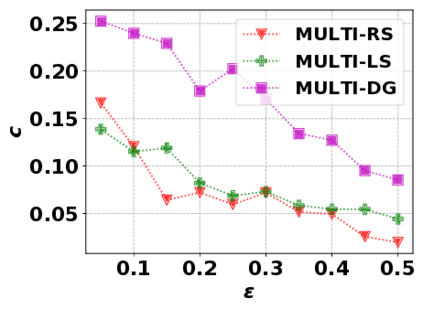
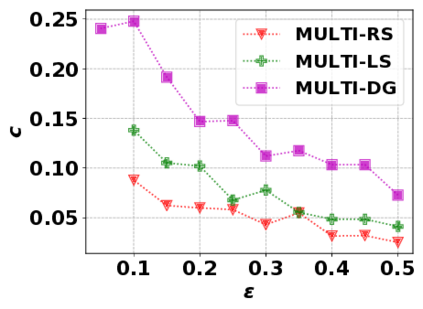
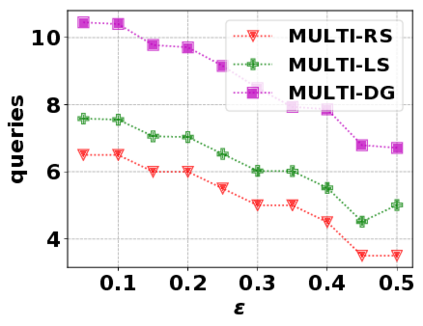
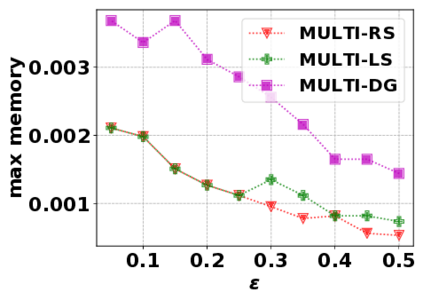
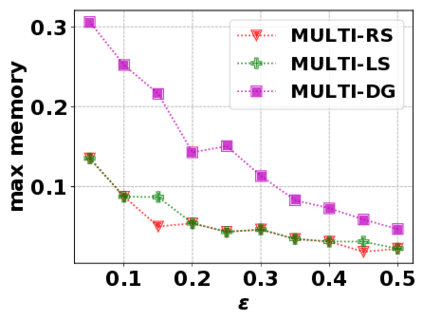
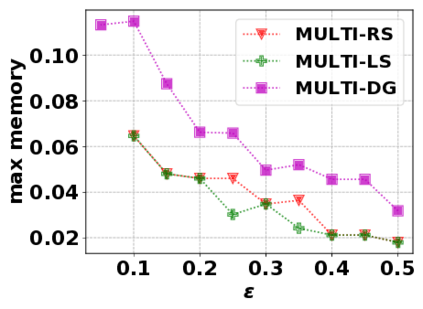
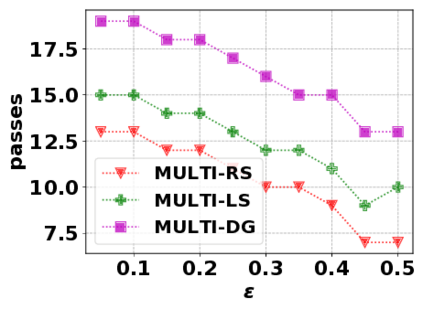
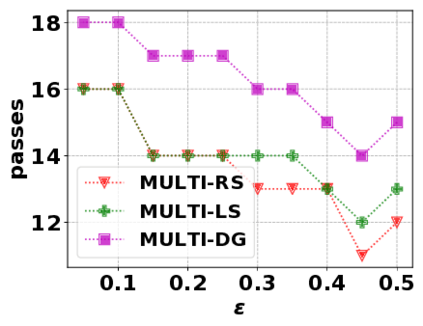
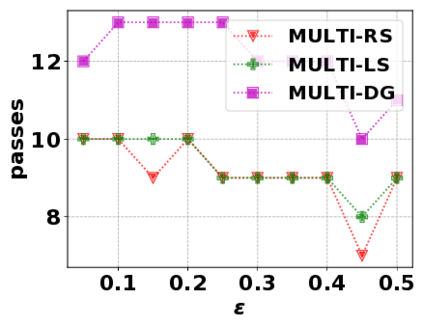
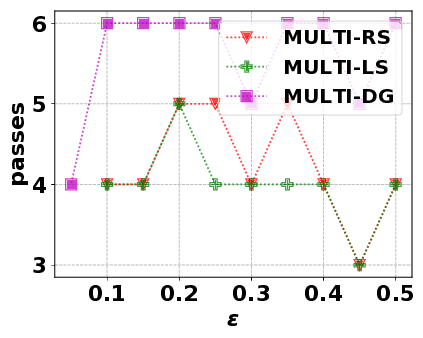
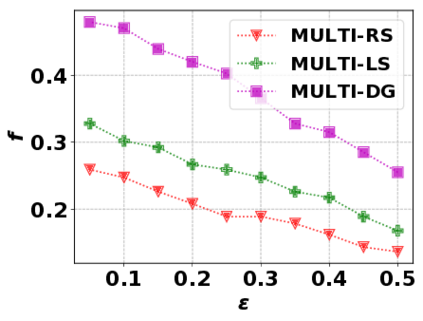
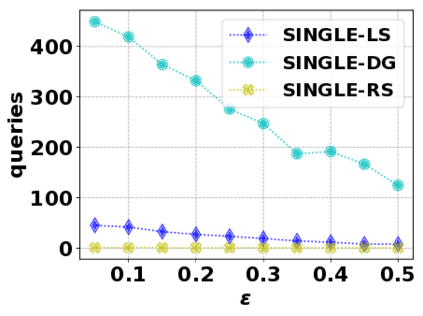
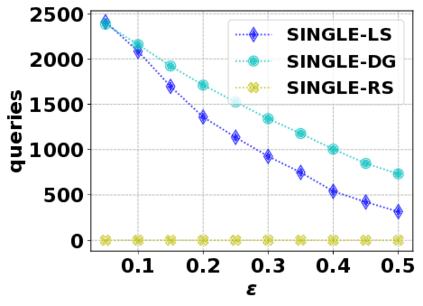
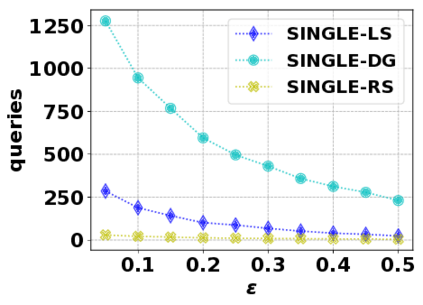
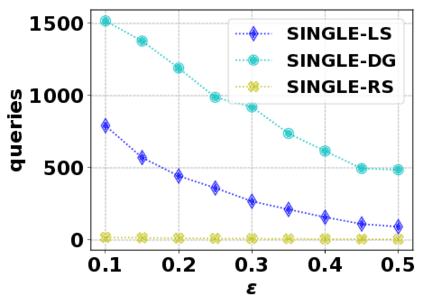
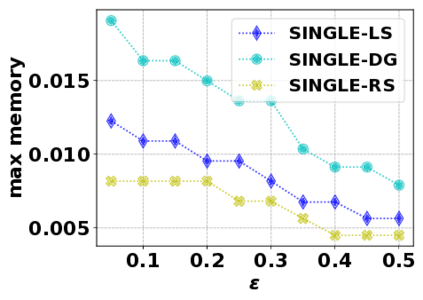
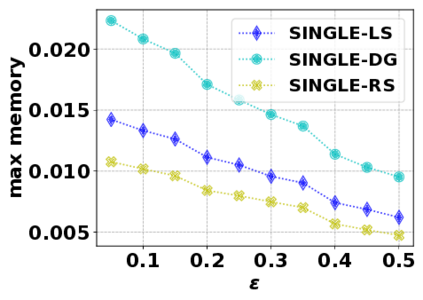
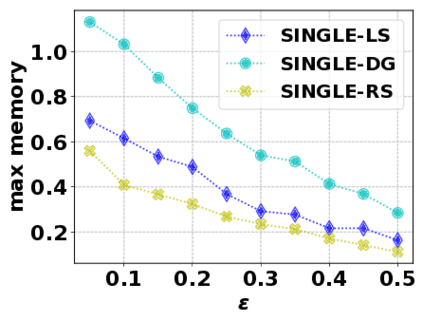
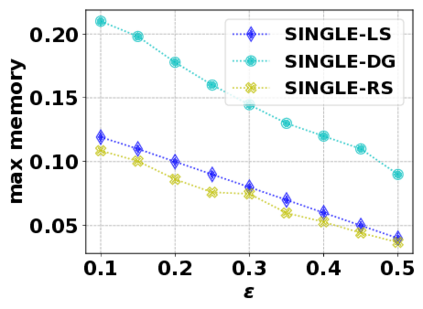
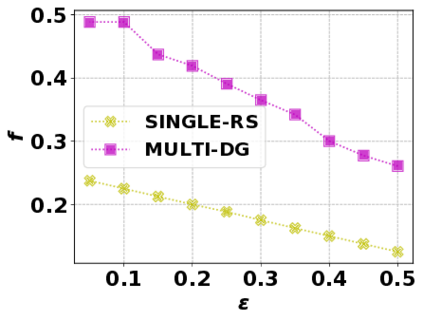
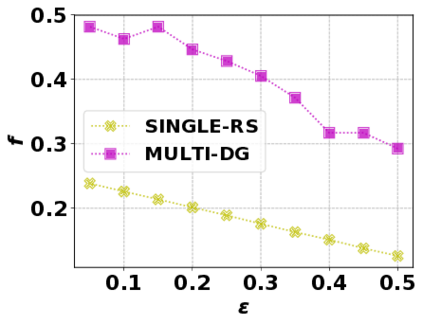
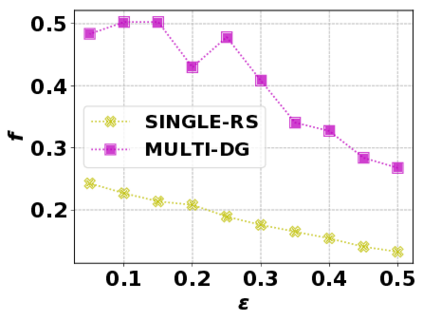
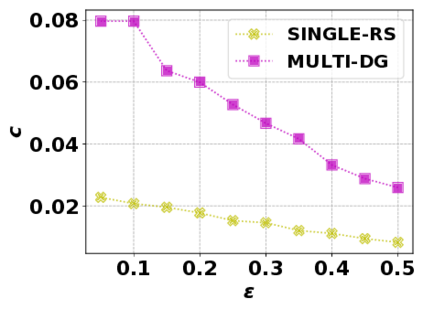
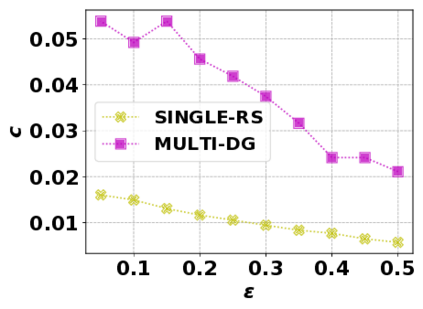
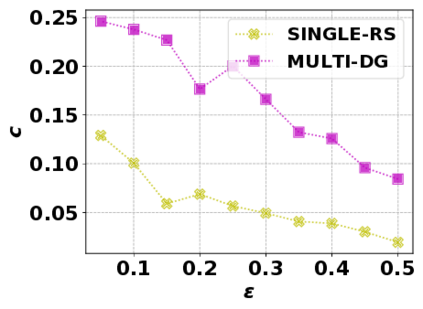
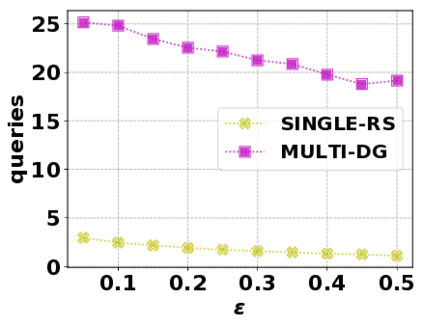
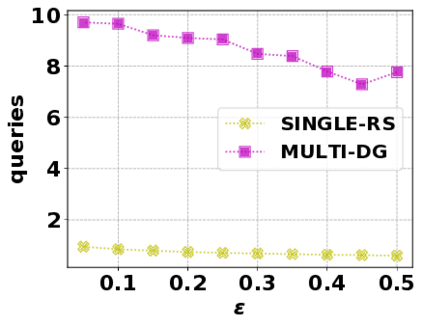
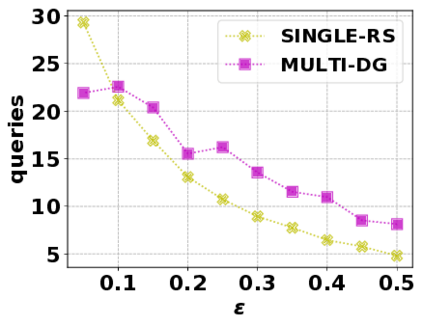
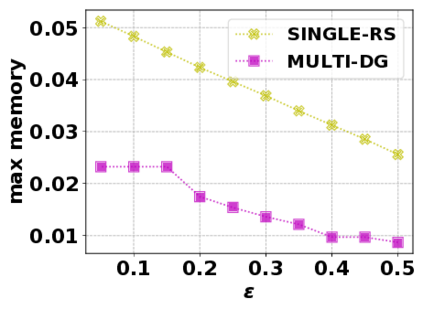
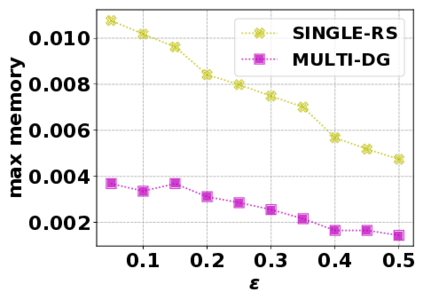
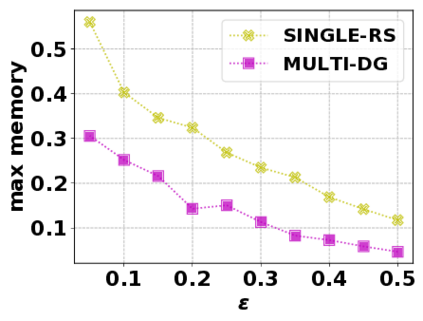
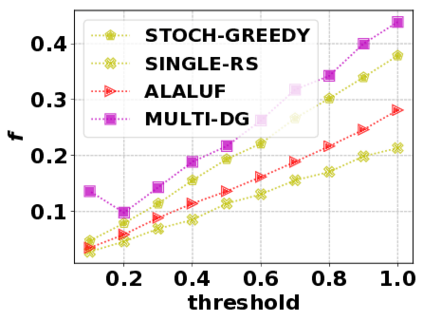
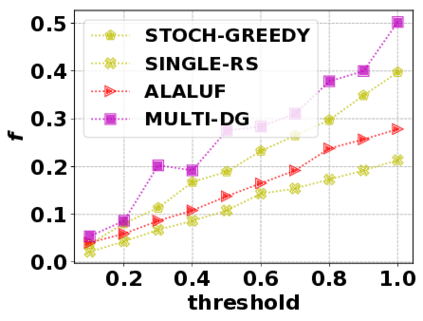
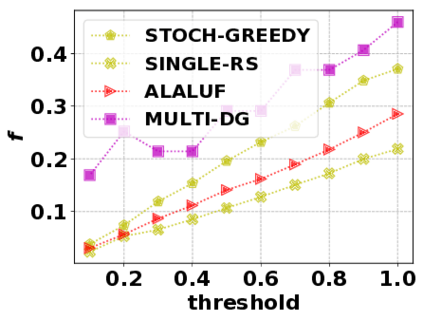
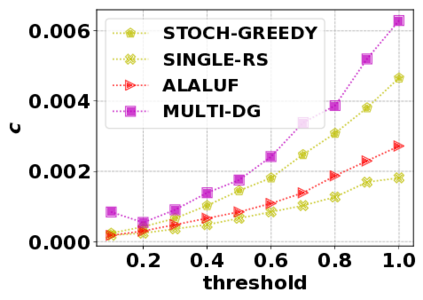
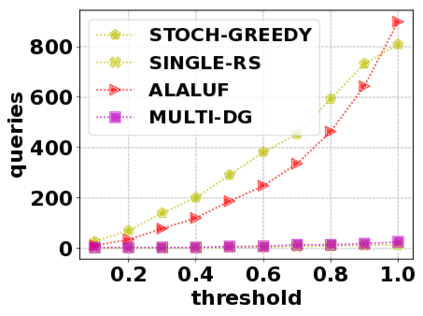
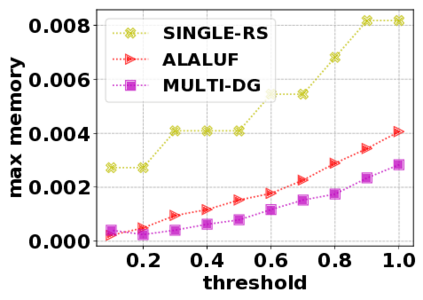
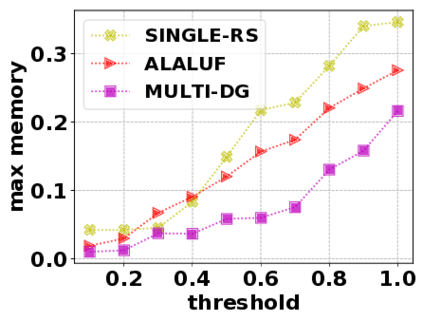
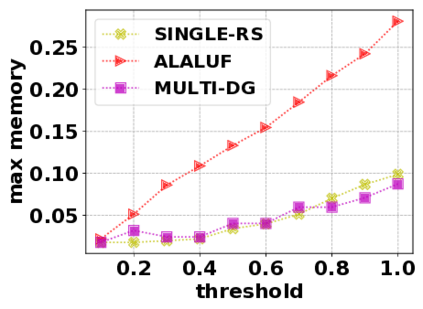
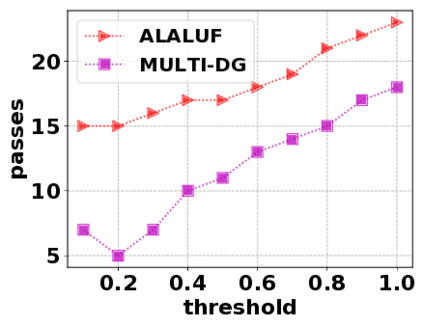
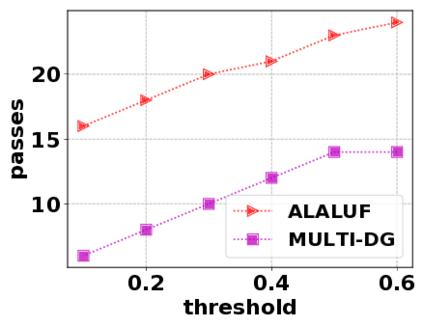
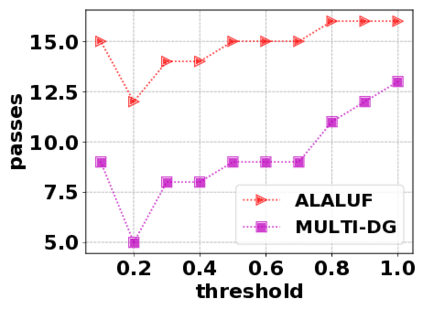
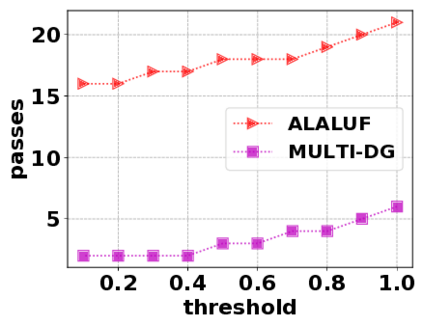
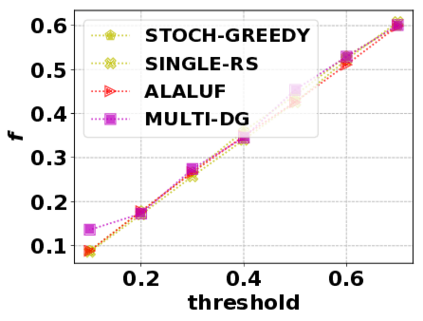
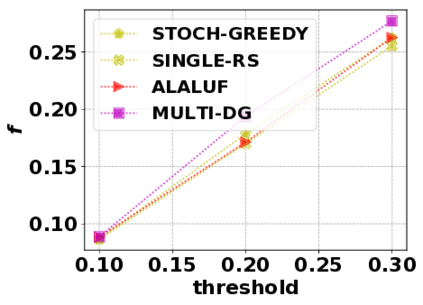
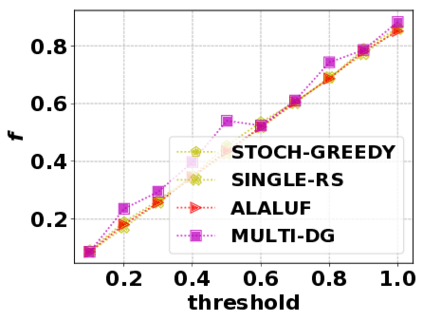
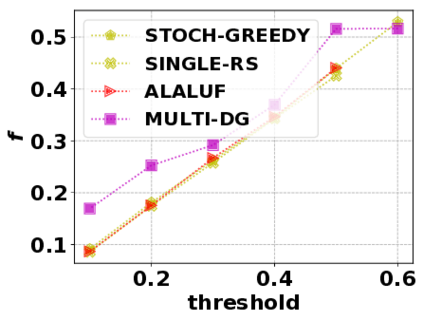
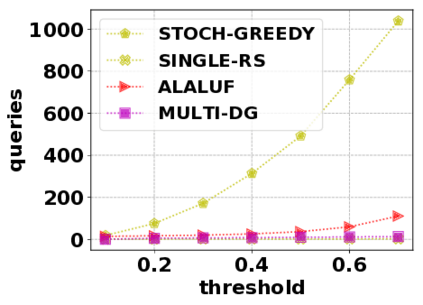
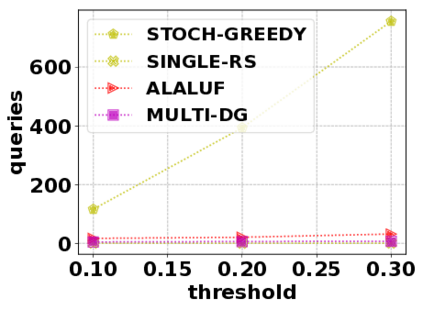
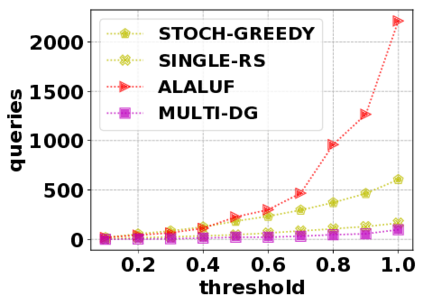
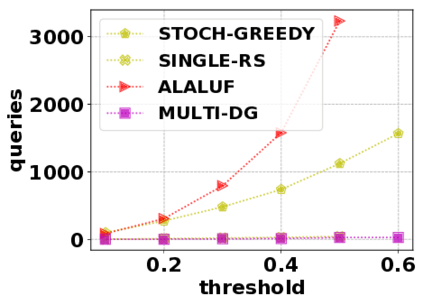
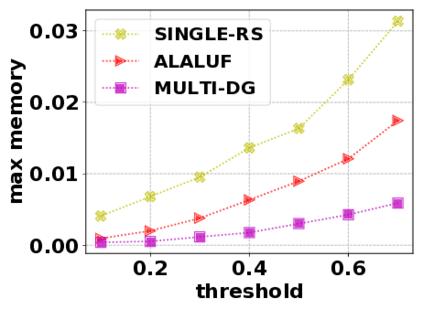
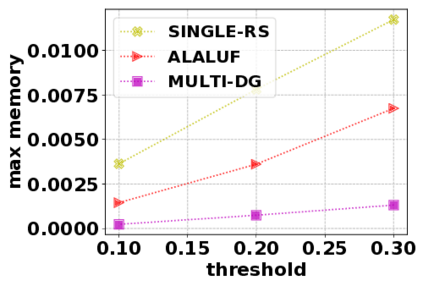
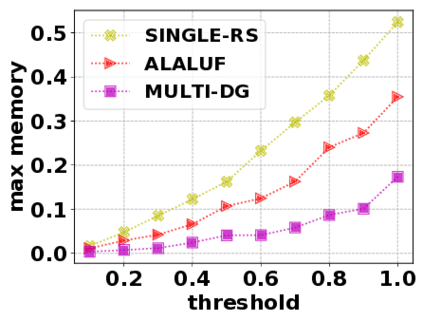
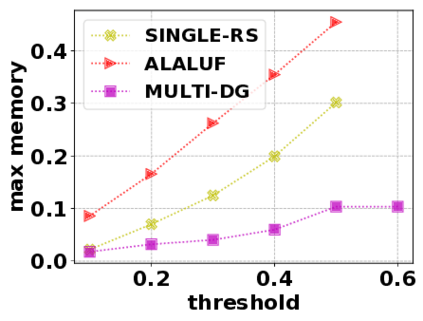
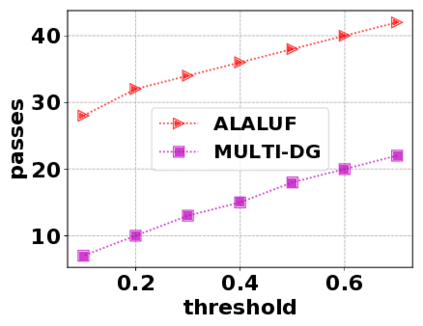
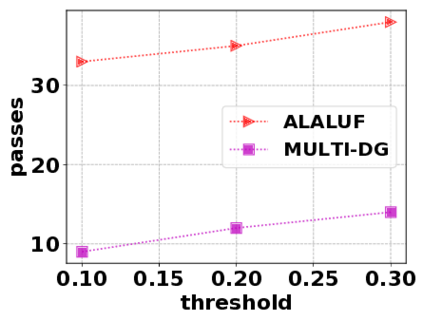
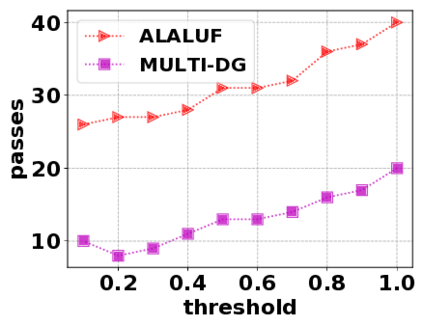
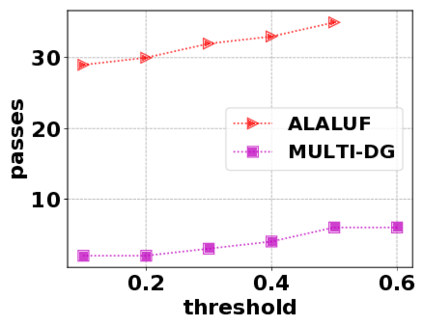
In this paper, we consider the optimization problem \scpl (\scp), which is to find a minimum cost subset of a ground set $U$ such that the value of a submodular function $f$ is above a threshold $\tau$. In contrast to most existing work on \scp, it is not assumed that $f$ is monotone. Two bicriteria approximation algorithms are presented for \scp that, for input parameter $0 < \epsilon < 1$, give $O( 1 / \epsilon^2 )$ ratio to the optimal cost and ensures the function $f$ is at least $\tau(1 - \epsilon)/2$. A lower bound shows that under the value query model shows that no polynomial-time algorithm can ensure that $f$ is larger than $\tau/2$. Further, the algorithms presented are scalable to large data sets, processing the ground set in a stream. Similar algorithms developed for \scp also work for the related optimization problem of \smpl (\smp). Finally, the algorithms are demonstrated to be effective in experiments involving graph cut and data summarization functions.
翻译:在本文中,我们考虑了优化问题 \ scpl (\ scp), 即找到一个最低成本子集, 即找到一个最低成本子集, 地价为1美元, 这样子模块函数的值将超过阈值$\ tau$。 与大多数关于\ scp 的现有工作相比, 假设不是美元是单数。 为\ scp 提供了两种双标准近似算法, 对于输入参数 $0 < persilon < 1 美元, 给 $( 1 /\ epsilon% 2 ) 与最佳成本的比值, 并确保子模块函数的值值至少为$\ tau( 1 -\ \ eepslon) / /2 美元。 较低约束值显示, 在价值查询模型中, 没有多元时间算法可以确保$大于 $\\ tau/2 美元。 此外, 提供的算法可以测量大型数据集, 在流中处理地面组中, 开发的类似算法, 也显示为相关最优化函数 。