Stochastic Saddle-Point Optimization for Wasserstein Barycenters

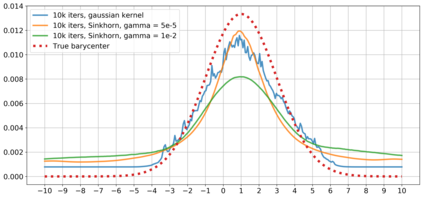
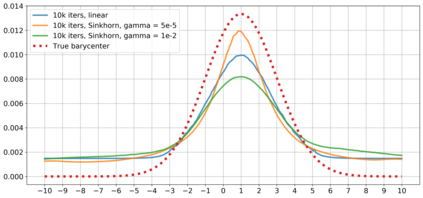
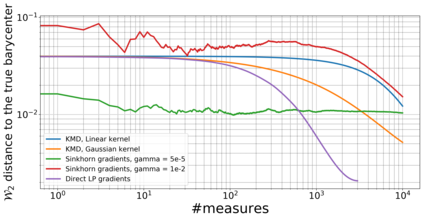
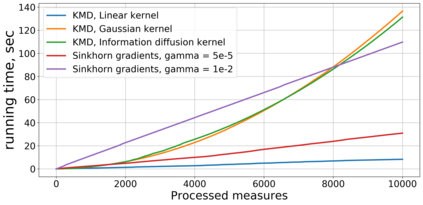
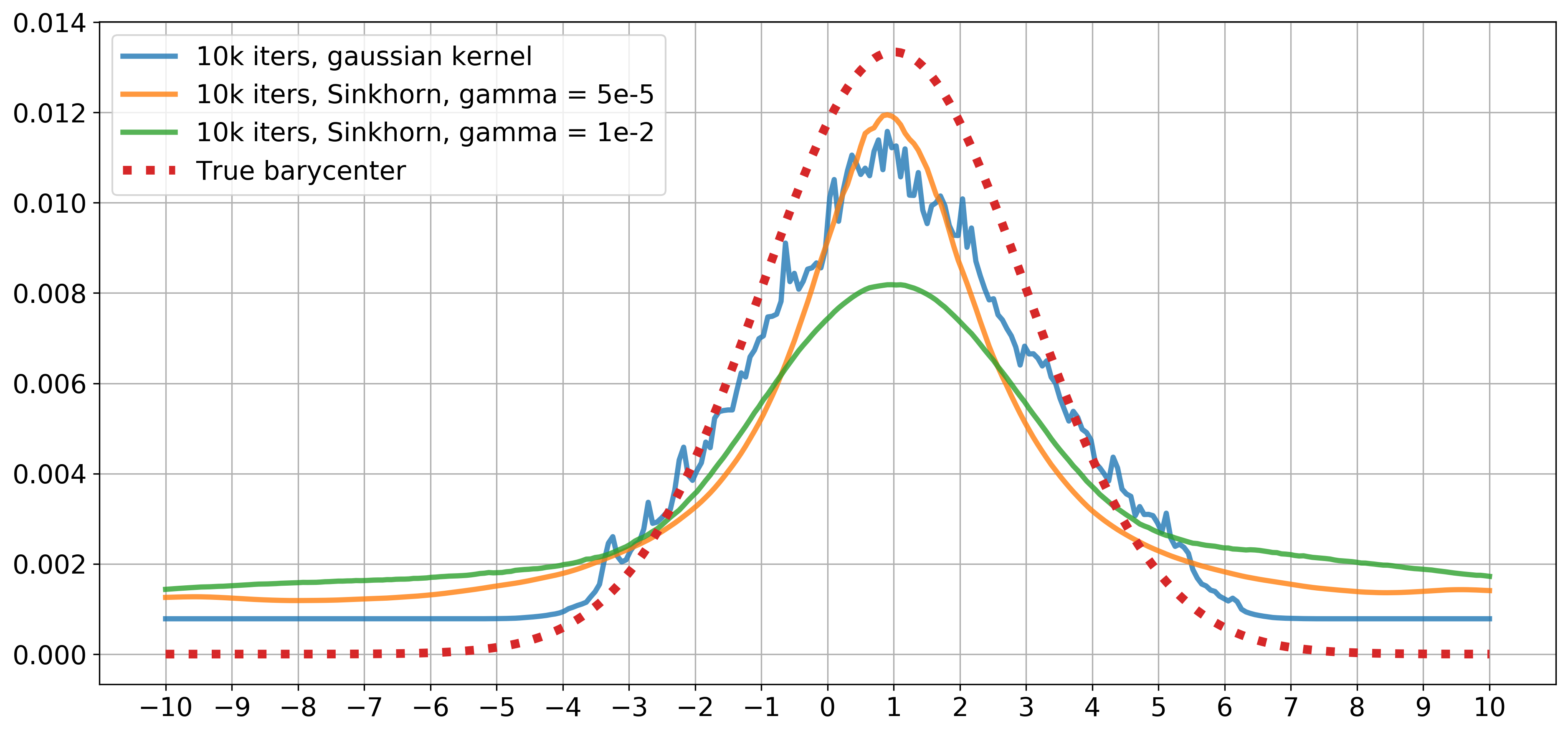
We consider population Wasserstein barycenter problem for random probability measures supported on a finite set of points and generated by an online stream of data. This leads to a complicated stochastic optimization problem where the objective is given as an expectation of a function given as a solution to random optimization problem. We employ the structure of the problem and obtain a convex-concave stochastic saddle-point reformulation of this problem. In the setting when the distribution of random probability measures is discrete, we propose a stochastic optimization algorithm and estimate its complexity. The second result, based on kernel methods, extends the previous one to the arbitrary distribution of random probability measures. Moreover, this new algorithm has a total complexity better than the Stochastic Approximation approach combined with the Sinkhorn algorithm in many cases. We also illustrate our developments by a series of numerical experiments.