Contributions to Large Scale Bayesian Inference and Adversarial Machine Learning

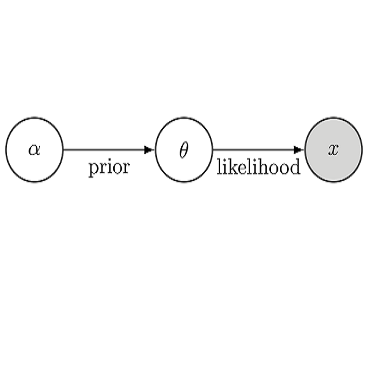
The rampant adoption of ML methodologies has revealed that models are usually adopted to make decisions without taking into account the uncertainties in their predictions. More critically, they can be vulnerable to adversarial examples. Thus, we believe that developing ML systems that take into account predictive uncertainties and are robust against adversarial examples is a must for critical, real-world tasks. We start with a case study in retailing. We propose a robust implementation of the Nerlove-Arrow model using a Bayesian structural time series model. Its Bayesian nature facilitates incorporating prior information reflecting the manager's views, which can be updated with relevant data. However, this case adopted classical Bayesian techniques, such as the Gibbs sampler. Nowadays, the ML landscape is pervaded with neural networks and this chapter also surveys current developments in this sub-field. Then, we tackle the problem of scaling Bayesian inference to complex models and large data regimes. In the first part, we propose a unifying view of two different Bayesian inference algorithms, Stochastic Gradient Markov Chain Monte Carlo (SG-MCMC) and Stein Variational Gradient Descent (SVGD), leading to improved and efficient novel sampling schemes. In the second part, we develop a framework to boost the efficiency of Bayesian inference in probabilistic models by embedding a Markov chain sampler within a variational posterior approximation. After that, we present an alternative perspective on adversarial classification based on adversarial risk analysis, and leveraging the scalable Bayesian approaches from chapter 2. In chapter 4 we turn to reinforcement learning, introducing Threatened Markov Decision Processes, showing the benefits of accounting for adversaries in RL while the agent learns.