Beyond Neyman-Pearson

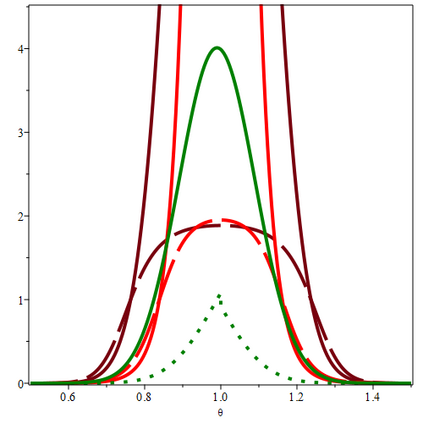
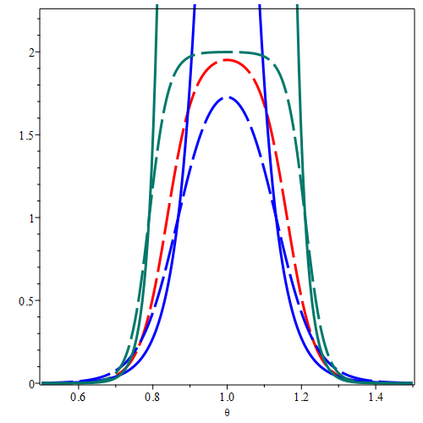
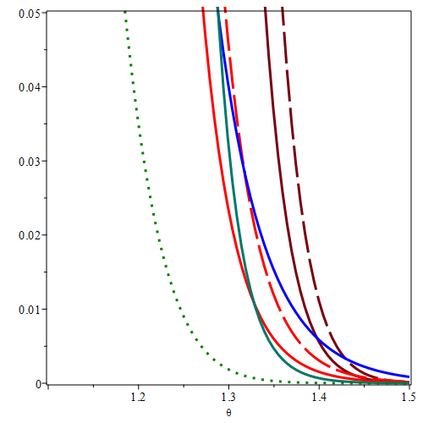
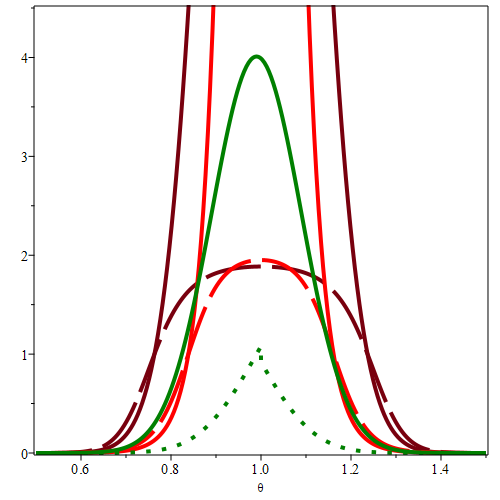
A standard practice in statistical hypothesis testing is to mention the p-value alongside the accept/reject decision. We show the advantages of mentioning an e-value instead. With p-values, we cannot use an extreme observation (e.g. $p \ll \alpha$) for getting better frequentist decisions. With e-values we can, since they provide Type-I risk control in a generalized Neyman-Pearson setting with the decision task (a general loss function) determined post-hoc, after observation of the data - thereby providing a handle on "roving $\alpha$'s". When Type-II risks are taken into consideration, the only admissible decision rules in the post-hoc setting turn out to be e-value-based. We also propose to replace confidence intervals and distributions by the *e-posterior*, which provides valid post-hoc frequentist uncertainty assessments irrespective of prior correctness: if the prior is chosen badly, e-intervals get wide rather than wrong, suggesting the e-posterior minimax decision rule as a safer alternative for Bayes decisions. The resulting "quasi-conditional paradigm" addresses foundational and practical issues in statistical inference.