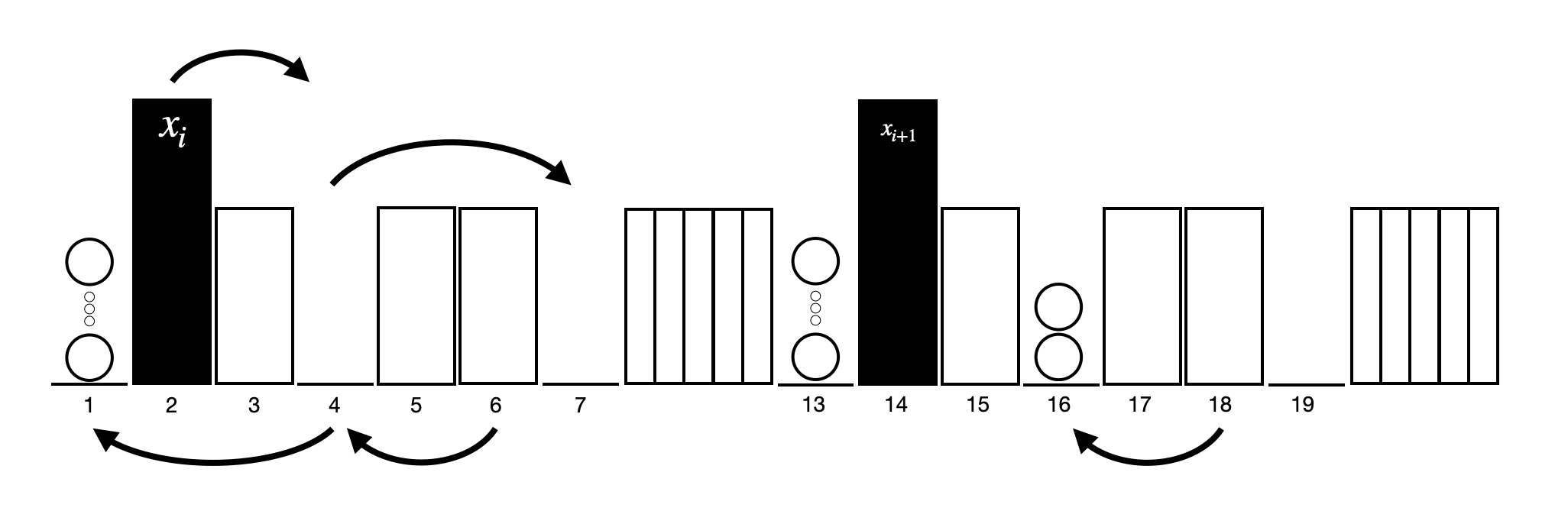
We study the computational complexity of the popular board game backgammon. We show that deciding whether a player can win from a given board configuration is NP-Hard, PSPACE-Hard, and EXPTIME-Hard under different settings of known and unknown opponents' strategies and dice rolls. Our work answers an open question posed by Erik Demaine in 2001. In particular, for the real life setting where the opponent's strategy and dice rolls are unknown, we prove that determining whether a player can win is EXPTIME-Hard. Interestingly, it is not clear what complexity class strictly contains each problem we consider because backgammon games can theoretically continue indefinitely as a result of the capture rule.
翻译:我们研究了流行棋盘双陆棋游戏的计算复杂性。 我们显示,决定玩家能否从特定棋盘配置中获胜的是NP-Hard、PSPACE-Hard和EXPTIME-Hard, 在不同已知和未知的对手策略和骰子卷的环境下。 我们的工作回答了Erik Demaine在2001年提出的一个未决问题。 特别是,对于对手策略和骰子卷未知的真实生活环境,我们证明确定玩家能否赢的游戏是EXPTIME-Hard。 有趣的是,我们所考虑的每一个问题都严格包含在什么复杂等级,并不清楚,因为基于捕获规则,后洋游戏理论上可以无限期地持续。