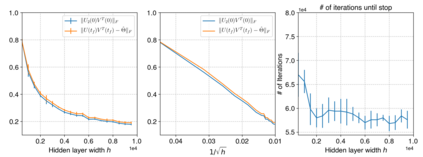
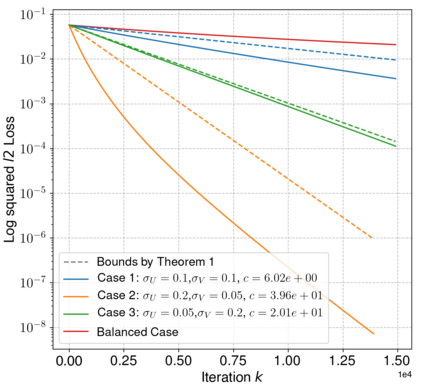
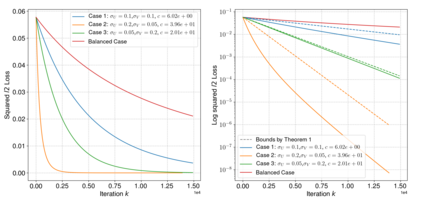
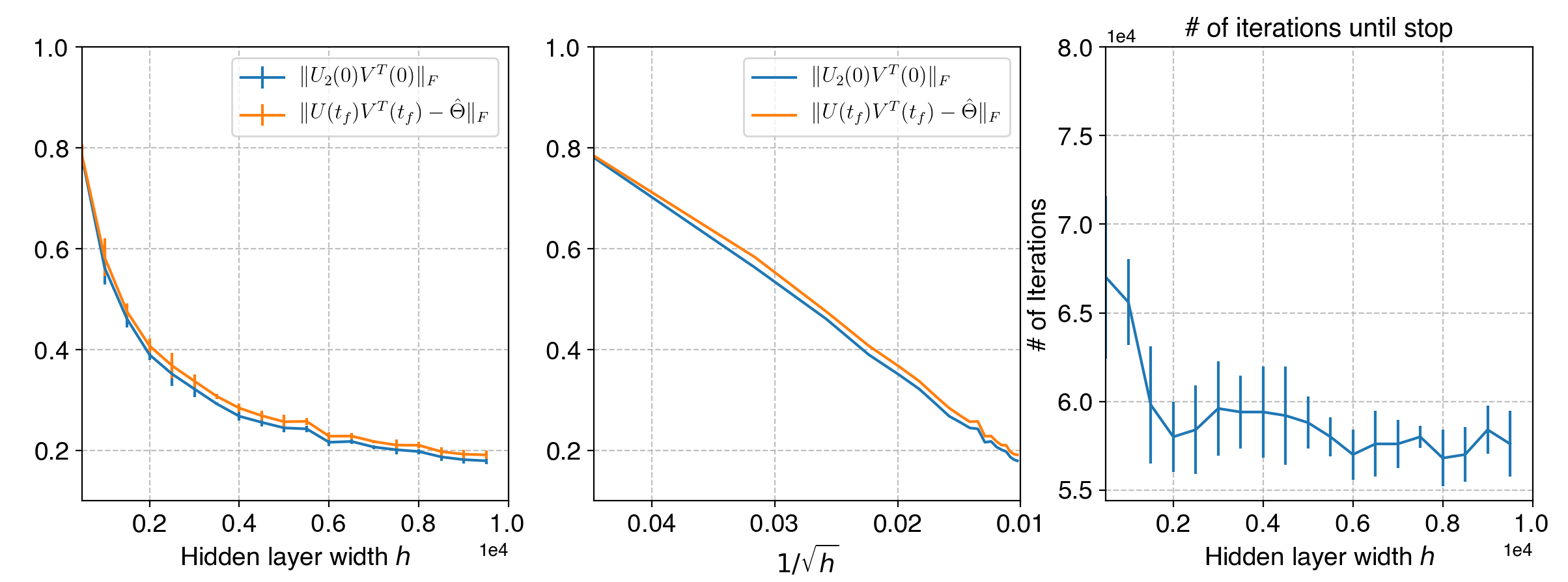
Neural networks trained via gradient descent with random initialization and without any regularization enjoy good generalization performance in practice despite being highly overparametrized. A promising direction to explain this phenomenon is to study how initialization and overparametrization affect convergence and implicit bias of training algorithms. In this paper, we present a novel analysis of single-hidden-layer linear networks trained under gradient flow, which connects initialization, optimization, and overparametrization. Firstly, we show that the squared loss converges exponentially to its optimum at a rate that depends on the level of imbalance of the initialization. Secondly, we show that proper initialization constrains the dynamics of the network parameters to lie within an invariant set. In turn, minimizing the loss over this set leads to the min-norm solution. Finally, we show that large hidden layer width, together with (properly scaled) random initialization, ensures proximity to such an invariant set during training, allowing us to derive a novel non-asymptotic upper-bound on the distance between the trained network and the min-norm solution.
翻译:通过梯度下降培训的神经网络,随机初始化,没有正规化,尽管高度偏差,但通过梯度下降而培训的神经网络在实践中享有良好的概括性表现。解释这一现象的一个很有希望的方向是研究初始化和超平衡化如何影响培训算法的趋同和隐含偏差。在本文中,我们介绍了对在梯度流下培训的单隐藏层线网络的新分析,这种网络将初始化、优化和过度平衡联系起来。首先,我们表明,平方值损失成倍接近其最佳程度,其速度取决于初始化的不平衡程度。第二,我们表明,适当的初始化限制了网络参数的动态,使其处于变异状态中。反过来,最大限度地减少这一组的损耗导致最小度溶液。最后,我们表明,巨大的隐藏层宽,加上(适当缩放的)随机初始化,确保了在培训期间与这种变异性设置的距离接近,从而使我们能够在经过训练的网络和微调溶液的距离上找到一个新的非被动的上限。