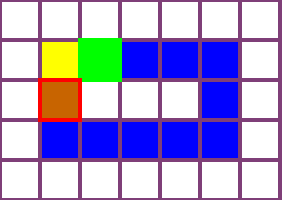
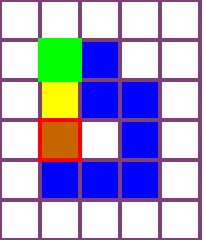
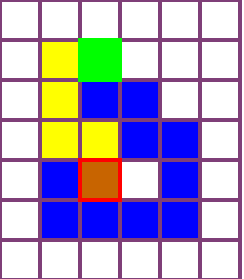
Edge-connected configurations of squares are a common model for modular robots in two dimensions. A well-established way to reconfigure such modular robots are so-called sliding moves. Dumitrescu and Pach [Graphs and Combinatorics, 2006] proved that it is always possible to reconfigure one edge-connected configuration of $n$ squares into any other using at most $O(n^2)$ sliding moves, while keeping the configuration connected at all times. For certain configurations $\Omega(n^2)$ sliding moves are necessary. However, significantly fewer moves may be sufficient. In this paper we present a novel input-sensitive in-place algorithm which requires only $O(\bar{P} n)$ sliding moves to transform one configuration into the other, where $\bar{P}$ is the maximum perimeter of the respective bounding boxes. Our Gather&Compact algorithm is built on the basic principle that well-connected components of modular robots can be transformed efficiently. Hence we iteratively increase the connectivity within a configuration, to finally arrive at a single solid $xy$-monotone component. We implemented Gather&Compact and compared it experimentally to the in-place modification by Moreno and Sacrist\'an [EuroCG 2020] of the Dumitrescu and Pach algorithm (MSDP). Our experiments show that Gather&Compact consistently outperforms MSDP by a significant margin, on all types of square configurations.
翻译:连接方形的边际配置是模块机器人在两个维度上的一种常见模式。 重塑这些模块机器人的既定方式是所谓的滑动动作。 Dumitrescu 和 Pach [ Graphs 和 Compatoric, 2006] 证明, 总是有可能将一个连接边际的方形配置重新配置为以美元为最大值的绑定框的最大范围。 我们的集合和组合算法建立在基本原理之上, 即模块机器人的连接良好的组件可以有效转换。 然而, 某些配置 $\ omega (n2) 的滑动是必要的。 但是, 移动可能足够少得多。 在本文中, 我们展示了一个新的对投入敏感的本地算法, 只需要$(\ bar{ P} n) 和 Pach[ Pacha], 将一个配置转换成另一个, $\ bar{ P} 的最大范围。 我们的集合和复合算法建立在一个基本原则上, 模块机器人的连接良好的构件可以有效转换。 因此, 我们反复增加一个配置内部的连接, 最终到达一个单一的基质 $xy$- motone 的配置, 到一个单一的基型的配置。 我们的SAR- groachdeal- trabial- greal acudestrationalateal extobismal acumental view viewdal view view view views view view 。