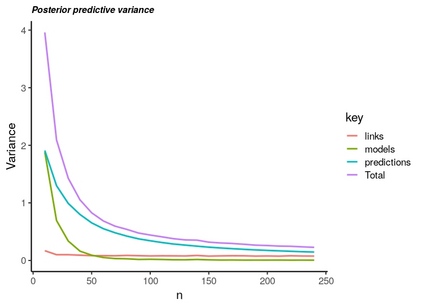
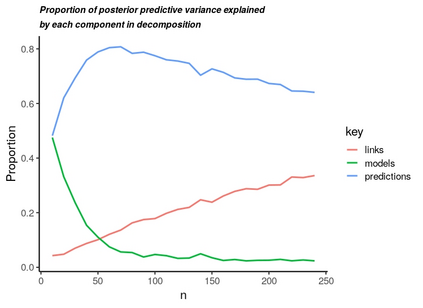
We give a decomposition of the posterior predictive variance using the law of total variance and conditioning on a finite dimensional discrete random variable. This random variable summarizes various features of modeling that are used to form the prediction for a future outcome. Then, we test which terms in this decomposition are small enough to ignore. This allows us identify which of the discrete random variables are most important to prediction intervals. The terms in the decomposition admit interpretations based on conditional means and variances and are analogous to the terms in a Cochran's theorem decomposition of squared error often used in analysis of variance. Thus, the modeling features are treated as factors in completely randomized design. In cases where there are multiple decompositions we suggest choosing the one that that gives the best predictive coverage with the smallest variance.
翻译:我们使用完全差异定律对后天预测差异进行分解, 并以一个有限维度离散随机变量为条件。 这个随机变量概述了用于预测未来结果的模型的各种特征。 然后, 我们测试这个分解中的哪个术语小到足以忽略。 这让我们可以确定哪些离散随机变量对预测间隔最为重要。 分解中的术语允许基于有条件手段和差异进行解释, 并类似于在分析差异时常用的Cochran的方位变异术语。 因此, 模型特征被当作完全随机设计中的因素处理。 在存在多种分解因素的情况下, 我们建议选择一个能够以最小差异提供最佳预测覆盖的参数 。