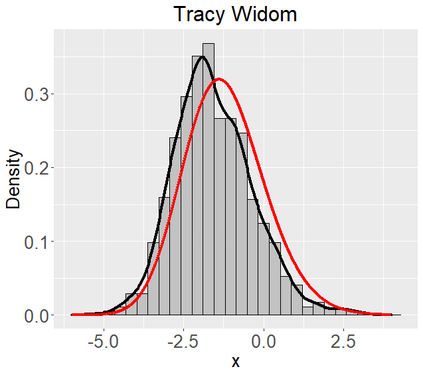
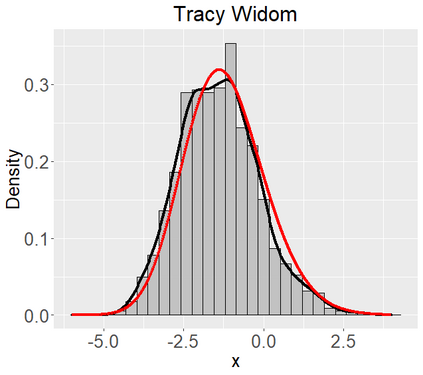
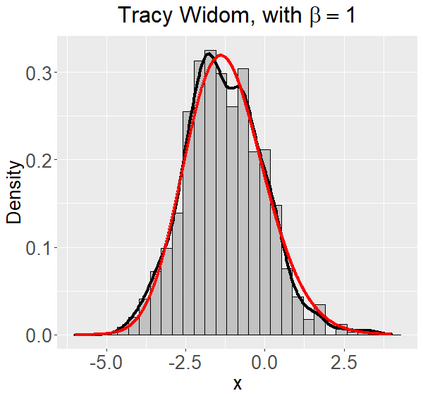
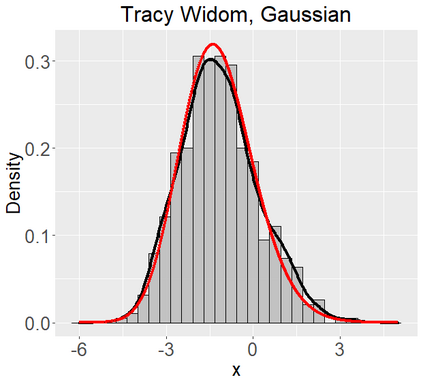
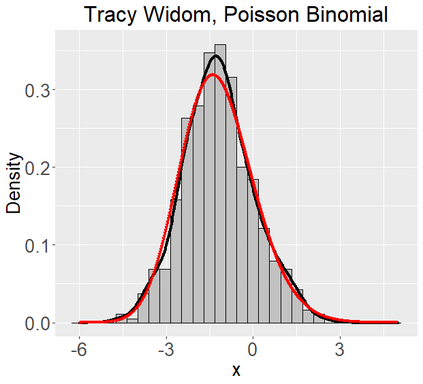
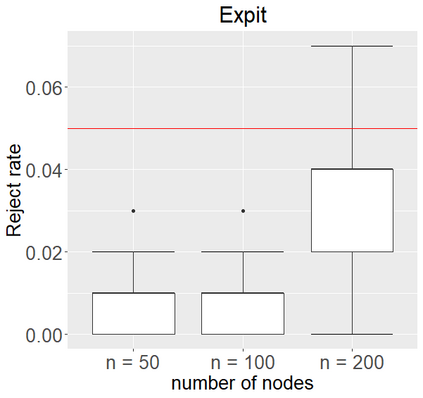
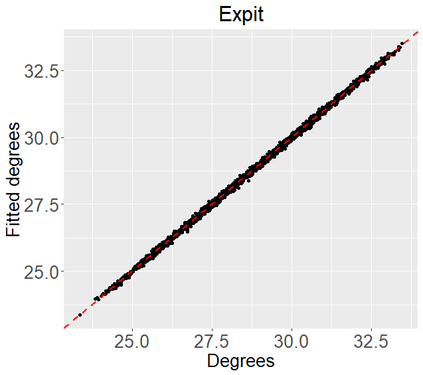
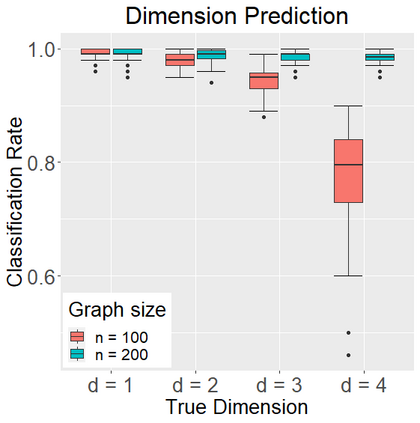
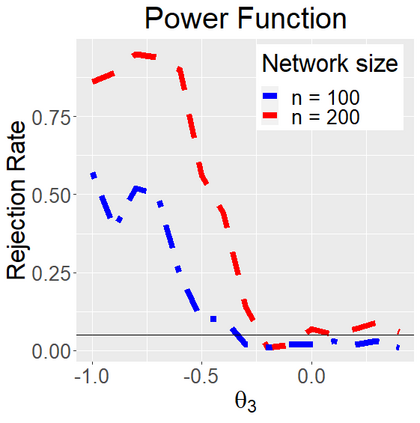
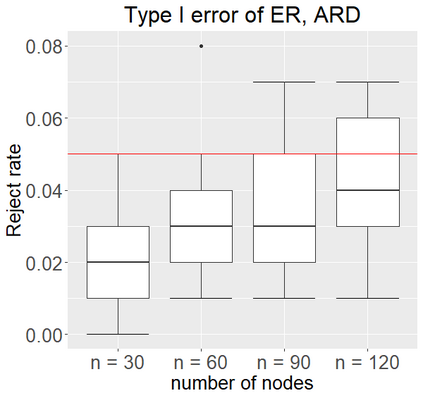
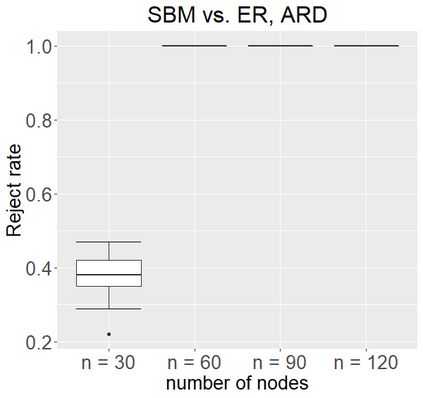
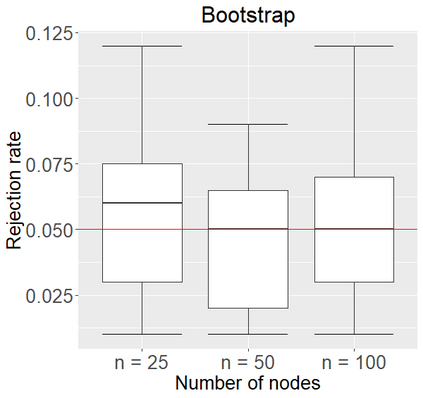
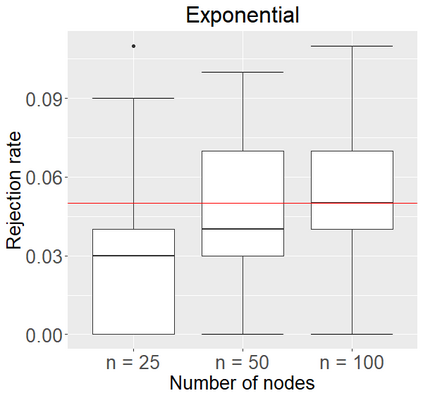
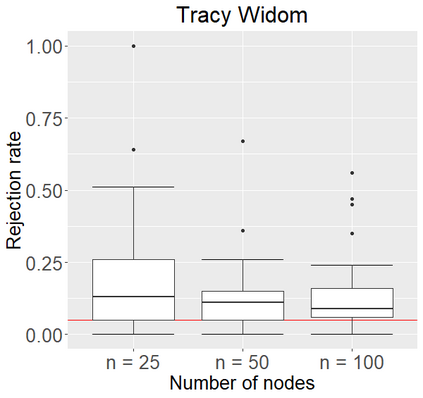
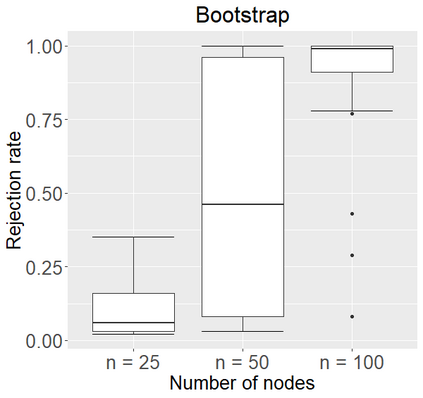
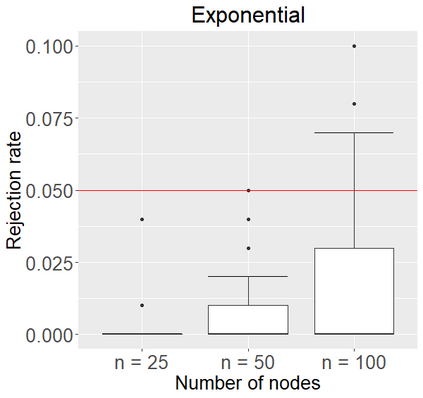
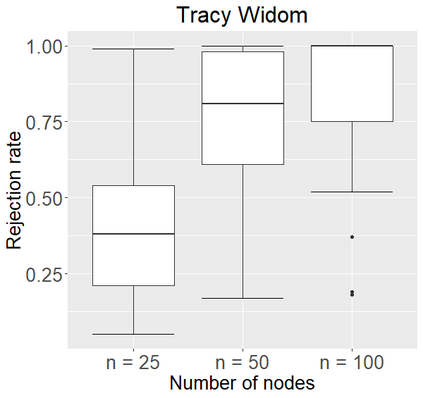
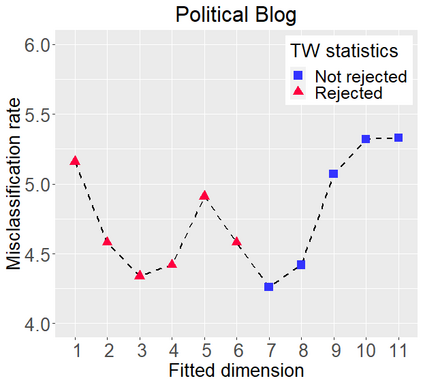
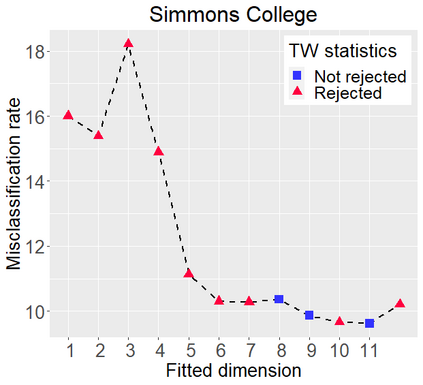
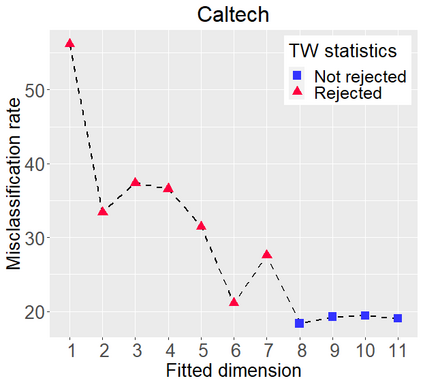
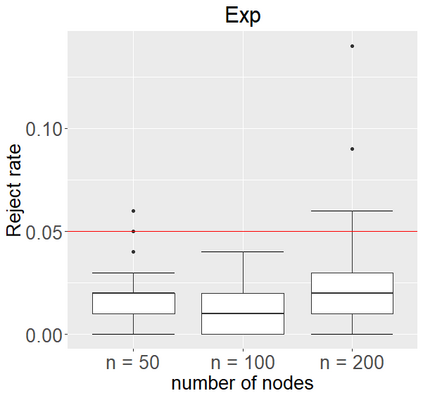
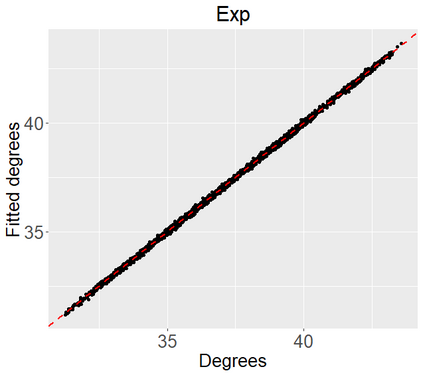
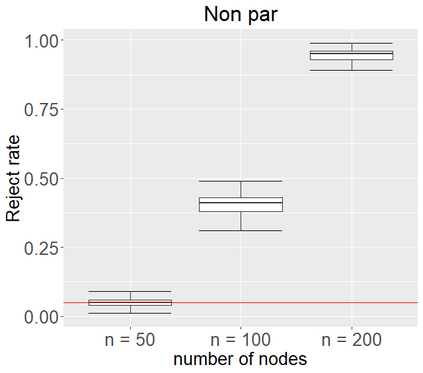
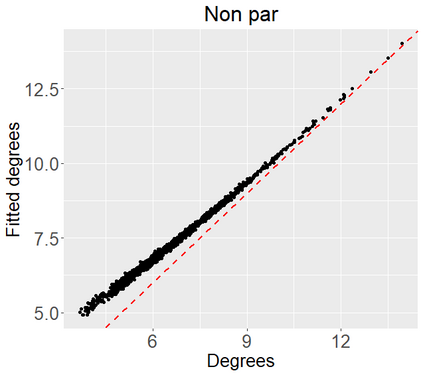
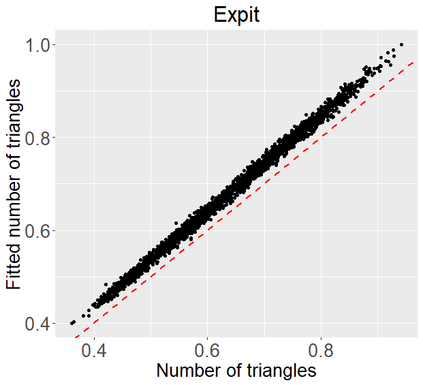
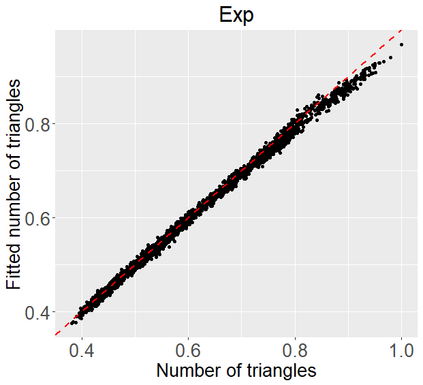
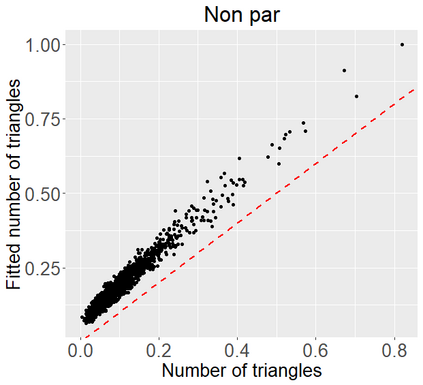
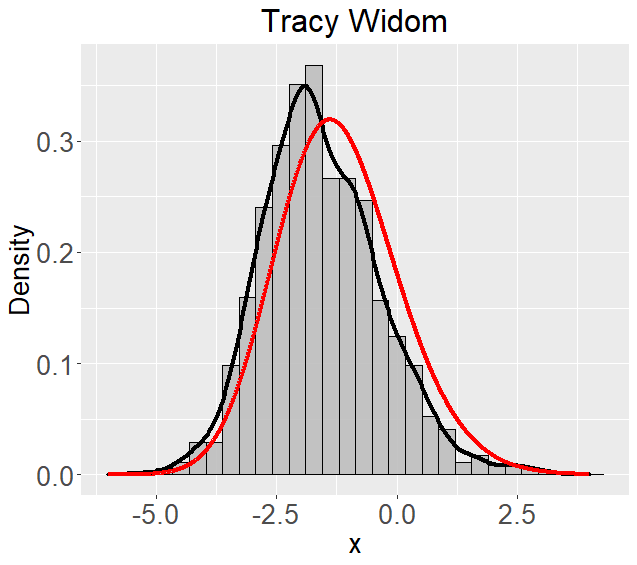
Networks describe the, often complex, relationships between individual actors. In this work, we address the question of how to determine whether a parametric model, such as a stochastic block model or latent space model, fits a dataset well and will extrapolate to similar data. We use recent results in random matrix theory to derive a general goodness-of-fit test for dyadic data. We show that our method, when applied to a specific model of interest, provides an straightforward, computationally fast way of selecting parameters in a number of commonly used network models. For example, we show how to select the dimension of the latent space in latent space models. Unlike other network goodness-of-fit methods, our general approach does not require simulating from a candidate parametric model, which can be cumbersome with large graphs, and eliminates the need to choose a particular set of statistics on the graph for comparison. It also allows us to perform goodness-of-fit tests on partial network data, such as Aggregated Relational Data. We show with simulations that our method performs well in many situations of interest. We analyze several empirically relevant networks and show that our method leads to improved community detection algorithms. R code to implement our method is available on Github.
翻译:网络描述个体行为者之间往往十分复杂的关系。 在这项工作中,我们处理如何确定一个参数模型,例如随机区块模型或潜潜空空间模型,是否适合数据集,如何对数据集进行完善,如何推断类似数据。我们使用随机矩阵理论的最新结果来得出对dydic数据进行一般的优异测试。我们表明,我们的方法,如果应用到一个具体的兴趣模型,就能为选择一些常用网络模型中的参数提供一个简单、快速的计算方法。例如,我们展示了如何选择潜在空间模型中潜在空间的维度。与其他网络的优异方法不同,我们的一般方法并不要求从候选的参数模型中模拟,而该模型可能与大图表不相干,并消除了在图表上选择一套特定统计数据以供比较的必要性。我们还可以对部分网络数据,例如综合关系数据进行优异的测试。我们通过模拟来显示我们的方法在许多感兴趣的情况下都表现良好。我们分析了几个与实验相关的网络,并展示了我们的方法可以用来改进社区测算法的方法。