Bounds for Privacy-Utility Trade-off with Per-letter Privacy Constraints and Non-zero Leakage

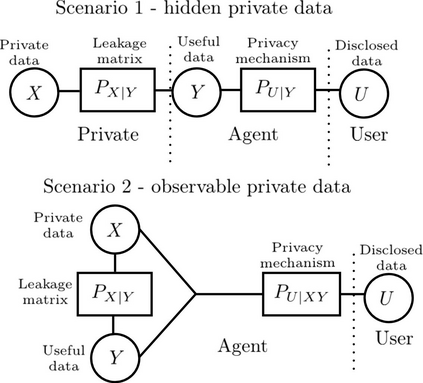
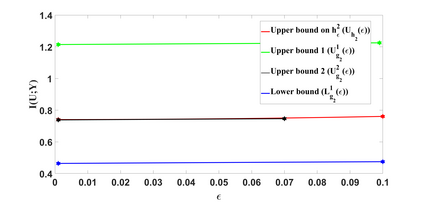
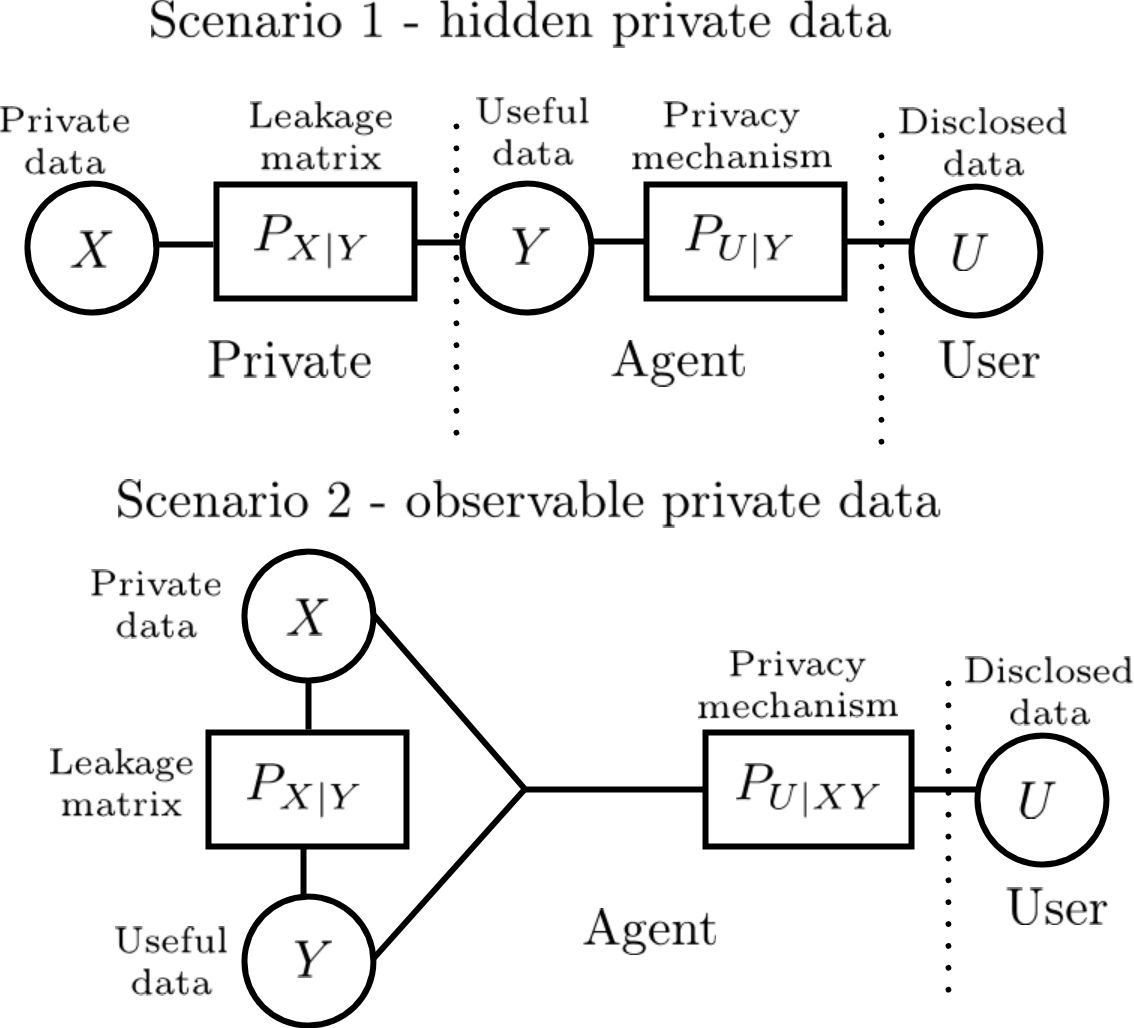
An information theoretic privacy mechanism design problem for two scenarios is studied where the private data is either hidden or observable. In each scenario, privacy leakage constraints are considered using two different measures. In these scenarios the private data is hidden or observable. In the first scenario, an agent observes useful data $Y$ that is correlated with private data $X$, and wishes to disclose the useful information to a user. A privacy mechanism is designed to generate disclosed data $U$ which maximizes the revealed information about $Y$ while satisfying a per-letter privacy constraint. In the second scenario, the agent has additionally access to the private data. First, the Functional Representation Lemma and Strong Functional Representation Lemma are extended by relaxing the independence condition to find a lower bound considering the second scenario. Next, lower bounds as well as upper bounds on privacy-utility trade-off are derived for both scenarios. In particular, for the case where $X$ is deterministic function of $Y$, we show that our upper and lower bounds are asymptotically optimal considering the first scenario.