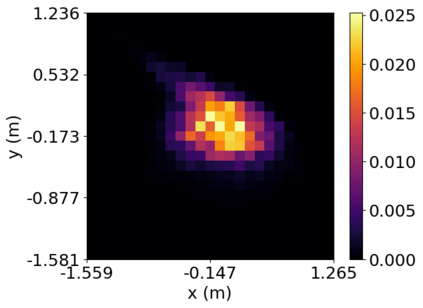
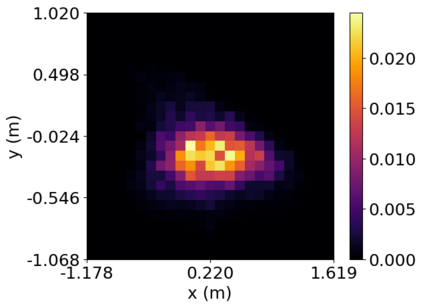
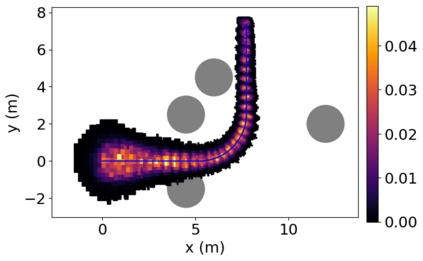
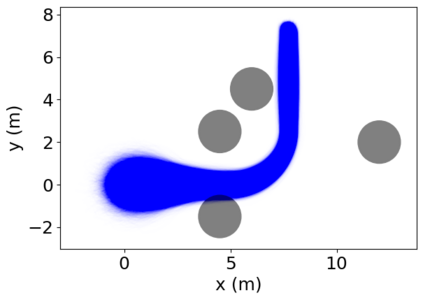
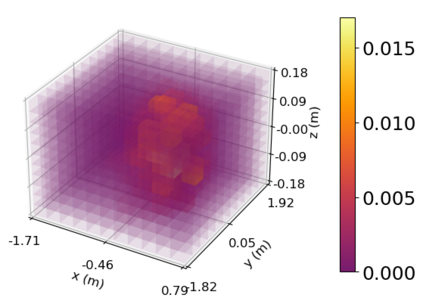
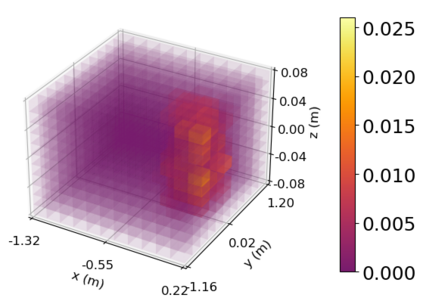
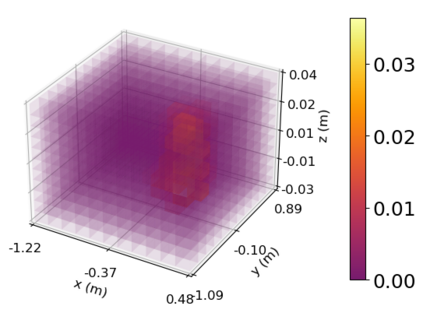
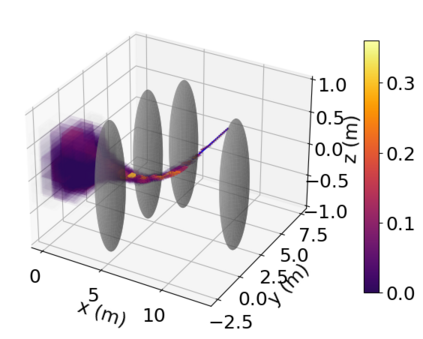
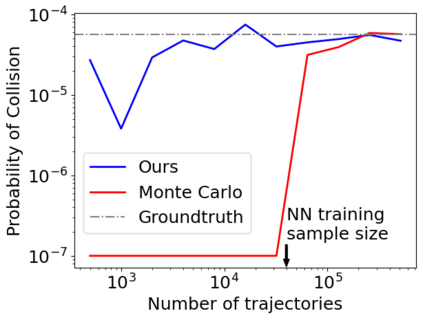
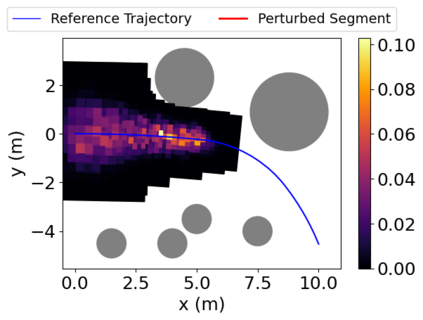
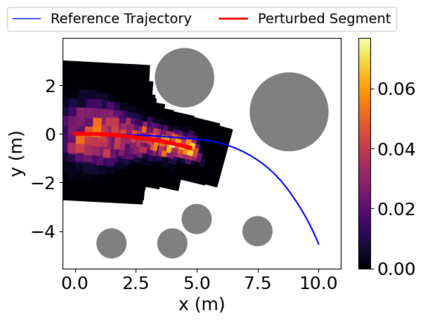
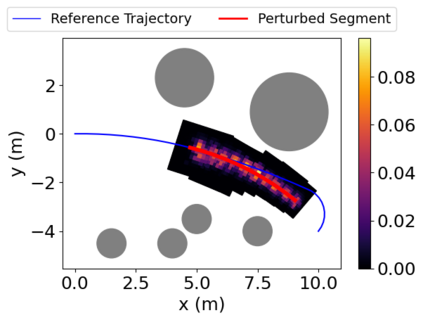
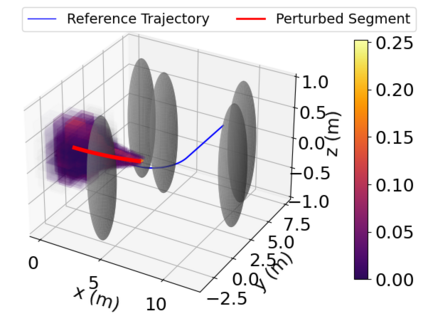
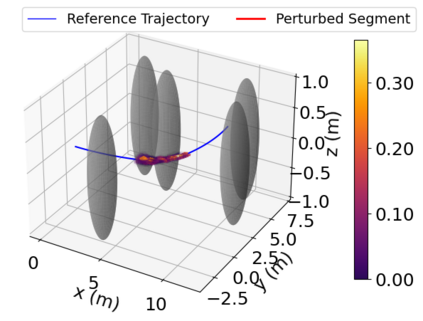
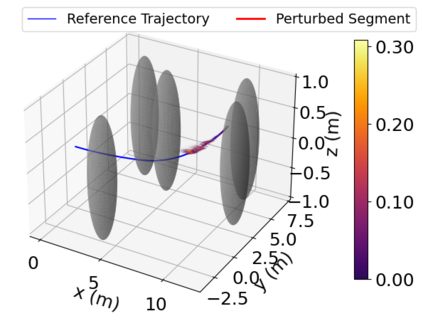
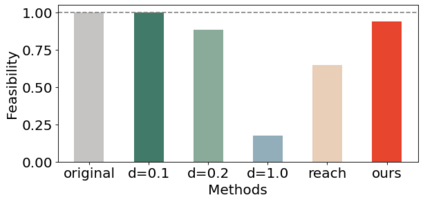
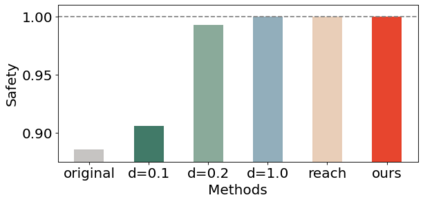
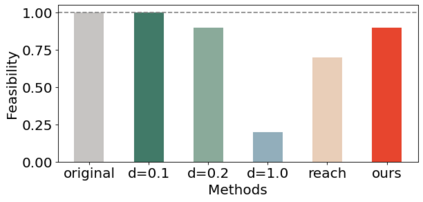
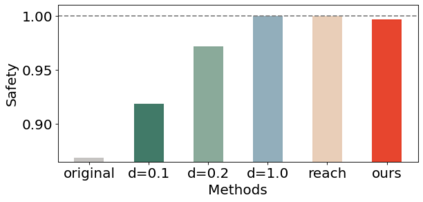
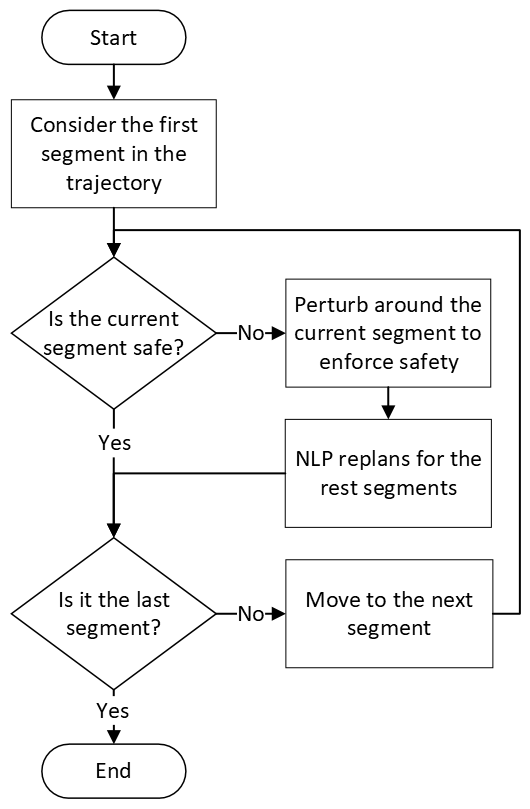
Density of the reachable states can help understand the risk of safety-critical systems, especially in situations when worst-case reachability is too conservative. Recent work provides a data-driven approach to compute the density distribution of autonomous systems' forward reachable states online. In this paper, we study the use of such approach in combination with model predictive control for verifiable safe path planning under uncertainties. We first use the learned density distribution to compute the risk of collision online. If such risk exceeds the acceptable threshold, our method will plan for a new path around the previous trajectory, with the risk of collision below the threshold. Our method is well-suited to handle systems with uncertainties and complicated dynamics as our data-driven approach does not need an analytical form of the systems' dynamics and can estimate forward state density with an arbitrary initial distribution of uncertainties. We design two challenging scenarios (autonomous driving and hovercraft control) for safe motion planning in environments with obstacles under system uncertainties. We first show that our density estimation approach can reach a similar accuracy as the Monte-Carlo-based method while using only 0.01X training samples. By leveraging the estimated risk, our algorithm achieves the highest success rate in goal reaching when enforcing the safety rate above 0.99.
翻译:可获得的状态的密度密度可以帮助理解安全临界系统的风险,特别是在最差的可达性太保守的情况下。最近的工作提供了一种数据驱动方法,用以计算自动系统前可达的状态的密度分布;在本文中,我们研究如何使用这种方法,同时结合模型预测控制,以在不确定情况下进行可核查的安全路径规划;我们首先使用所学到的密度分布方法来计算在线碰撞的风险;如果这种风险超过可接受的阈值,我们的方法将计划在前一条轨道上开辟一条新的路径,其碰撞风险将低于临界值。我们的方法非常适合处理具有不确定性和复杂动态的系统,因为我们的数据驱动的方法不需要系统动态的分析形式,而且能够以任意的初步不确定性分布来估计前方的密度。我们设计了两种具有挑战性的设想(自动驾驶和悬浮器控制),以便在系统不确定存在障碍的环境中进行安全运动规划。我们首先表明,我们的密度估计方法可以达到与基于蒙特-卡洛的方法相似的精确度,同时只使用0.01X培训样品。通过利用估计的风险,我们的算法在达到目标时达到最高的成功率。