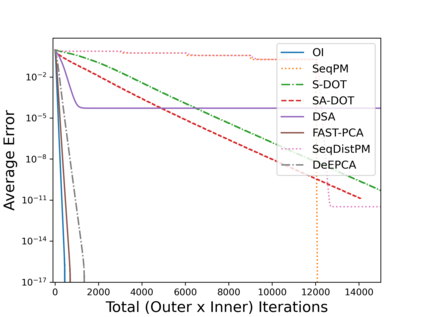
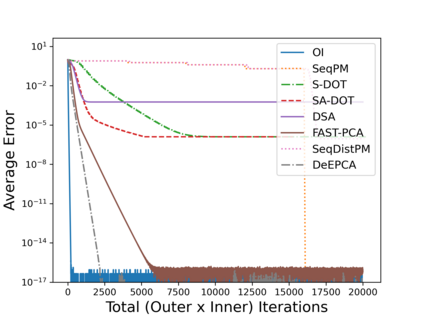
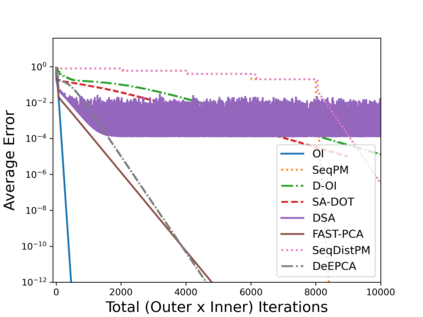
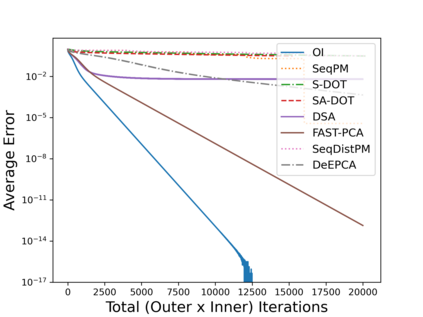
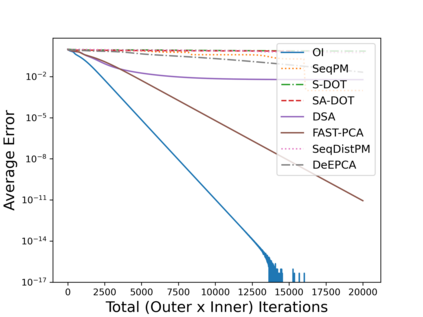
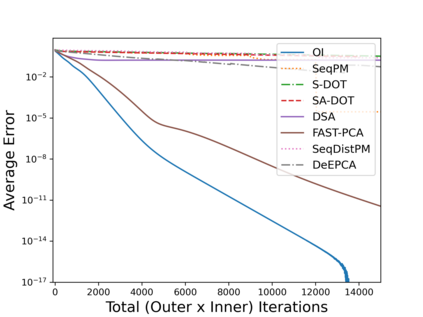
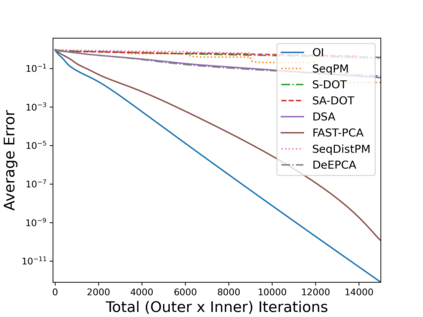
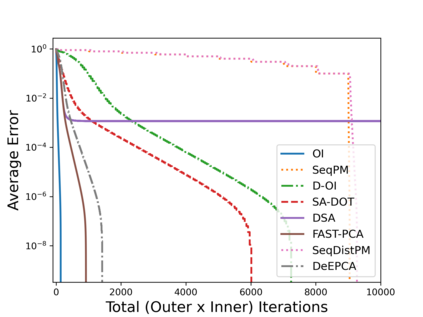
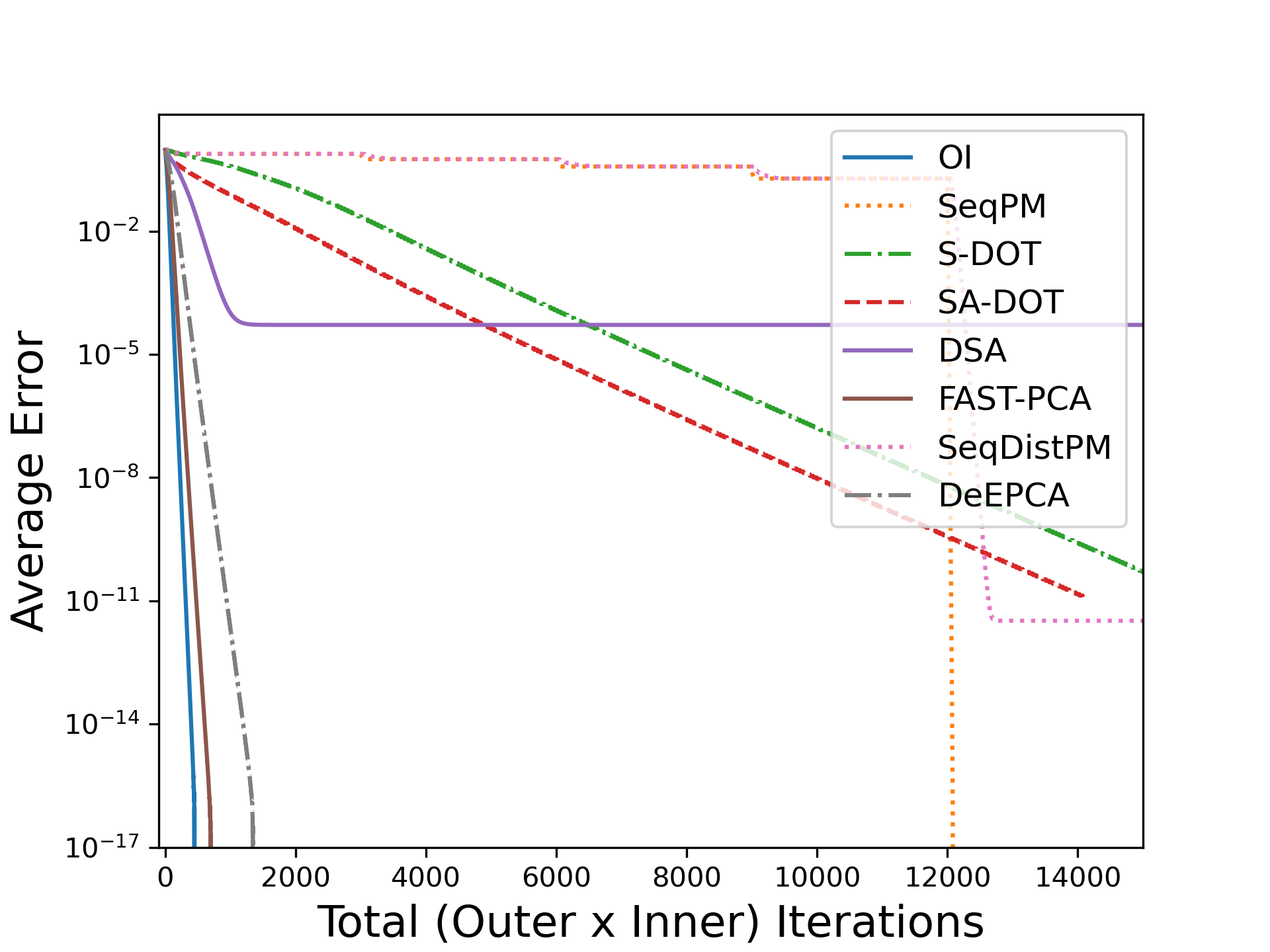
Principal Component Analysis (PCA) is a fundamental data preprocessing tool in the world of machine learning. While PCA is often thought of as a dimensionality reduction method, the purpose of PCA is actually two-fold: dimension reduction and uncorrelated feature learning. Furthermore, the enormity of the dimensions and sample size in the modern day datasets have rendered the centralized PCA solutions unusable. In that vein, this paper reconsiders the problem of PCA when data samples are distributed across nodes in an arbitrarily connected network. While a few solutions for distributed PCA exist, those either overlook the uncorrelated feature learning aspect of the PCA, tend to have high communication overhead that makes them inefficient and/or lack `exact' or `global' convergence guarantees. To overcome these aforementioned issues, this paper proposes a distributed PCA algorithm termed FAST-PCA (Fast and exAct diSTributed PCA). The proposed algorithm is efficient in terms of communication and is proven to converge linearly and exactly to the principal components, leading to dimension reduction as well as uncorrelated features. The claims are further supported by experimental results.
翻译:计算机学习世界中,主要成分分析(PCA)是一个基本的数据处理工具,在机器学习世界中,PAC常常被视为一种减少维度的方法,而PAC的目的实际上是双重的:尺寸减少和不相干的特点学习;此外,现代数据集的尺寸和抽样规模之大,使得中央中央化的CPA解决办法无法使用。在这方面,本文件重新考虑了在任意连接的网络中将数据样品分布在一个节点上时CPA的问题。虽然有关于分布式CPA的少数解决办法,但这些办法要么忽略了CPA的不相干的特点学习方面,但往往具有很高的通信间接费用,使其效率低下和/或缺乏“实际”或“全球”的汇合保证。为了克服上述问题,本文件建议采用一个分布式的CPA算法,称为FAST-PCA(Fast and ex Affact diSTbried CPA)(Fast and exact distritation distritation distrital) 。拟议的算法在通信方面是有效的,并被证明可以线性地和精确地与主要组成部分相交汇,导致尺寸的尺寸减少和不相关的特征。这些索赔得到进一步得到实验结果的支持。