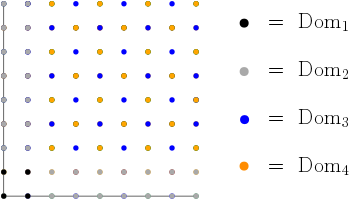
We classify the functions $f:\mathbb{N}^2 \rightarrow \mathbb{N}$ which are stably computable by output-oblivious Stochastic Chemical Reaction Networks (CRNs), i.e., systems of reactions in which output species are never reactants. While it is known that precisely the semilinear functions are stably computable by CRNs, such CRNs sometimes rely on initially producing too many output species and then consuming the excess in order to reach a correct stable state. These CRNs may be difficult to integrate into larger systems: if the output of a CRN $\mathcal{C}$ becomes the input to a downstream CRN $\mathcal{C}'$, then $\mathcal{C}'$ could inadvertently consume too many outputs before $\mathcal{C}$ stabilizes. If, on the other hand, $\mathcal{C}$ is output-oblivious then $\mathcal{C}'$ may consume $\mathcal{C}$'s output as soon as it is available. In this work we prove that a semilinear function $f:\mathbb{N}^2 \rightarrow \mathbb{N}$ is stably computable by an output-oblivious CRN with a leader if and only if it is both increasing and either grid-affine (intuitively, its domains are congruence classes), or the minimum of a finite set of fissure functions (intuitively, functions behaving like the min function).
翻译:我们分类函数 $f:\ mathbb{N ⁇ 2\rightrow \ mathb{N} 。 这些函数可能很难融入更大的系统: 如果一个输出可见的Stochastic化学反应网络(CRNs)的输出成为下游 CRCN$\mathcal{C}$, 那么$\mathcal{C} 美元可能无意中消耗太多产出, 而如果在另一边, $\mathcal{C} $是输出- oblious, 然后是美元=cal{cal{c} 可能很难融入更大的系统: 如果 CRN$\mathcal{macal{C} $的输出成为下游 CRN$\mathcal{C} 的输入, 那么$\mathcalcal{cal{c} 美元可能无意中太多产出 。 如果在另一边, $\macal=creal ral ral ral 函数是固定的 。