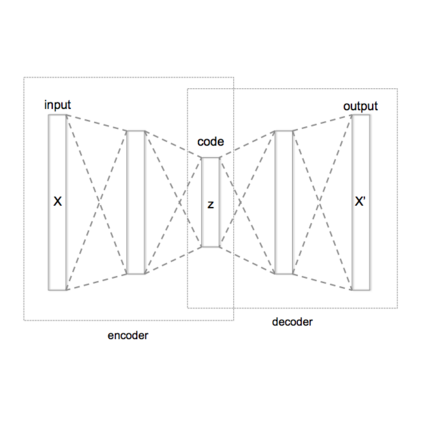
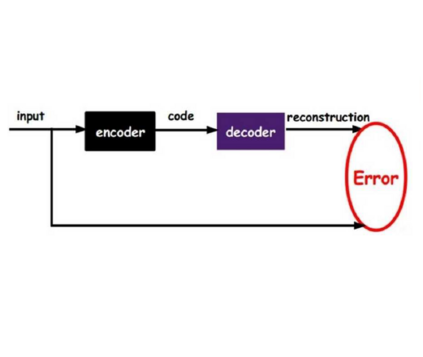
Variational autoencoder (VAE) is a very popular and well-investigated generative model vastly used in neural learning research. To leverage VAE in practical tasks dealing with a massive dataset of large dimensions it is required to deal with the difficulty of building low variance evidence lower bounds (ELBO). Markov ChainMonte Carlo (MCMC) is one of the effective approaches to tighten the ELBO for approximating the posterior distribution. Hamiltonian Variational Autoencoder(HVAE) is an effective MCMC inspired approach for constructing a low-variance ELBO which is also amenable to the reparameterization trick. In this work, we propose a Quasi-symplectic Langevin Variational autoencoder (Langevin-VAE) by incorporating the gradients information in the inference process through the Langevin dynamic. We show the effectiveness of the proposed approach by toy and real-world examples.
翻译:在神经学习研究中广泛使用的一种非常受欢迎和调查良好的基因模型(VAE)是一种非常受欢迎和调查良好的基因模型。为了利用VAE处理大量大型数据集的实际任务,需要它处理建立低差异证据下下限的困难。Markov 链-Monte Carlo(MCMC)是收紧ELBO以近似于后体分布的有效办法之一。汉密尔顿 variational Autencoder(HVAE)是一种有效的MCMC启发性方法,用以构建一种低差异ELBO,这个方法也适合重新计量的技巧。在这项工作中,我们提议通过Langevin动力将梯度信息纳入推导过程,从而形成一个“准-同步”的Langevin-VAE自动电算器(Langevin-VAE),我们通过玩具和现实世界实例展示了拟议方法的有效性。