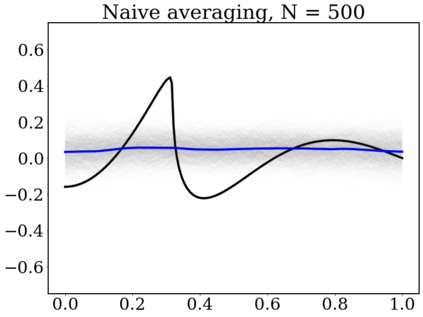
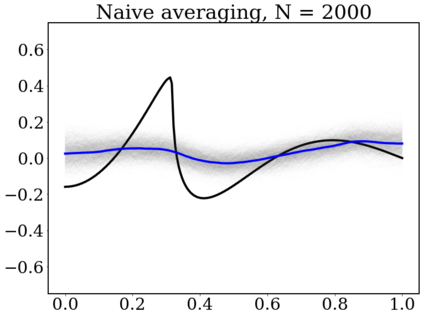
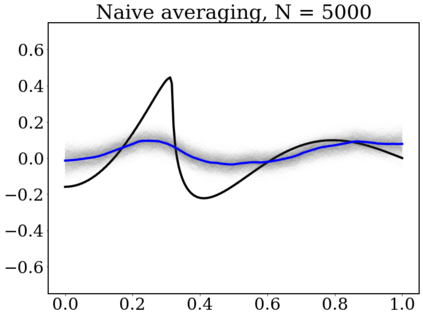
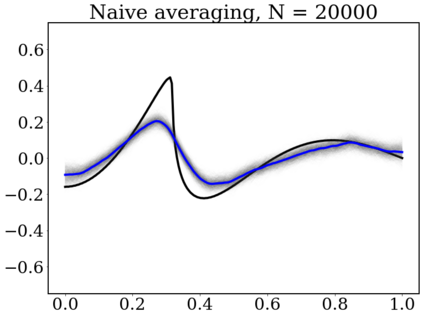
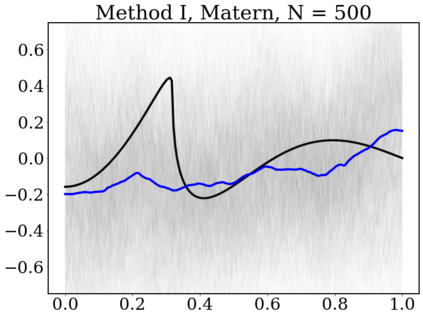
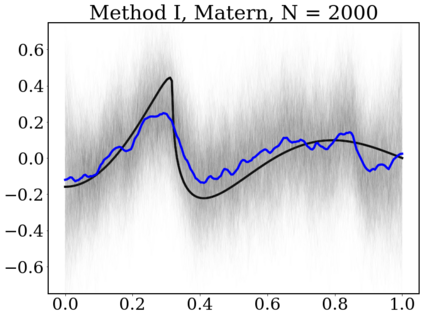
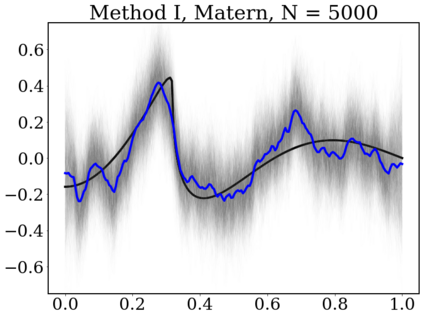
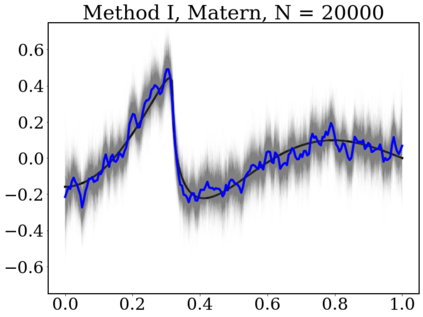
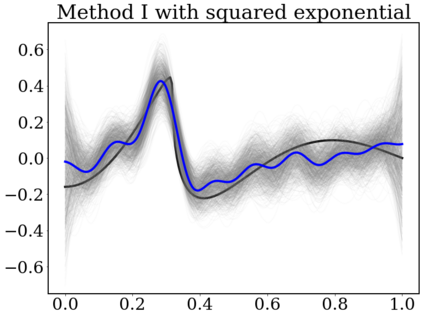
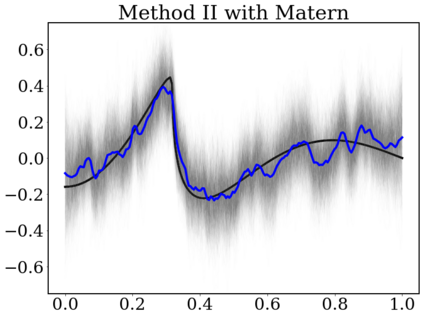
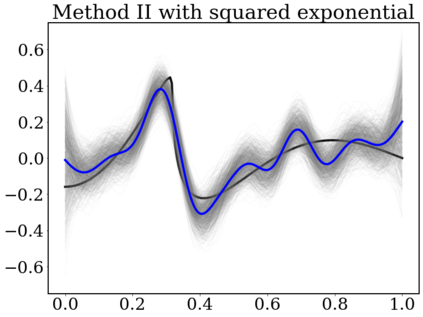
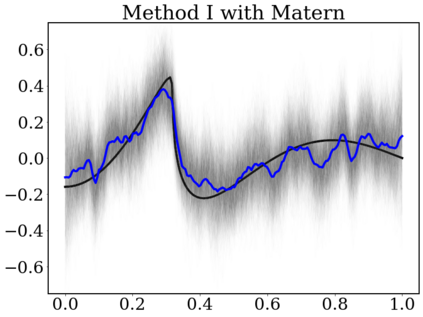
Gaussian Processes (GP) are widely used for probabilistic modeling and inference for nonparametric regression. However, their computational complexity scales cubicly with the sample size rendering them unfeasible for large data sets. To speed up the computations various distributed methods were proposed in the literature. These methods have, however, limited theoretical underpinning. In our work we derive frequentist theoretical guarantees and limitations for a range of distributed methods for general GP priors in context of the nonparametric regression model, both for recovery and uncertainty quantification. As specific examples we consider covariance kernels both with polynomially and exponentially decaying eigenvalues. We demonstrate the practical performance of the investigated approaches in a numerical study using synthetic data sets.
翻译:Gausian Processes (GP) 被广泛用于非参数回归的概率建模和推论,然而,它们的计算复杂度与样本大小不相符合,因此对于大型数据集来说不可行。为加快计算各种分布方法,文献中提出了各种分布方法,但这些方法的理论基础有限。在我们的工作中,我们从非参数回归模型中为一般GP前科的一系列分布方法获得常年理论保障和限制,用于恢复和不确定性的量化。作为具体例子,我们考虑了与多球形和指数衰减等元值的共变内核。我们在使用合成数据集进行的数字研究中展示了所调查方法的实际表现。