Counterfactual Inference of the Mean Outcome under a Convergence of Average Logging Probability

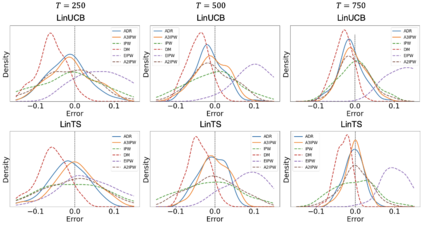
Adaptive experiments, including efficient average treatment effect estimation and multi-armed bandit algorithms, have garnered attention in various applications, such as social experiments, clinical trials, and online advertisement optimization. This paper considers estimating the mean outcome of an action from samples obtained in adaptive experiments. In causal inference, the mean outcome of an action has a crucial role, and the estimation is an essential task, where the average treatment effect estimation and off-policy value estimation are its variants. In adaptive experiments, the probability of choosing an action (logging probability) is allowed to be sequentially updated based on past observations. Due to this logging probability depending on the past observations, the samples are often not independent and identically distributed (i.i.d.), making developing an asymptotically normal estimator difficult. A typical approach for this problem is to assume that the logging probability converges in a time-invariant function. However, this assumption is restrictive in various applications, such as when the logging probability fluctuates or becomes zero at some periods. To mitigate this limitation, we propose another assumption that the average logging probability converges to a time-invariant function and show the doubly robust (DR) estimator's asymptotic normality. Under the assumption, the logging probability itself can fluctuate or be zero for some actions. We also show the empirical properties by simulations.