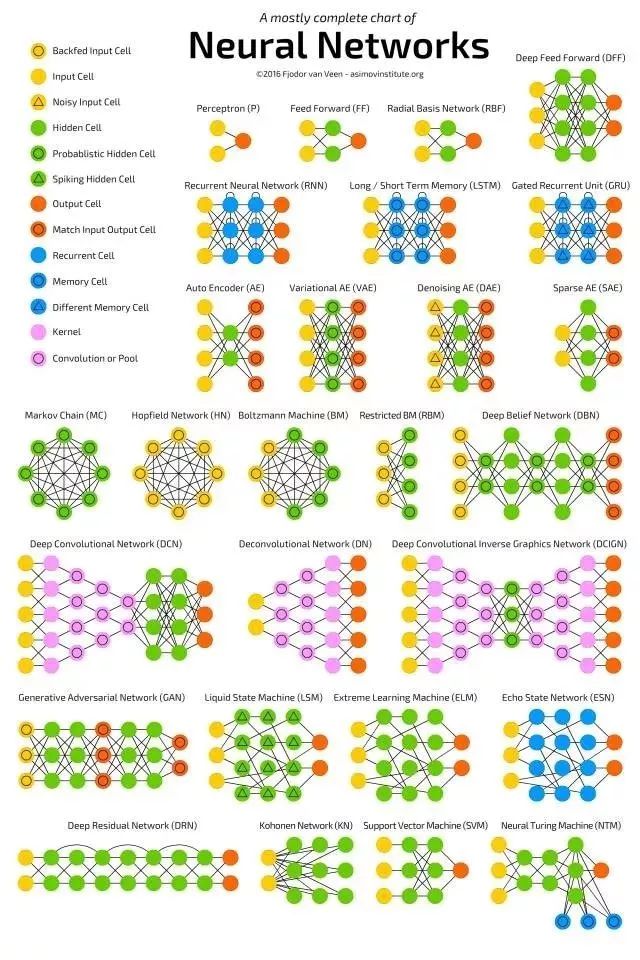
干货丨史上最好记的神经网络结构速记表（经典资源，值得收藏）

原文THE NEURAL NETWORK ZOO，出自Asimov人工智能研究所。

本文为雷锋网原创文章，如需转载请自行联系授权。

新的神经网络结构不断涌现，我们很难一一掌握。哪怕一开始只是记住所有的简称（ DCIGN，BiLSTM，DCGAN ），也会让同学们吃不消。

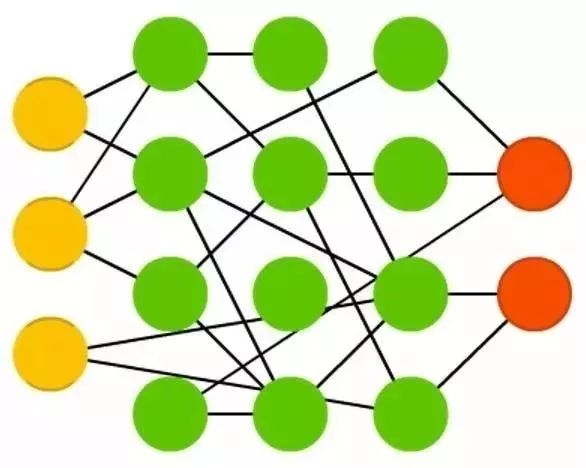
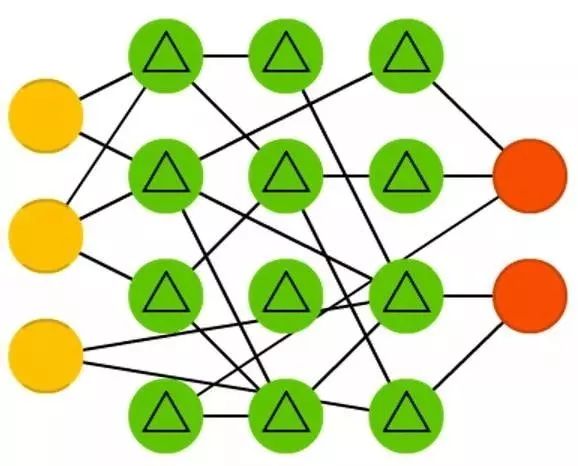
所以我决定写篇文章归纳归纳，各种神经网络结构。它们大部分都是神经网络，也有一些是完全不同的结构。虽然所有结构说起来都是新颖而独特的，但当我画出结点的结构图时……它们之间的内在联系显得更有意思。

总表

当我们在画节点图的时候发现了一个问题：这些图并没有展示出来这些神经结构是怎么使用的。

打个比方，变分自编码器（ VAE ）看起来跟自编码器（ AE ）真的差不多，但它们的训练过程却相差很远。在使用训练好的网络时更为不同，因为 VAE 是生成器，是通过添加噪音来获得新样本的。而 AE 只是简单地通过搜索记忆，找到与输入最接近的训练样本。

我需要强调的是，这个图并不能反映不同节点结构内部是如何运作的（这已经不是今天的话题了）。

需要注意的是，虽然我们使用的大部分简称是被普遍接受的，仍有一些并非如此。RNN 有的时候指的是递归神经网络（ recursive neural networks ），但大部分时候指的是循环神经网络（ recurrent neural networks ）。有时能看到 RNN 会被用来代表任何循环结构，包括 LSTM， GRU 甚至是双向网络的变型。 AE 偶尔也有类似的问题， VAE 和DAE 有时也被称为 AE 。许多简称在末尾的 N 的数量上有区别，因为你可以管卷积神经网络（ convolutional neural network ）叫成卷积网络（ convolutional network ）（就会形成两种简称： CNN 和 CN ）。

因为新的网络一直在不断地出现，构建一张完整的列表实际上是不可能的。就算是有这么一张表格，你在表格里找某一个也相当吃力，有时你会忽视掉一部分。所以虽然这张列表或许可以为你打开人工智能世界的大门， 但决不能认为这张表格列出了所有的结构，特别是当这篇文章写完很久之后，你才读到它。

对每个图片里的结构，我都写了一个非常非常简短的说明。如果你对某类结构很熟悉但对具体某个结构不熟的话，你可能会觉得这些说明挺有用的。

1

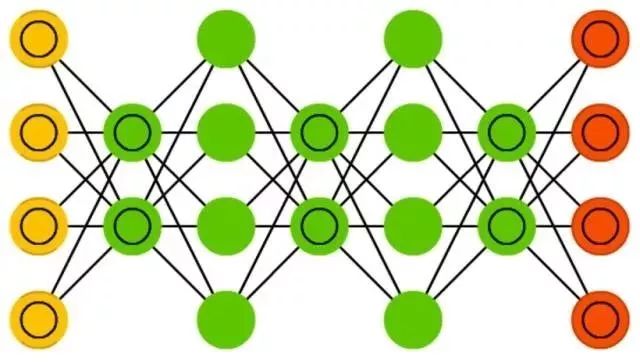
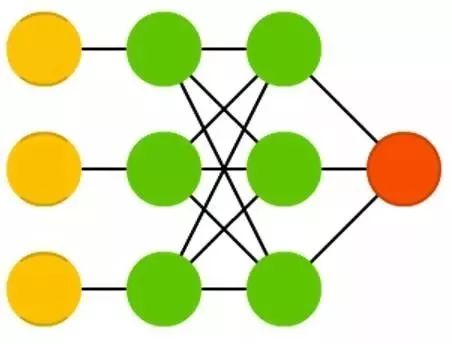
前馈神经网络（ FF 或 FFNN ）和感知机（ P ）十分直接，信息从前端一路传递到后端（从输入到输出）。神经网络通常有层的概念，每层可能是输入单元，隐藏单元或者输出单元组成。单个层内没有连接，通常是两个相邻的层之间全连接，（一层的所有神经元都和另一层的所有神经元互相连接）。

最简单但有效的神经网络有两个输入单元，一个输出单元，可以用于构建逻辑门。通常给网络的是成对的信息，输入和我们希望的输出，用反向传播来训练 FFNN 。这种叫做监督学习，和无监督学习相反，无监督学习是我们只给网络输入，让网络自己填补空缺。反向传播的误差通常是模型给定的输出和应该的输出之间的差距的某种变型（比如说 MSE 或者就是线性的做差）。如果网络有足够多的隐藏神经元，理论上它总可以给出输入和输出之间的关系建模。实际运用它们中有一定的局限性，但经常和其他网络组合起来构成新的网络。

Rosenblatt, Frank. “The perceptron: a probabilistic model for information storage and organization in the brain.” Psychological review 65.6 (1958): 386.

2

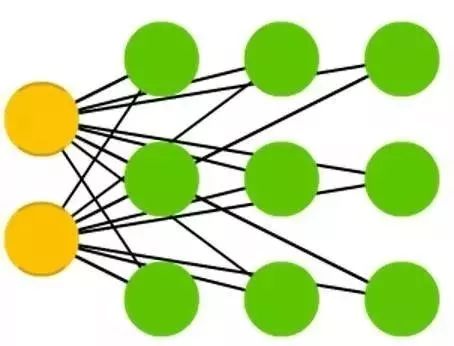
径向基函数（ RBF ）网络是 FFNN 网络附上径向基函数作为激活函数。就只是这样而已。我不是说它没什么用，而是大部分用其他激活函数的 FFNN 没有专用的名字。 这个有名字主要只是因为它恰巧在对的时间被发现了。

Broomhead, David S., and David Lowe. Radial basis functions, multi-variable functional interpolation and adaptive networks. No. RSRE-MEMO-4148. ROYAL SIGNALS AND RADAR ESTABLISHMENT MALVERN (UNITED KINGDOM), 1988.

3

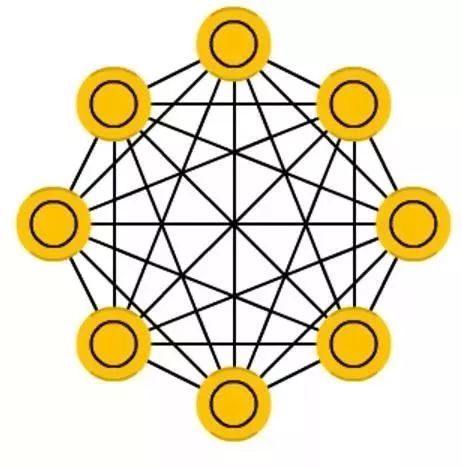
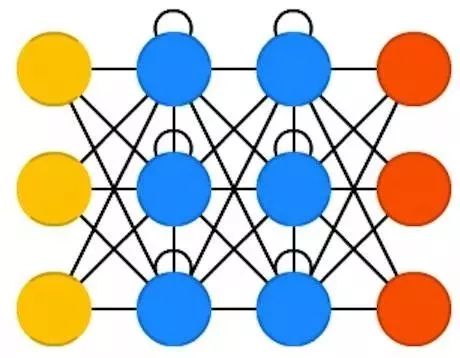
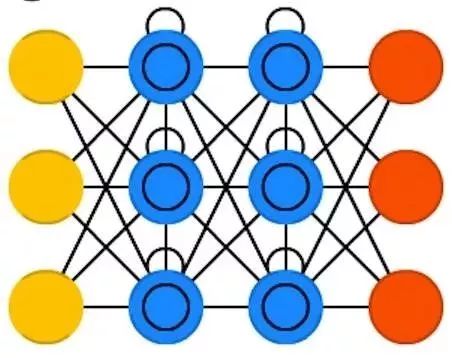
Hopfield 网络（ HN ）是一个每个神经元都和其他的神经元互相连接的网络； 它就是一盘彻底纠缠在一起的意大利面，每个节点也是如此。每个节点既是训练前的输入，又是训练中的隐藏节点，还是最后的输出。网络中的训练过程先计算出权重，然后每个神经元设置成我们想要的值。这个值将不再变动。一旦训练了一种或多种模式，网络最终会收敛到某个学习好的模式，因为网络只在这些状态上稳定。

请注意，网络不一定符合想要的结果。（可惜它并不是一个有魔法的黑箱子）它能够稳定部分源于网络的总能量或是随着训练逐渐降低的温度。每个神经元有一个对应于温度的激活阈值，如果输入的值加起来的和超过了这个阈值，神经元就会返回两个状态之一（通常是 -1 或 1 ，有时是 0 或 1 ）。网络的更新可以同步完成，更通常的做法是一个一个更新参数。如果一个一个更新的话，会产生一个公平随机的序列来决定单元更新的顺序（公平随机指的是一共 n 个选项一个个地更新，一共循环 n 次）。

所以你可以说当每个单元都更新过而且每个都不变了，这个网络稳定（退火）了（完成了收敛）。这个网络通常被称为联想记忆因为它能够收敛到和输入最相近的状态。如果人们能看到一半的桌子，我们能想出另一半桌子，同样地这个网络也会由残缺的半个桌子和一些噪音收敛到一个完整的桌子。

Hopfield, John J. “Neural networks and physical systems with emergent collective computational abilities.” Proceedings of the national academy of sciences 79.8 (1982): 2554-2558.

4

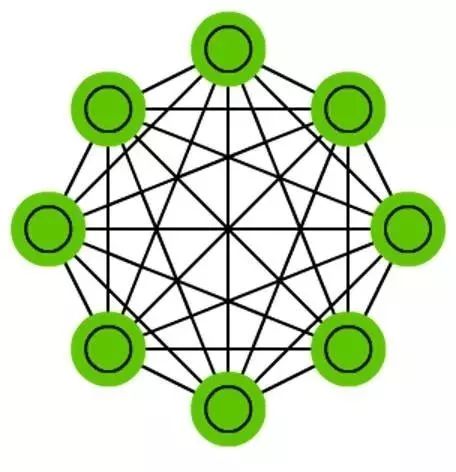
马尔可夫链（ MC 或离散时间马尔可夫链， DTMC ）是 BM 和 HN 的前身。它可以这样理解：从我在的节点，到达我周围的节点的概率是多少？它们是无记忆的（这就是马尔可夫性质），这意味着下一状态转移到哪里完全依赖于上一个状态。这不能算是一个神经网络，但是有一点类似神经网络，而且是 BM 和 HN 的理论基础。 MC 通常我们认为它不是一个神经网络， BM，RBM，HN 也是。马尔可夫链不一定是全连接的。

Hayes, Brian. “First links in the Markov chain.” American Scientist 101.2 (2013): 252.

5

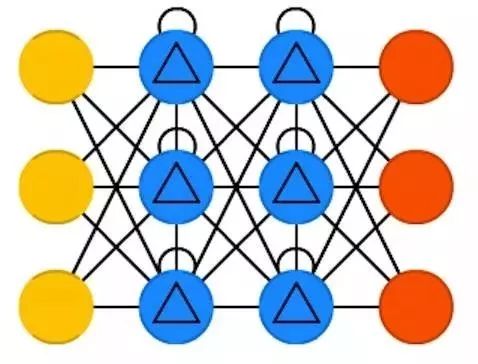
玻尔兹曼机（ BM ）和 HN 非常相似，但有些神经元被标注为输入神经元，其他的仍然是隐藏的。这些输入神经元在完成了整个网络更新后会成为输出神经元。它从随机权重开始通过反向传播学习，最近也会使用对比散度（一个用来决定两个信息增益之间梯度的马尔科夫链）学习。对比 HN， 神经元通常有二元激活模式。由于使用 MC 训练，BM 是一个随机网络。

BM 的训练和使用和 HN 很相似：把输入神经元设到箝位值然后这个网络就自由了（不用外力了）。这些单元在自由之后可以取任何值，我们在输入神经元和隐藏神经元间而反复迭代。激活模式是由全局温度控制的，更低的全局温度会降低单元的能量并令激活模式稳定下来。网络会在合适的温度下达到平衡点。

Hinton, Geoffrey E., and Terrence J. Sejnowski. “Learning and releaming in Boltzmann machines.” Parallel distributed processing: Explorations in the microstructure of cognition 1 (1986): 282-317.

6

限制玻尔兹曼机（ RBM ）和 BM 非常类似（惊不惊喜）所以也和 HN 类似。RBM 和 BM最大的区别是 RBM 更利于使用因为它是受限制的。它们不是每个神经元都和其他相连，而是每个组的神经元和别的组的神经元连接，所以没有输入神经元直接连接到其他输入神经元，也没有隐藏神经元连接到其他隐藏神经元。 RBM 可以类似于 FFNN 的训练方式来训练，但要做一点点改变：不是把信息从头传到末再反向传播误差，而是先把信息从头传到末，再把信息反向传回（到第一层）。然后接着开始用前向和反向传播来训练。

Smolensky, Paul. Information processing in dynamical systems: Foundations of harmony theory. No. CU-CS-321-86. COLORADO UNIV AT BOULDER DEPT OF COMPUTER SCIENCE, 1986.

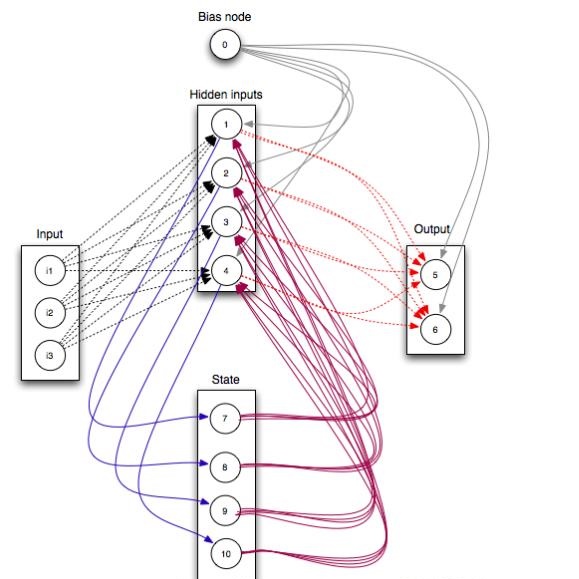
7

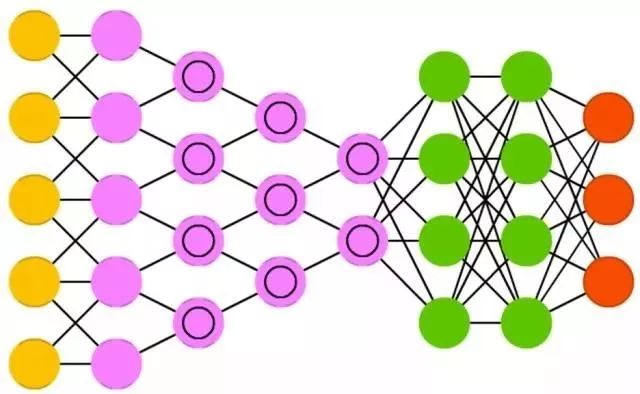
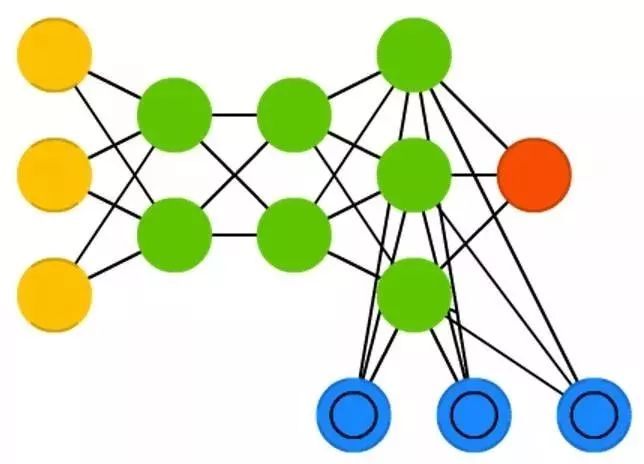
自编码（ AE ）有一点类似 FFNN， 因为 AE 更像是一个 FFNN 的别的用法而不是一个完全新的结构。自编码的基本思想是对信息自动地编码（像是压缩但不是加密），由此得名。整个网络的形状像一个沙漏，隐藏层比输入层和输出层都小。 AE 通常是关于中间层（一层或两层，因为层数可以是奇数或偶数）对称的。最小的一层通常在最中间，这里是信息最为压缩的地方（网络的阻塞点）。中间层的上方都称为编码区，下方都称为解码区，中间（意不意外）称为编码。我们可以给定输入，误差设置为输入和输出的差异，并用反向传播误差来训练网络。 AE 可以设计成对称的权重结构，这样编码权重和解码权重就一样了。

Bourlard, Hervé, and Yves Kamp. “Auto-association by multilayer perceptrons and singular value decomposition.” Biological cybernetics 59.4-5 (1988): 291-294.

8

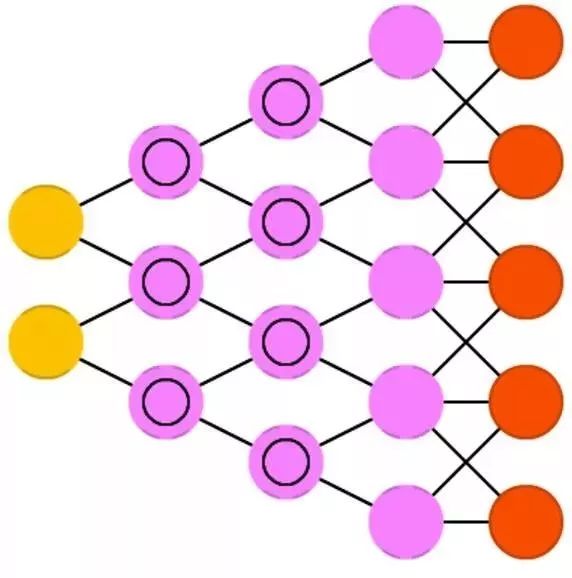
稀疏自编码（ SAE ）某种程度上是 AE 的反面。我们并不是教网络把一堆信息用更少的空间或者节点表示，而是试图把信息编码到更大的空间中。所以我们并不把网络在中间收缩，再放大到输入的规模，反而是把中间层的规模扩大。这种网络可以用来在数据集中提取许多小特征。

如果我们用训练 AE 的方式训练 SAE 的话，那大概率我们会得到一个完全没用的恒等网络 （进去什么样出来还是什么样，什么转换函数或者分解都没有）。为了防止这种情况发生，我们不反馈输入，而是反馈输入加稀疏驱动器。这个稀疏驱动器是一种阈值过滤器，只能让某个特定的误差回传参与到训练中，其他的误差都是无关的并被置为 0 。这样它就模拟了脉冲神经网络，不是所有的神经元都一起激活（具有生物合理性）。

Marc’Aurelio Ranzato, Christopher Poultney, Sumit Chopra, and Yann LeCun. “Efficient learning of sparse representations with an energy-based model.” Proceedings of NIPS. 2007.

9

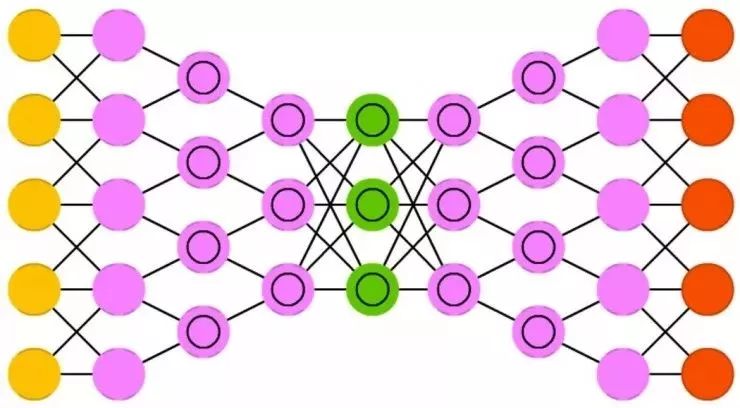
变分自编码器（ VAE ）和 AE 有一样的结构， 但被教授了一些别的东西：一个近似输入样本的概率分布。有一点不忘初心的意思，它和 BM 和 RBM 联系更紧密。但它总归还是基于贝叶斯模型作为概率推断和独立性，以及重新参数化的技巧来完成不一样的表征。概率推断和独立性的部分解释起来挺直观，但它们其实是基于复杂的数学。

这些基础可以这样理解：把影响考虑进来。如果一件事在某个地方发生了，另一件事在另一个地方发生，它们不一定相关的。如果它们不相关，那么误差传播应该考虑到这一点。这是一个很有用的方法因为神经网络（某种程度上来说）是一个很大的图模型，所以这个方法可以帮助我们排除某些节点对其他节点的影响，帮助我们深入更深的层。

Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).

10

去噪自编码器（ DAE ）是一个 AE ，但我们不只给它输入信息，而给它带有噪声的（比如把图片调成更有颗粒感）信息输入。我们有一样计算误差，但网络的输出和原有的不带噪声的输入进行比较。这样有利于网络不拘泥于学习细节，而是学习一些更广泛的特征，因为小的特征往往是错的，会随着噪音经常变动。

Vincent, Pascal, et al. “Extracting and composing robust features with denoising autoencoders.” Proceedings of the 25th international conference on Machine learning. ACM, 2008.

11

深度信念网络（ DBN ）是一个堆叠的结构，往往是 RBM 或是 VAE 堆叠起来的。这个网络被证实能够逐层地有效地训练，每个 AE 或 RBM 只要学会对前一层的网络进行编码。这个技巧也称为贪心训练，贪心意味着对于局部最优解决方案找到了一个不错的解但不一定是最优解。 DBN 可以通过对比散度或是反向传播来训练，学习用概率模型的方式表征数据，就像普通的 RBM 或是 VAE 。一旦非监督学习训练或者收敛到一个比较稳定的状态，这个模型可以用来生成新的数据。如果是使用对比散度来训练的，那这个网络甚至还可以用来对已有的数据进行分类，因为神经元被训练于寻找不同的数据特征。

Bengio, Yoshua, et al. “Greedy layer-wise training of deep networks.” Advances in neural information processing systems 19 (2007): 153.

12

卷积神经网络（ CNN 或深度卷及神经网络 DCNN ）和其他大部分网络很不一样。它们最初是用来处理图像的，但现在也被用来处理其他形式的输入比如说音频。

CNN 的一种典型的用途是给网络输入图片，让网络来分类这些数据，比如说当我们给它一张猫的图片，网络输出 “猫”；当我们给出一张狗的图片，网络输出“狗”。 CNN 通常由一个输入“扫描仪”开始，而不是一次性分析全部的输入。打个比方，我们输入一张 200 x 200 像素的图片，我们并不想要一层 40000 个节点的一层，相反，我们创建一个 20 x 20 的输入扫描仪层，就是说从一开始的 20 x 20 个像素点进行输入（通常是图片的左上角）。

当我们把这个输入完成后（有可能是用于训练），我们输入下一个 20 x 20 个像素：我们把这个扫描仪往右平移一个像素。注意到我们并不把一下子平移 20 个像素（或者扫描仪的宽度），我们并不把图片拆解成 20 x 20 的块，而是一点点地爬过去。输入数据被送入卷积层，而不是普通的层，卷积层里面的节点不是和其他所有节点相连接的。

每个节点只关注与自身和周边的节点（多近的周边取决于具体实现，但通常不会很多）。卷积层往往会随着层次更深而收缩，大部分是按照可以整除输入层大小的倍数收缩（比如说 20 后面的层可能是 10 接下来是 5）。2 的幂次更为常用，因为它们可以被整除干净：32，16，8，4，2，1。除开卷积层，网络里常常还有池化层。池化是一种过滤掉细节的方法：一种常见的池化技巧是最大池化，比如我们取 2 x 2 的像素，传递出的是红色值最大的像素点。

把 CNN 用在音频上，我们通常输入音频波形，一片段一片段地缓慢移动音频片段。CNN 的实际实现往往在网络末端加上一个 FFNN 用于进一步处理信息，这样可以加入一些高度非线性的抽象。这种网络被称为 DCNN ，但这两个名字和简称往往可以混用。

LeCun, Yann, et al. “Gradient-based learning applied to document recognition.” Proceedings of the IEEE 86.11 (1998): 2278-2324.

新的神经网络结构不断涌现，我们很难一一掌握。哪怕一开始只是记住所有的简称（ DCIGN，BiLSTM，DCGAN ），也会让同学们吃不消。

所以我决定写篇文章归纳归纳，各种神经网络结构。它们大部分都是神经网络，也有一些是完全不同的结构。虽然所有结构说起来都是新颖而独特的，但当我画出结点的结构图时……它们之间的内在联系显得更有意思。

13

反卷积网络（DN）又名逆向图网络（IGN），是卷积神经网络的逆转。举个栗子：输入“猫”这个词，通过对比网络生成的图像和猫的真实图像来训练网络，使网络产生更像猫的图像。DN 可以像常规 CNN 那样与 FFNN 相结合，这样就需要给它一个新的“缩写”了。“深度反卷积网络”的称呼大概可行，但你可能会反驳说，分别把 FFNN 接在 DN 的前端或后端时，应该用两个不同的名字来指代。

在大多数应用场合，输入网络的不是文字式的类别信息而是二值向量。 如 <0，1> 表示猫，<1，0> 表示狗，<1，1> 表示猫和狗。在 DN 中，CNN常见的采样层被类似的反向操作替换，主要有插值方法和带有偏置假设的外推方法等等（如果采样层使用最大值采样，可以在做逆向操作时单独制造出一些比最大值小的新数据。）

Zeiler, Matthew D., et al. “Deconvolutional networks.” Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010.

14

深度卷积逆向图网络（DCIGN）的名称有一定的误导性，它实际上是一类变分自动编码器（VAE），只不过分别用 CNN 作编码器、DN 作解码器了。DCIGN 在编码时试图将“特征”以概率建模，这样一来就算仅仅学习了只有猫或狗一方存在的图像，它也能够学着去产生猫狗共存的图片。假如一张照片里既有猫，又有邻居家那条讨厌的狗，你可以把照片输入网络，让网络自动把那条狗扒出去，而无须额外的操作。演示程序表明，该网络还能学习对图像做复杂的变换，比如改变光源和旋转3D物体。该网络通常使用反向传播来训练。

Kulkarni, Tejas D., et al. “Deep convolutional inverse graphics network.” Advances in Neural Information Processing Systems. 2015.

15

生成对抗网络（GAN）源出另一类网络，它由两个成对的网络协同运作。GAN 由任意两个的网络组成（不过通常是 FFNN 和 CNN 的组合），一个用来生成，另一个用来判别。判别网络的输入是训练数据或者生成网络产生的内容，它正确区分数据来源的能力构成了生成网络错误水平的表现的一部分。这样就形成了一种竞争形式：判别器越来越擅长区分真实数据和生成数据，与此同时生成器不断学习从而让判别器更难区分。有时候，这样的机制效果还不错，因为即便是相当复杂的类噪声模式最终都是可预测的，但与输入数据特征相似的生成数据更难区分。GAN 很难训练——你不仅需要训练两个网络（它们可能都有自己的问题），还要很好地平衡它们的动态情况。如果预测或者生成任意一方比另一方更强，这个 GAN 就不会收敛，而是直接发散掉了。

Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in Neural Information Processing Systems. 2014.

16

循环神经网络（RNN）是带有“时间结”的 FFNN。RNN 不是无状态的[1]，它既存在层间的联系，也存在时间上的联系。输入到神经元的信息不仅由上一层传来，还来自前次传递时神经元自身的状态。这意味着输入和训练网络的顺序很关键：先输入“牛奶”、再输入“曲奇”，与先输入“曲奇”再输入“牛奶”会得到不同的结果。RNN 的一大问题是，使用不同的激励函数会各自造成梯度弥散或者爆炸，这样会让信息随时间变化而迅速流失，就像在极深 FFNN 中随深度增加而流失一样。乍一看好像不是什么大问题，因为这些信息只是权重而不是神经元的状态。

但是，不同时间上的权值实际存储了来自过去的信息，而如果权值变成了 0 或 100 0000，就无所谓之前的状态了。大体上说，RNN 可以用在很多领域。尽管大部分数据并不存在形如音频、视频之类的时间线，但不妨把它们表示为序列的形式。图像、文字序列可以用每次一个像素、字符的方式来输入，这样，时间相关的权值并非来自前 x 秒出现的状态，而是对序列早前状态的表示。通常来说，循环网络善于预测和补全信息，比如可以用来做自动的补全。

[1] “无状态的（stateless）”，意为“输出仅由本时刻的输入决定”。RNN 由于部分“记忆”了之前输入的状态，所以是“有状态的（stateful）”。——译注。

Elman, Jeffrey L. “Finding structure in time.” Cognitive science 14.2 (1990): 179-211.

17

长短时记忆（LSTM）网络试图通过引进“门”和定义明确的记忆单元来对抗梯度弥散/爆炸问题。相较生物学，它更多受到电路学的启发。每个神经元有一个记忆单元和输入、输出、遗忘三个门。门的作用是通过阻止和允许信息的流动来实现对信息的保护。输入门决定了前一层的信息有多少能够存储在当前单元内；另一端的输出门决定了后一层能够在当前单元中获取多少信息；遗忘门乍看起来有点奇怪，但“遗忘”有时候是对的——比如正在学习一本书，然后新的一章开始了，这时候网络可能得忘掉一些在上一章中学到的文字。LSTM 能够学习复杂的序列，可以像莎士比亚一样写作、创作新的乐曲。由于每个门对都有对前一个神经元的权重，网络运行需要更多的资源。

Hochreiter, Sepp, and Jürgen Schmidhuber. “Long short-term memory.” Neural computation 9.8 (1997): 1735-1780.

18

门控循环单元（GRU）由LSTM的稍作变化而来。GRU 减少了一个门，还改变了连接方式：更新门取代了输入、输出、遗忘门。更新门决定了分别从上一个状态和前一层网络中分别保留、流入多少信息；重置门很像 LSTM 的遗忘门，不过位置稍有改变。GRU 会直接传出全部状态，而不是额外通过一个输出门。通常，GRU 与 LSTM 功能接近，最大的区别在于， GRU 速度更快、运行也更容易（不过表达能力稍弱）。实践中运行性能可能与表达能力相互抵消：运行一个更大的网络来获得更强的表达能力时，运行性能的优势会被压制。而在不需要额外的表达能力时，GRU 的性能超过 LSTM。

Chung, Junyoung, et al. “Empirical evaluation of gated recurrent neural networks on sequence modeling.” arXiv preprint arXiv:1412.3555 (2014).

19

神经图灵机（NTM）可以理解为 LSTM 的抽象形式。它试图将神经网络“去黑盒化”，从而让我们部分了解神经网络内部发生了什么。不同于直接把记忆单元编码进神经元，NTM 的记忆被分开了。NTM 想把常规数字化存储的高效性与持久性、神经网络的高效性与表达能力结合起来；它的设想是，建立内容可寻址的记忆组，以及可读写这个记忆组的神经网络。“神经图灵机”中的“图灵”是说它是图灵完备的：能够读、写，以及根据读入内容改变状态。这就是说，它可以表达通用图灵机所能表达的一切。

Graves, Alex, Greg Wayne, and Ivo Danihelka. “Neural turing machines.” arXiv preprint arXiv:1410.5401 (2014).

20

双向循环网络，双向长短时记忆网络和双向门控循环单元（BiRNN，BiLSTM 和 BiGRU）同它们的单向形式看上去完全一样，所以不画出来了。区别在于，这些网络不仅与过去的状态连接，还与未来的状态连接。举例来说，让单向 LSTM 通过依次输入字母的形式训练，来预测单词 “fish”，此时时间轴上的循环连接就记住了之前状态的值。而双向 LSTM 在反向传值的时候会继续得到序列接下来的字母，即获得了未来的信息。这就教会了网络填补空隙、而不是预测信息——它们不是去扩展图像的边缘，而是填充图像的中空。

Schuster, Mike, and Kuldip K. Paliwal. “Bidirectional recurrent neural networks.” IEEE Transactions on Signal Processing 45.11 (1997): 2673-2681.

21

深度残差网络（DRN）是在逐层连接的基础上，带有额外层间连接（通常间隔二到五层）的极深 FFNN。DRN 不像常规网络那样，力求解得输入到输出经过多层网络传递后的映射关系；它往解中添加了一点儿恒等性，即把浅层的输入直接提供给了更深层的单元。实验证明，DRN 可以高效地学得深达150层的网络，其性能远远超过了常规的二到五层的简单网络。然而有人证明，DRN 其实是不具备明确时间结构的 RNN，所以经常被类比作没有门单元的 LSTM。

He, Kaiming, et al. “Deep residual learning for image recognition.” arXiv preprint arXiv:1512.03385 (2015).

22

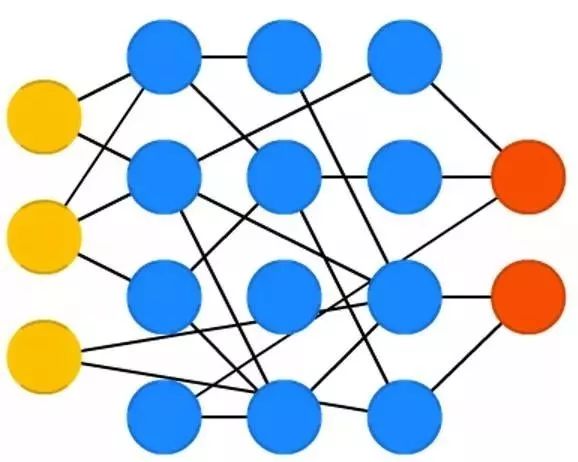
回声状态网络（ESN）是另一种循环网络。与一般网络的不同在于，ESN 神经元之间的连接是随机的（就是说，没有整齐的层-层形式），训练过程自然也就不同。数据前向输入、误差反向传播的法子不能用了，我们需要把数据前向输入，等一会儿再更新单元，再等一会儿，最后观察输出。与一般神经网络相比，ESN 中输入和输出层的角色发生了相当的改变——输入层把信息填充给网络、输出层观察激活模式随时间展开的状态。训练时，只有输出层和一部分隐层单元之间的连接会被改变。

Jaeger, Herbert, and Harald Haas. “Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication.” science 304.5667 (2004): 78-80.

23

极限学习机（ELM）基本上是随机连接的 FFNN。看上去很像 LSM 和 ESN，但 ELM 既不是循环式的、也不是脉冲式的。ELM 也不用反向传播，而是初始化为随机权值，然后用最小二乘拟合（在所有函数上误差最小）、一步到位地完成训练。这样得到的是一个表达能力稍弱，但远快于使用反向传播的神经网络。

Cambria, Erik, et al. “Extreme learning machines [trends & controversies].” IEEE Intelligent Systems 28.6 (2013): 30-59.

24

液体状态机（LSM）跟 ESN 比较像，区别在于 LSM 是一类脉冲神经网络： sigmoid 激活函数被阈值函数取代；每个神经元都是累加的记忆单元。所以更新神经元时，它的值不是相连神经元的和，而是自身的累加，一旦达到阈值就把能量释放给其他神经元。这就形成了脉冲式的网络——超过阈值后，状态才会改变。

Maass, Wolfgang, Thomas Natschläger, and Henry Markram. “Real-time computing without stable states: A new framework for neural computation based on perturbations.” Neural computation 14.11 (2002): 2531-2560.

25

支持向量机（SVM）为分类问题找到最优解。最初 SVM 只能处理线性可分的数据，比如判断哪张是加菲猫，哪张是史努比，而不存在其他的情况。可以这样理解 SVM 的训练：将所有的数据（比如加菲猫和史努比）在（2D）图上画出，在两类数据中间想办法画一条线，这条线把数据区分开，即所有的史努比在这边、所有的加菲猫在另一边。通过最大化两边数据点与这条分割线的间隔来找到最优解。对新的数据做分类时，只要把数据点画在图上，看看它在线的那一边就好了。使用核方法可以分类 n 维数据，这时需要把点画在三维图中，从而让 SVM 能够区分史努比、加菲猫和——比如说西蒙的猫——或者是更高的维度、更多的卡通形象类别。有时候，人们也不把 SVM 当成神经网络。

Cortes, Corinna, and Vladimir Vapnik. “Support-vector networks.” Machine learning 20.3 (1995): 273-297.

26

最后介绍 Kohonen 网络（KN，也叫自组织（特征）图，SOM，SOFM）。KN 利用竞争性学习来无监督地分类数据。输入数据之后，网络会评估哪些神经元与输入的匹配度最高，然后做微调来继续提高匹配度，并慢慢带动邻近它们的其他神经元发生变化。邻近神经元被改变的程度，由其到匹配度最高的单元之间的距离来决定。Kohonen有时候也不被认为是神经网络。

媒体合作请联系：

邮箱：contact@dataunion.org