干货 | 史上最好记的神经网络结构速记表（下）

原文THE NEURAL NETWORK ZOO，出自Asimov人工智能研究所。

翻译 / 唐青

校对 / 李宇琛

整理 / 雷锋字幕组

本文提供了神经网络结构速查表，全面盘点神经网络的大量框架，并绘制直观示意图进行说明，是人手必备的神经网络学习小抄。昨天，我们发布了 史上最好记的神经网络结构速记表（上） ，今天继续来看其余的14种神经网络结构。

新的神经网络结构不断涌现，我们很难一一掌握。哪怕一开始只是记住所有的简称（ DCIGN，BiLSTM，DCGAN ），也会让同学们吃不消。

所以我决定写篇文章归纳归纳，各种神经网络结构。它们大部分都是神经网络，也有一些是完全不同的结构。虽然所有结构说起来都是新颖而独特的，但当我画出结点的结构图时……它们之间的内在联系显得更有意思。

总  表

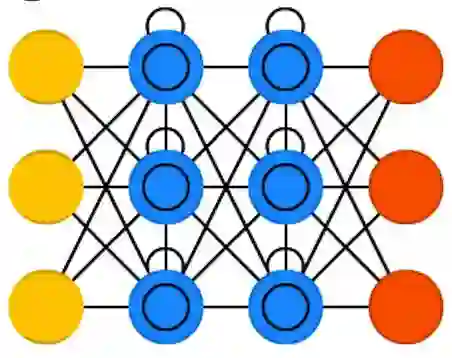
13、反卷积网络（DN）

反卷积网络（DN）又名逆向图网络（IGN），是卷积神经网络的逆转。举个栗子：输入“猫”这个词，通过对比网络生成的图像和猫的真实图像来训练网络，使网络产生更像猫的图像。DN 可以像常规 CNN 那样与 FFNN 相结合，这样就需要给它一个新的“缩写”了。“深度反卷积网络”的称呼大概可行，但你可能会反驳说，分别把 FFNN 接在 DN 的前端或后端时，应该用两个不同的名字来指代。

在大多数应用场合，输入网络的不是文字式的类别信息而是二值向量。 如 <0，1> 表示猫，<1，0> 表示狗，<1，1> 表示猫和狗。在 DN 中，CNN常见的采样层被类似的反向操作替换，主要有插值方法和带有偏置假设的外推方法等等（如果采样层使用最大值采样，可以在做逆向操作时单独制造出一些比最大值小的新数据。

Zeiler, Matthew D., et al. “Deconvolutional networks.” Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010.

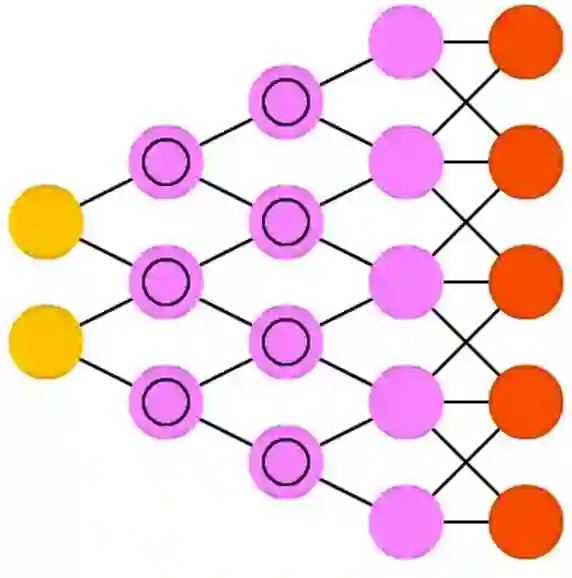
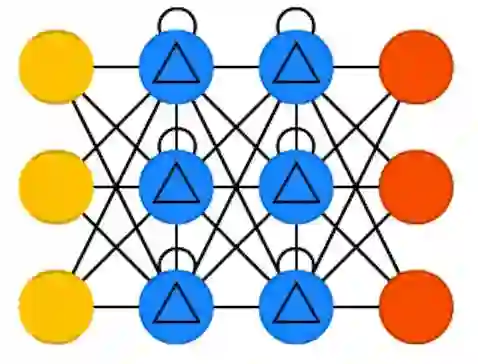
14、深度卷积逆向图网络（DCIGN）

深度卷积逆向图网络（DCIGN）的名称有一定的误导性，它实际上是一类变分自动编码器（VAE），只不过分别用 CNN 作编码器、DN 作解码器了。DCIGN 在编码时试图将“特征”以概率建模，这样一来就算仅仅学习了只有猫或狗一方存在的图像，它也能够学着去产生猫狗共存的图片。假如一张照片里既有猫，又有邻居家那条讨厌的狗，你可以把照片输入网络，让网络自动把那条狗扒出去，而无须额外的操作。演示程序表明，该网络还能学习对图像做复杂的变换，比如改变光源和旋转3D物体。该网络通常使用反向传播来训练。

Kulkarni, Tejas D., et al. “Deep convolutional inverse graphics network.” Advances in Neural Information Processing Systems. 2015.

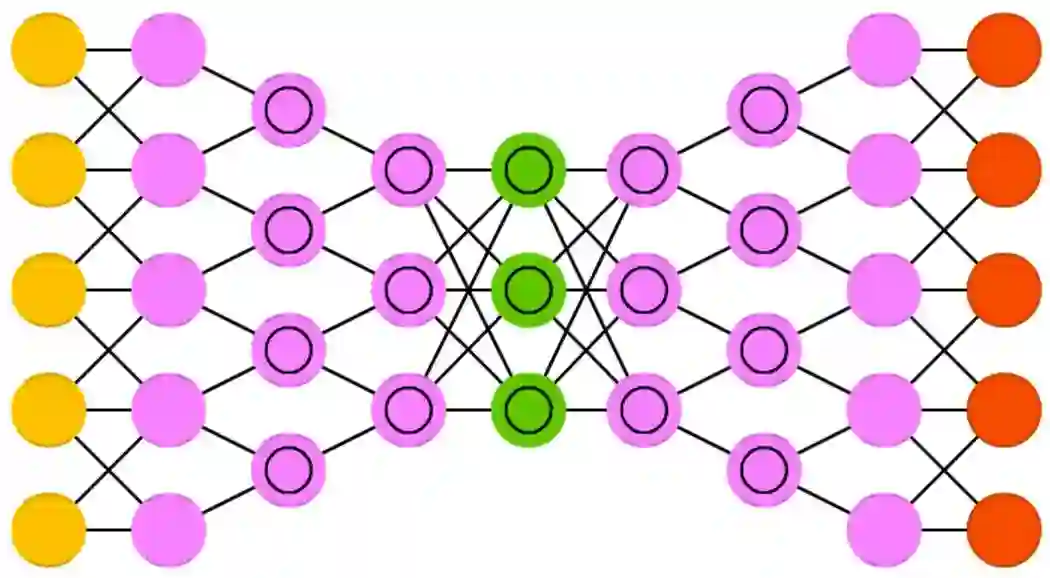
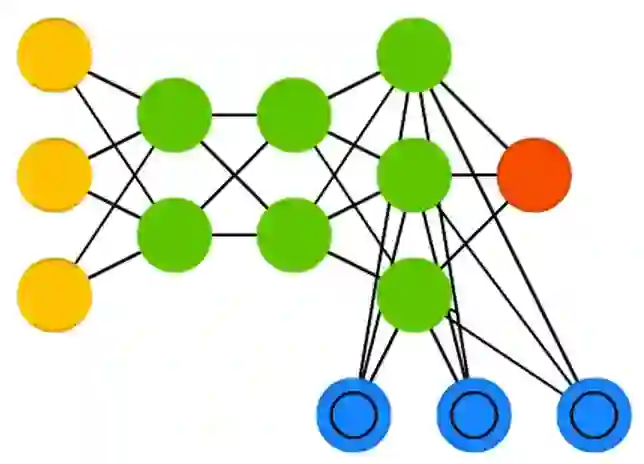
15、生成对抗网络（GAN）

生成对抗网络（GAN）源出另一类网络，它由两个成对的网络协同运作。GAN 由任意两个的网络组成（不过通常是 FFNN 和 CNN 的组合），一个用来生成，另一个用来判别。判别网络的输入是训练数据或者生成网络产生的内容，它正确区分数据来源的能力构成了生成网络错误水平的表现的一部分。这样就形成了一种竞争形式：判别器越来越擅长区分真实数据和生成数据，与此同时生成器不断学习从而让判别器更难区分。有时候，这样的机制效果还不错，因为即便是相当复杂的类噪声模式最终都是可预测的，但与输入数据特征相似的生成数据更难区分。GAN 很难训练——你不仅需要训练两个网络（它们可能都有自己的问题），还要很好地平衡它们的动态情况。如果预测或者生成任意一方比另一方更强，这个 GAN 就不会收敛，而是直接发散掉了。

Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in Neural Information Processing Systems. 2014.

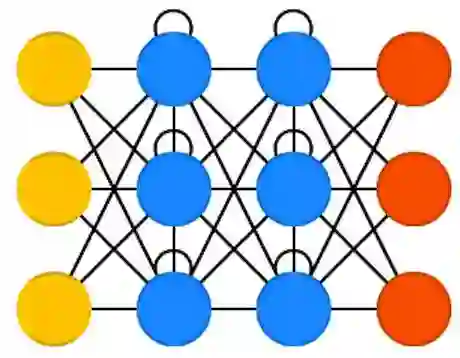
16、循环神经网络（RNN）

循环神经网络（RNN）是带有“时间结”的 FFNN。RNN 不是无状态的[1]，它既存在层间的联系，也存在时间上的联系。输入到神经元的信息不仅由上一层传来，还来自前次传递时神经元自身的状态。这意味着输入和训练网络的顺序很关键：先输入“牛奶”、再输入“曲奇”，与先输入“曲奇”再输入“牛奶”会得到不同的结果。RNN 的一大问题是，使用不同的激励函数会各自造成梯度弥散或者爆炸，这样会让信息随时间变化而迅速流失，就像在极深 FFNN 中随深度增加而流失一样。乍一看好像不是什么大问题，因为这些信息只是权重而不是神经元的状态。

但是，不同时间上的权值实际存储了来自过去的信息，而如果权值变成了 0 或 100 0000，就无所谓之前的状态了。大体上说，RNN 可以用在很多领域。尽管大部分数据并不存在形如音频、视频之类的时间线，但不妨把它们表示为序列的形式。图像、文字序列可以用每次一个像素、字符的方式来输入，这样，时间相关的权值并非来自前 x 秒出现的状态，而是对序列早前状态的表示。通常来说，循环网络善于预测和补全信息，比如可以用来做自动的补全。

[1] “无状态的（stateless）”，意为“输出仅由本时刻的输入决定”。RNN 由于部分“记忆”了之前输入的状态，所以是“有状态的（stateful）”。——译注。

Elman, Jeffrey L. “Finding structure in time.” Cognitive science 14.2 (1990): 179-211.

17、长短时记忆（LSTM）

长短时记忆（LSTM）网络试图通过引进“门”和定义明确的记忆单元来对抗梯度弥散/爆炸问题。相较生物学，它更多受到电路学的启发。每个神经元有一个记忆单元和输入、输出、遗忘三个门。门的作用是通过阻止和允许信息的流动来实现对信息的保护。输入门决定了前一层的信息有多少能够存储在当前单元内；另一端的输出门决定了后一层能够在当前单元中获取多少信息；遗忘门乍看起来有点奇怪，但“遗忘”有时候是对的——比如正在学习一本书，然后新的一章开始了，这时候网络可能得忘掉一些在上一章中学到的文字。LSTM 能够学习复杂的序列，可以像莎士比亚一样写作、创作新的乐曲。由于每个门对都有对前一个神经元的权重，网络运行需要更多的资源。

Hochreiter, Sepp, and Jürgen Schmidhuber. “Long short-term memory.” Neural computation 9.8 (1997): 1735-1780.

18、门控循环单元（GRU）

门控循环单元（GRU）由LSTM的稍作变化而来。GRU 减少了一个门，还改变了连接方式：更新门取代了输入、输出、遗忘门。更新门决定了分别从上一个状态和前一层网络中分别保留、流入多少信息；重置门很像 LSTM 的遗忘门，不过位置稍有改变。GRU 会直接传出全部状态，而不是额外通过一个输出门。通常，GRU 与 LSTM 功能接近，最大的区别在于， GRU 速度更快、运行也更容易（不过表达能力稍弱）。实践中运行性能可能与表达能力相互抵消：运行一个更大的网络来获得更强的表达能力时，运行性能的优势会被压制。而在不需要额外的表达能力时，GRU 的性能超过 LSTM。

Chung, Junyoung, et al. “Empirical evaluation of gated recurrent neural networks on sequence modeling.” arXiv preprint arXiv:1412.3555 (2014).

19、神经图灵机（NTM）

神经图灵机（NTM）可以理解为 LSTM 的抽象形式。它试图将神经网络“去黑盒化”，从而让我们部分了解神经网络内部发生了什么。不同于直接把记忆单元编码进神经元，NTM 的记忆被分开了。NTM 想把常规数字化存储的高效性与持久性、神经网络的高效性与表达能力结合起来；它的设想是，建立内容可寻址的记忆组，以及可读写这个记忆组的神经网络。“神经图灵机”中的“图灵”是说它是图灵完备的：能够读、写，以及根据读入内容改变状态。这就是说，它可以表达通用图灵机所能表达的一切。

Graves, Alex, Greg Wayne, and Ivo Danihelka. “Neural turing machines.” arXiv preprint arXiv:1410.5401 (2014).

20、双向循环网络

双向循环网络，双向长短时记忆网络和双向门控循环单元（BiRNN，BiLSTM 和 BiGRU）同它们的单向形式看上去完全一样，所以不画出来了。区别在于，这些网络不仅与过去的状态连接，还与未来的状态连接。举例来说，让单向 LSTM 通过依次输入字母的形式训练，来预测单词 “fish”，此时时间轴上的循环连接就记住了之前状态的值。而双向 LSTM 在反向传值的时候会继续得到序列接下来的字母，即获得了未来的信息。这就教会了网络填补空隙、而不是预测信息——它们不是去扩展图像的边缘，而是填充图像的中空

Schuster, Mike, and Kuldip K. Paliwal. “Bidirectional recurrent neural networks.” IEEE Transactions on Signal Processing 45.11 (1997): 2673-2681.

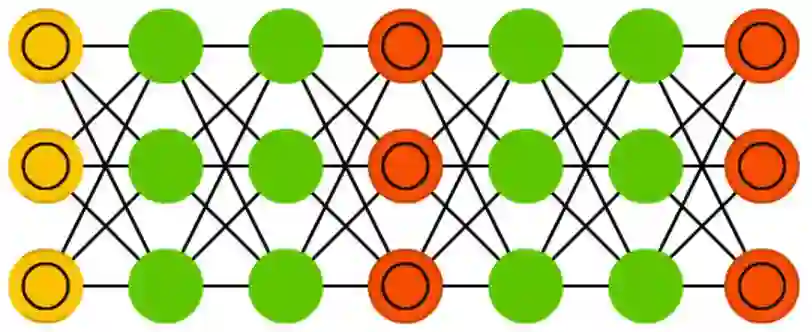
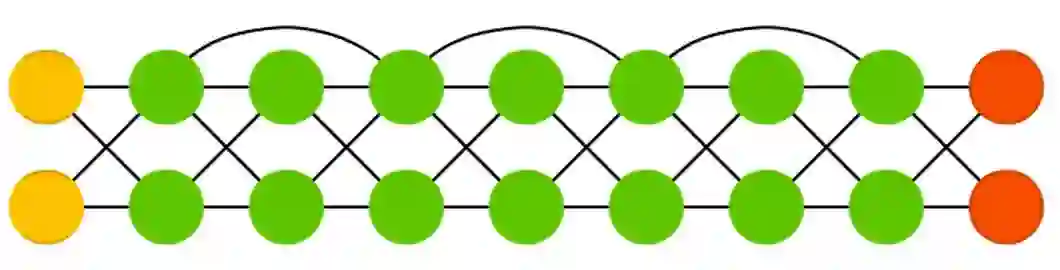
21、深度残差网络（DRN）

深度残差网络（DRN）是在逐层连接的基础上，带有额外层间连接（通常间隔二到五层）的极深 FFNN。DRN 不像常规网络那样，力求解得输入到输出经过多层网络传递后的映射关系；它往解中添加了一点儿恒等性，即把浅层的输入直接提供给了更深层的单元。实验证明，DRN 可以高效地学得深达150层的网络，其性能远远超过了常规的二到五层的简单网络。然而有人证明，DRN 其实是不具备明确时间结构的 RNN，所以经常被类比作没有门单元的 LSTM。

He, Kaiming, et al. “Deep residual learning for image recognition.” arXiv preprint arXiv:1512.03385 (2015).

22、回声状态网络（ESN）

回声状态网络（ESN）是另一种循环网络。与一般网络的不同在于，ESN 神经元之间的连接是随机的（就是说，没有整齐的层-层形式），训练过程自然也就不同。数据前向输入、误差反向传播的法子不能用了，我们需要把数据前向输入，等一会儿再更新单元，再等一会儿，最后观察输出。与一般神经网络相比，ESN 中输入和输出层的角色发生了相当的改变——输入层把信息填充给网络、输出层观察激活模式随时间展开的状态。训练时，只有输出层和一部分隐层单元之间的连接会被改变。

Jaeger, Herbert, and Harald Haas. “Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication.” science 304.5667 (2004): 78-80.

23、极限学习机（ELM）

极限学习机（ELM）基本上是随机连接的 FFNN。看上去很像 LSM 和 ESN，但 ELM 既不是循环式的、也不是脉冲式的。ELM 也不用反向传播，而是初始化为随机权值，然后用最小二乘拟合（在所有函数上误差最小）、一步到位地完成训练。这样得到的是一个表达能力稍弱，但远快于使用反向传播的神经网络。

Cambria, Erik, et al. “Extreme learning machines [trends & controversies].” IEEE Intelligent Systems 28.6 (2013): 30-59.

24、液体状态机（LSM）

液体状态机（LSM）跟 ESN 比较像，区别在于 LSM 是一类脉冲神经网络： sigmoid 激活函数被阈值函数取代；每个神经元都是累加的记忆单元。所以更新神经元时，它的值不是相连神经元的和，而是自身的累加，一旦达到阈值就把能量释放给其他神经元。这就形成了脉冲式的网络——超过阈值后，状态才会改变。

Maass, Wolfgang, Thomas Natschläger, and Henry Markram. “Real-time computing without stable states: A new framework for neural computation based on perturbations.” Neural computation 14.11 (2002): 2531-2560.

25、支持向量机（SVM）

支持向量机（SVM）为分类问题找到最优解。最初 SVM 只能处理线性可分的数据，比如判断哪张是加菲猫，哪张是史努比，而不存在其他的情况。可以这样理解 SVM 的训练：将所有的数据（比如加菲猫和史努比）在（2D）图上画出，在两类数据中间想办法画一条线，这条线把数据区分开，即所有的史努比在这边、所有的加菲猫在另一边。通过最大化两边数据点与这条分割线的间隔来找到最优解。对新的数据做分类时，只要把数据点画在图上，看看它在线的那一边就好了。使用核方法可以分类 n 维数据，这时需要把点画在三维图中，从而让 SVM 能够区分史努比、加菲猫和——比如说西蒙的猫——或者是更高的维度、更多的卡通形象类别。有时候，人们也不把 SVM 当成神经网络。

Cortes, Corinna, and Vladimir Vapnik. “Support-vector networks.” Machine learning 20.3 (1995): 273-297.

26、Kohonen 网络

最后介绍 Kohonen 网络（KN，也叫自组织（特征）图，SOM，SOFM）。KN 利用竞争性学习来无监督地分类数据。输入数据之后，网络会评估哪些神经元与输入的匹配度最高，然后做微调来继续提高匹配度，并慢慢带动邻近它们的其他神经元发生变化。邻近神经元被改变的程度，由其到匹配度最高的单元之间的距离来决定。Kohonen有时候也不被认为是神经网络。

Kohonen, Teuvo. “Self-organized formation of topologically correct feature maps.” Biological cybernetics 43.1 (1982): 59-69.

————————————————————