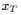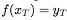DeepMind提出深度学习新方向:神经过程模型
来源:DeepMind 编译:肖琴,金磊
函数逼近是机器学习中许多问题的核心,DeepMind的最新研究结合了神经网络和随机过程的优点,提出神经过程模型,在多任务上实现了很好的性能和高计算效率。
论文:https://arxiv.org/pdf/1807.01622.pdf
函数逼近(Function approximation)是机器学习中许多问题的核心,在过去十年来,这个问题的一种非常流行的方法是深度神经网络。高级神经网络由黑盒函数逼近器构成,它们学习从大量训练数据点参数化单个函数。因此,网络的大部分工作负载都落在训练阶段,而评估和测试阶段则被简化为快速的前向传播。虽然高的测试时间性能对于许多实际应用是有价值的,但是在训练之后就无法更新网络的输出,这可能是我们不希望的。例如,元学习(Meta-learning)是一个越来越受欢迎的研究领域,解决的正是这种局限性。
作为神经网络的一种替代方案,还可以对随机过程进行推理以执行函数回归。这种方法最常见的实例是高斯过程( Gaussian process, GP),这是一种具有互补性质的神经网络模型:GP不需要昂贵的训练阶段,可以根据某些观察结果对潜在的ground truth函数进行推断,这使得它们在测试时非常灵活。
此外,GP在未观察到的位置表示无限多不同的函数,因此,在给定一些观察结果的基础上,它能捕获其预测的不确定性。但是,GP在计算上是昂贵的:原始GP对数据点数量是3次方量级的scale,而当前最优的逼近方法是二次逼近。此外,可用的kernel通常以其函数形式受到限制,需要一个额外的优化过程来为任何给定的任务确定最合适的kernel及其超参数。
因此,将神经网络和随机过程推理结合起来,弥补两种方法分别具有的一些缺点,这作为一种潜在解决方案越来越受到关注。在这项工作中,DeepMind研究科学家Marta Garnelo等人的团队提出一种基于神经网络并学习随机过程逼近的方法,他们称之为神经过程(Neural Processes, NPs)。NP具有GP的一些基本属性,即它们学习在函数之上建模分布,能够根据上下文的观察估计其预测的不确定性,并将一些工作从训练转移到测试时间,以实现模型的灵活性。
更重要的是,NP以一种计算效率非常高的方式生成预测。给定n个上下文点和m个目标点,一个经过训练的NP的推理对应于一个深度神经网络的前向传递,它以
scale,而不是像经典GP那样以
。此外,该模型通过直接从数据中学习隐式内核(implicit kernel)来克服许多函数设计上的限制。
本研究的主要贡献是:
提出神经过程(Neural Processes),这是一种结合了神经网络和随机过程的优点的模型。
我们将神经过程(NP)与元学习(meta-learning)、深层潜变量模型(deep latent variable models)和高斯过程(Gaussian processes)的相关工作进行了比较。鉴于NP与这些领域多有相关,它们让许多相关主题之间可以进行比较。
我们通过将NP应用于一系列任务,包括一维回归、真实的图像补完、贝叶斯优化和contextual bandits来证明了NP的优点和能力。
神经过程模型
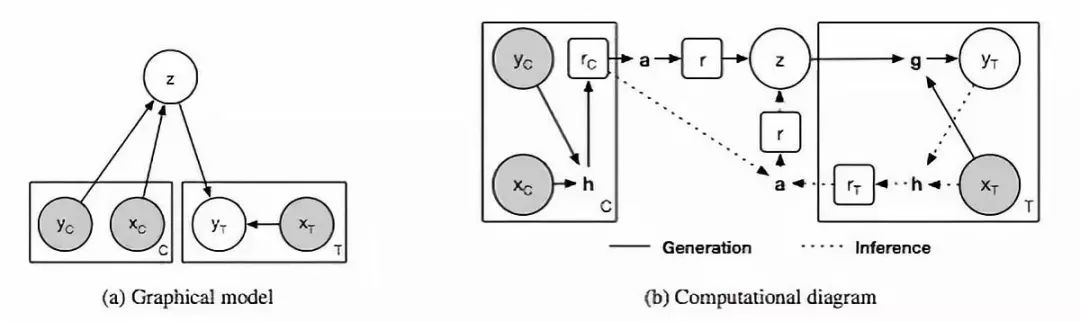
图1:神经过程模型。
(a)neural process的图模型,x和y分别对应于y = f(x)的数据,C和T分别表示上下文点和目标点的个数,z表示全局潜变量。灰色背景表示观察到变量。
(b)neural process的实现示意图。圆圈中的变量对应于(a)中图模型的变量,方框中的变量表示NP的中间表示,粗体字母表示以下计算模块:h – encoder, a – aggregator和g – decoder。在我们的实现中,h和g对应于神经网络,a对应于均值函数。实线表示生成过程,虚线表示推理过程。
在我们的NP实现中,我们提供了两个额外的需求:上下文点的顺序和计算效率的不变性(invariance)。
最终的模型可归结为以下三个核心组件(见图1b):
从输入空间到表示空间的编码器(encoder)h,输入是成对的
上下文值,并为每对生成一个表示
。我们把h参数化为一个神经网络。
聚合器(aggregator)a,汇总编码器的输入。
条件解码器(conditional decoder)g,它将采样的全局潜变量z以及新的目标位置
作为输入,并为对应的
的值输出预测。
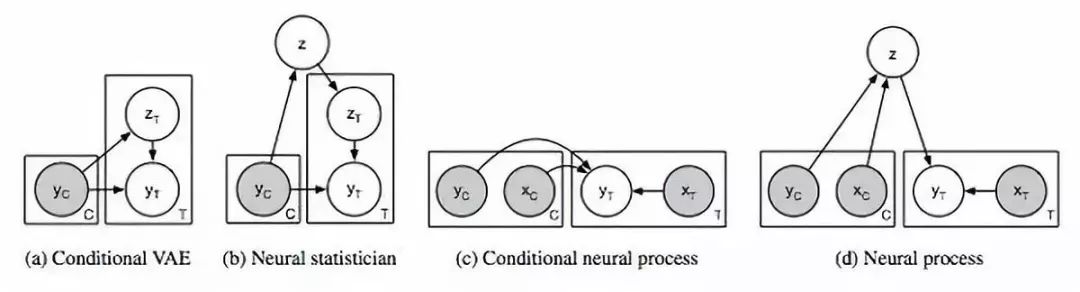
图2:相关模型(a-c)和神经过程(d)的图模型。灰色阴影表示观察到变量。C表示上下文变量,T表示目标变量,即给定C时要预测的变量。
结果
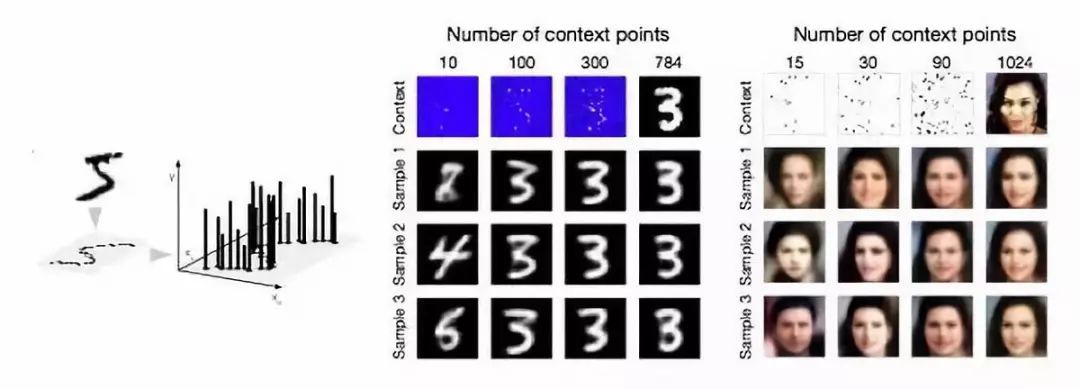
图4. MNIST和CelebA上的像素化回归
左边的图展示了一张图像完成像素化可以框定为一个2-D回归任务,其中f(像素坐标)=像素亮度。右边的图展示了图像实现MNIST和CelebA的结果。顶部的图像对应提供给模型的上下文节点。为了能够更清晰的展现,未被观察到的点在MNIST和CelebA中分别标记为蓝色和白色。在给定文本节点的情况下,每一行对应一个不同的样本。随着文本节点的增加,预测像素越来越接近底层像素,且样本间的方差逐渐减小。
图5. 用神经过程对1-D目标函数进行汤普森抽样
这些图展示了5次迭代优化的过程。每个预测函数(蓝色)是通过对一个潜变量(latent variable)的采样来绘制的,其中该变量的条件是增加文本节点(黑色)的数量。底层的ground truth函数被表示为一条黑色虚线。红色三角形表示下一个评估点(evaluation point),它对应于抽取的NP曲线的最小值。下一个迭代中的红色圆圈对应于这个评估点,它的底层ground truth指将作为NP的一个新文本节点。
表1. 使用汤普森抽样对贝叶斯优化
优化步骤的平均数需要达到高斯过程生成的1-D函数的全局最小值。这些值是通过随机搜索采取步骤数来标准化的。使用恰当的核(kernel)的高斯过程的性能等同于性能的上限。
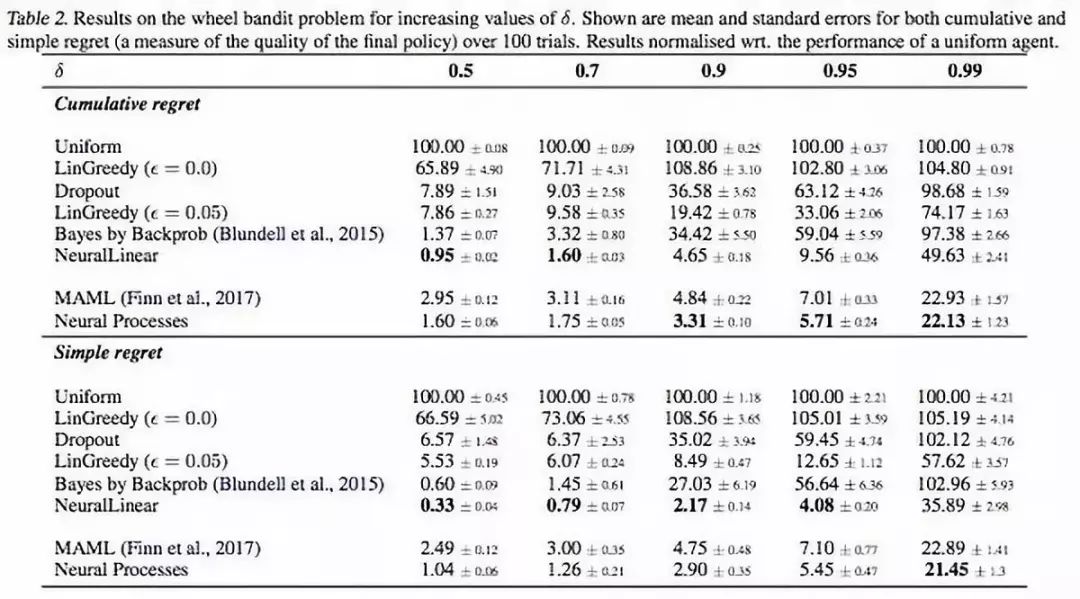
表2. 增加δ值后wheel bandit问题的结果
结果表示的是超过100次的累加regret和简单regret的平均误差和标准误差。结果归一化了一个统一体(uniform agent)的性能。
讨论
我们介绍了一组结合随机过程和神经网络优点的模型,叫做神经过程。NPs学会在函数上表示分布,并且测试时根据一些文本输入做出灵活的预测。NPs不需要亲自编写内核,而是直接从数据中学习隐式度量(implicit measure)。
我们将NPs应用于一些列回归任务,以展示它们的灵活性。本文的目的是介绍NPs,并将它与目前正在进行的研究做对比。因此,我们呈现的任务是虽然种类很多,但是维数相对较低。将NPs扩展到更高的维度,可能会大幅度降低计算复杂度和数据驱动表示(data driven representations)。
识别下图二维码,加“数盟社区”为好友,回复暗号“入群”,加入数盟社区交流群,群内持续有干货分享~~
本周干货内容:新一代人工智能「产业推动的核心理论」
媒体合作请联系:
邮箱:xiangxiaoqing@stormorai.com