学界 | 面向无监督任务：DeepMind提出神经离散表示学习生成模型VQ-VAE

会员服务 ·

学界 | 面向无监督任务：DeepMind提出神经离散表示学习生成模型VQ-VAE

2017 年 11 月 10 日 机器之心

选自arXiv

机器之心编译

参与：路雪、李泽南

DeepMind 最近提出的 VQ-VAE 是一种简单而强大的生成模型，结合向量量化和变分自编码器学习离散表示，实现在图像识别、语音和对话等任务上的无监督学习。

近期，图像、音频、视频领域生成模型的发展产生了惊人的案例与应用。同时，few-shot 学习、域适应或强化学习这样具有挑战性的任务也极为依赖从原始数据学习到的表征。但以无监督方式训练的通用表征的有效性仍无法成为该领域的主流方法。

最大似然和重构误差（reconstruction error）是在像素域中训练无监督模型常用的两种目标函数，但是它们的有效性取决于使用特征的特定应用。DeepMind 的目标是构建一个模型，在其潜在空间（latent space）中保存数据的重要特征，同时优化最大似然。正如 [7] 中的研究，最好的生成模型（以最大似然来衡量）是那些没有隐变量但是具备强大解码器的模型（如 PixelCNN）。在这篇论文中，DeepMind 提出学习离散、有用的隐变量也是一种很好的方法，并在多个领域中进行证实。

使用连续特征学习表示是之前很多研究的重点，但是 DeepMind 把目光放在离散表示上，离散表示有可能更适合 DeepMind 感兴趣的很多模态（modality）。语言是内在离散的，类似地，语音通常表示为符号序列。图像通常可以通过语言进行精确描述 [40]。此外，离散表示适合复杂的推理、规划和预测性学习（如，如果下雨了，我就打伞）。在深度学习中使用离散隐变量证明，已经开发出难度高、强大的自回归模型，可用于对离散变量的分布进行建模 [37]。

这篇论文中，DeepMind 介绍了一族新的生成模型，通过对（离散）隐变量的后验分布进行新型参数化，成功地将变分自编码器（VAE）框架和离散隐变量表示结合起来。该模型依赖于向量量化（vector quantization，VQ），易于训练，不会出现大的变量，避免「后验崩溃」（posterior collapse）问题，该问题通常由被忽略的隐变量引起，对很多具有强大解码器的 VAE 模型来说都是个难题。此外，该模型也是首个离散隐变量 VAE 模型，其性能和连续隐变量 VAE 模型类似，同时还具备离散分布的灵活性。DeepMind 将这种模型命名为 VQ-VAE。

因为 VQ-VAE 可以有效利用潜在空间，它可以有效地对通常跨越数据空间多个维度的重要特征进行建模（例如对象跨越图像中的多个像素、语音对话中的音素、文本片段中的信息等等），而非把注意力集中在噪声或其他细微之处——这些细节往往是局部的。

最后，当 VQ-VAE 发现了一种模态的优秀离散隐变量结构，我们就可以在这些离散随机变量上训练强大的先验，得到有意义的样本和有用的应用。例如，在语音任务中，我们可以在没有任何监督或单词音素先验知识的情况下发现语言的潜在结构。此外，我们可以给解码器赋予说话者的角色，让它展开对话，如让语音在两个说话者之间传递，但不改变说话内容。DeepMind 还在论文中展示了利用此方法在强化学习环境中学习长期结构的高性能。

这篇论文的贡献可概括为：

介绍 VQ-VAE 模型，这是一个简单模型，使用离散隐变量，不会出现「后验崩溃」和变量问题。
证明离散隐变量模型（VQ-VAE）和它在 log 似然中的连续隐变量模型的性能一样好。
当和强大的先验一起出现时，DeepMind 的样本在大量应用（比如语音和视频生成）上都是连贯且高质量的。
证明可以在无监督的情况下，通过原材料学习语言，并展示了无监督说话者对话的应用。

VQ-VAE

或许和 DeepMind 的方法联系最紧密的就是 VAE。VAE 包括以下几个部分：1）一个编码器网络，对后验分布 q(z|x) 进行参数化，z 是离散隐随机变量，x 为输入数据；2）先验分布 p(z)；3）一个解码器，它的输入数据分布是 p(x|z)。

通常，VAE 中的后验分布和先验分布呈对角协方差分布，允许使用高斯重参数化 [32, 23]。其扩展包括自回归先验和后验模型 [14]、常规流（normalising flow）[31, 10]，和逆自回归后验模型 [22]。

这篇论文介绍了 VQ-VAE，该模型使用离散隐变量，受向量量化的启发用一种新的方式进行训练。后验和先验分布是明确分类的，从这些分布中提取的样本可通过嵌入表进行索引。然后将这些嵌入作为解码器网络的输入。

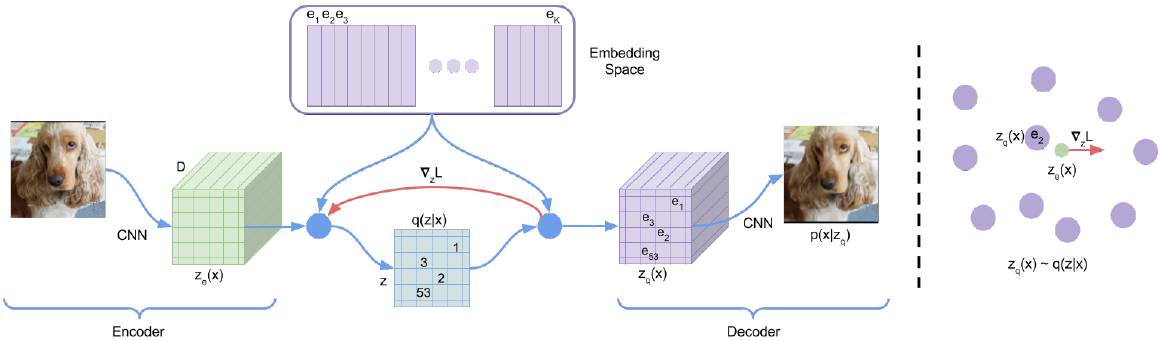
图 1. 左：VQ-VAE 图示。右：嵌入空间可视化。编码器 z(x) 的输出映射到最近点 e_2。梯度∇zL（红色）使编码器改变输出，从而改变下一个前向传输的配置。

图 2. 左：ImageNet 128x128x3 图像，右：潜在空间为 32x32x1、K=512 的 VQ-VAE 输出的重构结果。

图 5. 上方：原始图像，下方：两阶段 VQ-VAE 的重构结果，使用 3 个隐变量对整个图像（27 bits）进行建模，这样的模型仍然不能对图像进行完美重构。重构结果是由第一阶 VQ-VAE 的 21×21 潜在域中的第二个 PixelCNN 先验采样而来，随后被标准 VQ-VAE 解码器解码为 84×84。很多原始场景，包括纹理、房间布局和附近的墙壁都保留原状，但模型没有试图去储存像素值，这意味着纹理是由 PixelCNN 生成的。

论文：Neural Discrete Representation Learning

论文链接：https://arxiv.org/abs/1711.00937

论文第一作者 Aaron van den Oord 也在 GitHub 上展示了新模型的一些结果：https://avdnoord.github.io/homepage/vqvae/

摘要：在无监督情况下学习有意义的表示是机器学习的一个核心挑战。在本论文中，我们提出了一个简单却强大的生成模型，该模型可以学习此类离散表示。我们提出了向量量化-变分自编码器（Vector Quantised-Variational AutoEncoder，VQ-VAE），它与 VAE 在两个关键的方面存在不同：1. 编码器网络输出离散而不是连续的代码；2. 先验是学习的，而非静止的。为了学习离散隐变量表示，我们吸收了向量量化（VQ）的思路。使用 VQ 方法可以让模型绕过「后期崩溃」的问题——隐变量在遇到强大的自回归解码器时被忽略，这种问题通常会在 VAE 框架中出现。通过让这些表示和自回归先验配对，模型可以生成高质量的图像、视频、语音，以及高质量对话，也可以在无监督的情况下学习音素，本研究进一步证明了已学得表示的实用性。