线性代数应该这样讲(四)-奇异值分解与主成分分析

在《线性代数这样讲(二)》(以下简称「二」)中,小夕详细讲解了特征值与特征向量的意义,并且简单描述了一下矩阵的特征值分解的意义和原理。本文便基于对这几个重要概念的理解来进一步讲解SVD分解。
回顾一下,在「二」中,小夕讲过一个方阵W可以分解为它的特征向量矩阵eVec与特征值矩阵eVal相乘的形式,即用 eVec * eVal * eVec-1 来近似原方阵W。

那么问题来啦,如果我们的矩阵不是方阵呢,比如是一个m*n(m≠n)的矩阵呢?可不可以也分解成特征值和特征向量的形式呢?
显然,严格的特征值和特征向量当然不可以啦,由于分解后,存在eVec的逆矩阵eVec-1,因此eVec一定是方阵,而eVec是方阵的话,eVec * eVal * eVec-1的结果也肯定是方阵啦,当然不能近似原矩阵。但是我们可以定义一个意义类似,但是数学上行得通的定义:
对于维度为m*n且m≠n的矩阵W,我们可以将其分解为U*∑*V的形式,其中U的维度为m*m,∑的维度为m*n,V的维度是n*n,这样让U依然代表着“特征向量”的意思,V也代表“特征向量”的意思,∑就代表“特征值”的意思,可以吗?
等等!在《线性代数这样讲(一)》中讲过矩阵乘法,那么在计算U*∑的时候,是拿U中的每一行去乘以特征值矩阵,因此U中的每一列就是一个特征向量(回顾一下,每个特征向量对应一个特征值。还不理解的童鞋用笔和纸体会一下),但是到了(U*∑)的结果去乘V的时候,是拿V的每一列去跟之前的结果相乘,因此显然V的每一行是一个特征向量,所以这里为了避免分解后在使用U和V时发生歧义,我们用U*∑*VT来描述分解的结果,这样U和V就都是一列一个“特征向量”啦。
这里,U里的向量我们定义为左奇异向量,V里的向量我们定义为右奇异向量,它们的意义就暂且理解为跟特征向量差不多。显然,∑就可以理解为跟之前的特征值矩阵意义差不多啦,因此∑的对角线上的值就相当于之前的特征值,这里叫做奇异值,对角线之外的值也跟以前一样,全为0。这个分解过程就叫奇异值分解。
好啦,定义好了,那么如何将一个m*n的矩阵分解成这三个奇异矩阵呢?

前方低能预警!下面这部分可看可不看,纯数学过程我们就不多care啦,不感兴趣的童鞋可以快速往下划~
对于m*n的矩阵W,其转置WT当然就是n*m啦,所以WT*W就是n*n的方阵,然后利用「二」中提到的特征值分解将其分解出若干特征值及其特征向量,因此对于分解出的每个特征值\lambda_i及其对应的特征向量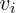
这里的每个特征向量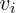
然后我们对每个
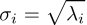
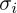
然后我们对于每个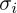
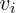
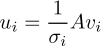
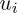
Over。

那么奇异值分解得到的奇异值和左右奇异向量跟特征值与特征向量相比,除了意义相似,有没有什么不同呢?
这里很重要的一点性质就是,将奇异值从大到小排序后,大部分情况下,前几个奇异值(约前10%甚至前1%)的和就占据了全部奇异值之和的99%!
而在「二」中,我们讲过,特征值越接近0,就代表这个特征值对应的特征向量越没有意义(越没有存在感),当特征值为0时,直接表示可以删掉这个特征向量(这个坐标轴),删掉后不会给原矩阵(原映射)带来任何信息量损失。因此,奇异值分解的这个性质在非常多的机器学习场合下可以发挥重要的作用。

比如我们的机器学习任务中,由专家选取或者深度学习的前几层学习到了10000个特征,而这10000个特征完全有可能是高度冗余的,(比如某一维度x1与另一维度x2恒满足x1=2*x2,这时就完全可以删掉其中一个维度,因为一个维度的值完全可以由另一维度计算出来,因此删掉后不会损失任何信息),那么我们想要除掉其中的冗余特征,或者说我们仅仅想用100个特征去描述这10000个特征所描述的东西,怎么办呢?
用奇异值分解就会非常简单。假如我们有9000个样本,那么样本及其对应的特征就组成了一个9000*10000的矩阵X,那么我们用U*∑*VT去逼近X,并且将U限制为9000*100,∑为100*100,VT为100*10000(标准的、一定无信息损耗的奇异值分解是U为9000*9000,∑为9000*10000,VT为10000*10000),这时运用奇异值分解后,就得到了9000*100的左奇异矩阵,显然这就代表着用100维的新特征去重新描述这9000个样本。而右奇异矩阵就代表着如何将100维的新特征映射回10000维的旧特征。显然,奇异值矩阵中的每个奇异值就代表着每个新特征对于描述样本的重要性啦。
这样就成功的完成了降维的操作。
当然啦,实际中,我们往往不知道降到多少维是性价比最高的,因此,我们可以选择保留旧特征描述的99%的信息量。
这时,比如10000维的旧特征,通过前面所述的计算和排序奇异值,算出保留99%的信息量(即前n个奇异值之和除以总奇异值之和大于99%)时需要保留前多少个奇异值,比如算出来的值是前87个大奇异值,那么我们就可以将原来10000维的旧特征空间用仅有87维的新特征空间描述啦~而仅仅会丢失1%的信息量哦。
诶?我好想不小心把PCA给讲完了。。。没错,通过上面的方式将SVD应用于维度的压缩的方法,就是每个学机器学习的人一定听说过的主成分分析(PCA)。
(走过路过不要错过~买SVD送PCA啦~还送美美的老板娘哦)