「工业落地」图神经网络+推荐系统

2020 年 4 月 24 日 机器学习与推荐算法

作者：一块小蛋糕

原文链接：https://zhuanlan.zhihu.com/p/133739758

最近在复现PinSage，今天也想聊一聊这个第一次将GCN应用于工业级推荐系统的图算法，论文来自《Graph Convolutional Neural Networks for Web-Scale Recommender Systems》。这个系统是斯坦福和Pinterest公司合作的成果，其理论基础是斯坦福前一年的一篇GCN论文《Inductive Representation Learning on Large Graphs》。

本文将按照PinSage的理论背景-GraphSAGE，PinSage的思想以及PinSage的工程技巧三个方面理解PinSage，最后摘取部分PinSage代码加深理解。

1、PinSage的理论背景-GraphSAGE

PinSage是在GraphSAGE的基础上发展而来，想要明白PinSage背后的原理就要先了解GraphSAGE。

1.1 GraphSAGE初衷

GraphSAGE提出的初衷是改变图学习中的惯有模式：直推式(transductive)学习，即在固定的图上直接学习每个节点的Embedding，每次学习只考虑当前数据。之前的图上的学习算法基本都是这一模式，如DeepWalk，LINE，GCN等都是如此。

这种模式的局限性非常明显，工业界的大多数业务场景中，图中的结构和节点都不可能是固定的，是会变化的，比如，用户集合会不断出现新用户，用户的关注关系集合也是不断增长的，内容平台上的文章更是每天都会大量新增。在这样的场景中，直推式学习需要不停地重新训练，为新的节点学习Embedding，这给图学习在工业界落地带来了极大的困难。

GraphSAGE提出了图上学习的新模式：归纳(inductive)学习，即学习在图上生成节点Embedding的方法而不是直接学习节点的Embedding。GraphSAGE正是以学习聚合节点邻居生成节点Embedding的函数的方式，将GCN扩展成归纳学习任务。

归纳学习的优势在于可以从特殊泛化到一般，对未知节点上的未知数据也有区分性。这个优势使得它能完美应对工业界的各种图动态变化的场景。

除了学习模式外，GraphSage相比GCN还有效率上的大幅提升，原有的GCN训练算法是针对全图的拉普拉斯矩阵计算，其计算复杂度之高也是GCN在工业界落地的一大阻碍，而GraphSage同样解决了这一问题。

1.2 GraphSAGE算法框架

GraphSAGE框架的核心是学习如何聚合节点的邻居特征生成当前节点的信息，学习到这样一个聚合函数之后，不管图结构和图信息如何变化，都可以通过当前已知各个节点的特征和邻居关系，生成节点的embedding。

GraphSage框架中包含两个很重要的操作：Sample采样和Aggregate聚合。这也是其名字GraphSage(Graph SAmple and aggreGatE)的由来。

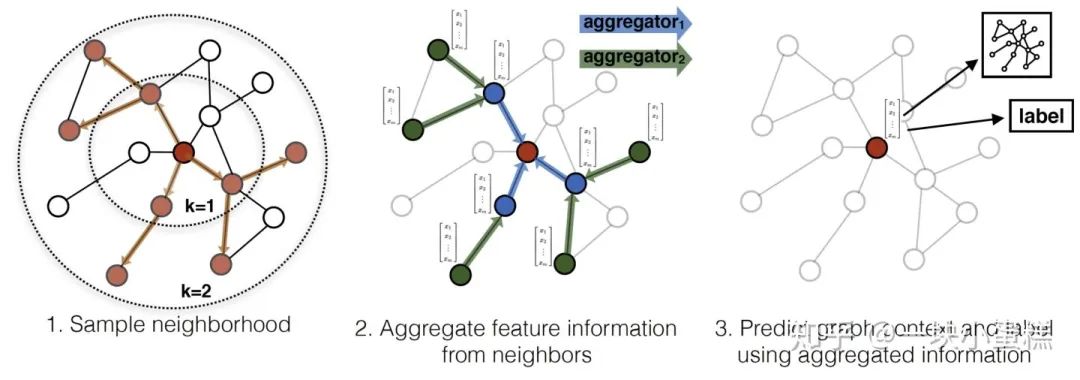
GraphSage的核心算法，embedding生成算法，也是由这两部分组成：Sample和Aggregate。

GraphSage的minibatch算法的思路是先采样计算所需的全部节点信息，即Sample阶段，对应上述伪代码的2-7行，表示某种随机采样方法，这里采样操作的目的是降低迭代计算复杂度，如果不采样使用全部邻居节点的话，每次迭代生成节点信息的时间无法预估，最坏情况会达到全图节点，与原有的GCN算法无异。包含了计算中节点表示所需的全部节点。

这里需要注意一点的是，采样从第K层到第1层，对应的是初始节点集合，即最内层的待学习embedding的节点集合，所以采样过程是从内向外逐层采样每个节点的邻居节点，最内层对应第K层，这一点与上面论文中的Sample图示中是不一致的，容易产生困惑。且每层节点都是在上一层的节点集合基础上扩展而来，即包含前一层的全部节点（伪代码的第3行），与前一层每个节点在当前层的邻居节点（伪代码的第5行）。

这里以K层为例，说明一下采样顺序与集合内的点：

=输入目标节点集合；

=目标节点+其一阶邻居节点；

=目标节点+其一阶邻居节点+其二阶邻居节点；

......；

=目标节点+其一阶邻居节点+二阶邻居节点+...+K阶邻居节点。

其次是算法的聚合阶段，对应上述伪代码的9-15行，这一部分和GraphSage的批量推断过程是一致的。聚合操作是从第1层到第K层聚合，初始的第0层节点embedding 来自于采样结果集合中节点的输入特征信息，集合即对应最外层的采样节点集合，由此开始，从外向内逐层聚合K次直到最中心的输入节点，每一次聚合，都是把当前层中的节点在上一层中的邻居节点的embedding 挑出来聚合得到邻居聚合特征，再与当前层中节点当前的embedding 拼接，并通过全连接层转换，得到该节点的新的embedding 。

可以认为是每一次聚合都是完成一次：将k阶邻居的信息聚合到k-1阶邻居上，k-1阶邻居的信息聚合到k-2阶邻居上，....，1阶邻居的信息聚合到输入节点上的过程。

1.3 GraphSage的参数学习

GraphSage中需要学习的参数是上面K个层中每层的聚合函数和全连接层对应的参数，定义好损失函数后，都可以通过随机梯度下降学习。

GraphSage的损失函数分为两种情况：无监督场景下，节点特征作为一种静态信息提供给下游应用，此时的损失函数应该让结构上邻近的节点拥有相似的表示，而不相近的节点表示大不相同，论文中给出的损失函数如下：

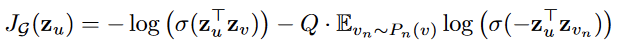
而对于有监督场景，损失函数则视具体业务而定，比如分类问题可以使用cross-entropy，也可以在无监督损失的基础上做修改，这里是一个比较灵活的尝试点。

1.4 GraphSage的聚合函数

GraphSage中作者给出了三种聚合函数：

Mean 聚合：当前节点的邻居节点的embedding求平均作为当前节点的embedding
Convolutional 聚合：GCN aggregator变种，取当前节点及其邻居节点的embedding的平均，经过一层全连接后得到当前节点的embedding

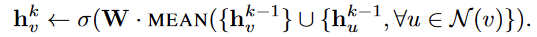
这个聚合函数和GraphSage中使用的聚合函数的差别在于没有拼接操作，GraphSage聚合中的拼接操作可以视为是不同层之间的直连操作，对于提升性能大有好处。论文中关于这一段的讲解中有一句感觉有些歧义，有待验证。

LSTM聚合：LSTM聚合的优势是表达能力强，跟其他聚合函数最大的不同是不具有对称性，即对节点集合的顺序敏感。这里作者只是随机取了所有邻居节点的其中一种随机序列聚合。
Pooling聚合：把各个邻居节点的embedding单独经过一个MLP，在所有的结果embedding中做element-wise的max-pooling或是mean-pooling，如下图：

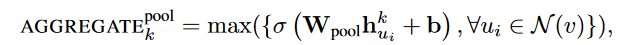
实验结果证明：LSTM聚合和Pooling聚合都是远好于其他聚合方法的，但LSTM的耗时尤其高，因此最优选择也就是Pooling聚合。

同时，作者也给出GraphSage的实践中，K=2，S1*S2<=500就可以达到很高的性能，这说明一般只需要扩展到节点的2阶邻居，每次扩展约20~30个邻居即可。

2、PinSage理解

2.1 PinSage算法思想

有了GraphSage的理解之后，PinSage的原理就比较好懂了。

PinSage的算法和GraphSage很相似，略有不同，论文中分为Convolve算法和minibatch两个讲解。其中minibatch的流程和上述GraphSage中minibatch算法的流程一致，

Convolve算法相当于GraphSage算法的聚合阶段过程，是PinSage中的单层图卷积算法，实际执行中，对K层邻居的每一层都执行一遍图卷积以得到不同阶邻居的信息。主要操作包括：

- 1）聚合邻居：所有的邻居节点都经过一层dense层，再由聚合器或池化函数（如元素平均，加权和等）将所有邻居节点的信息聚合成一个vector （伪码第一行）

- 2）更新当前节点的embedding：将目标节点的当前embedding与聚合后的邻居向量拼接后再经过一层dense层（伪码第二行）

- 3）归一化：对目标节点embedding归一化（伪码第三行）

Convolve算法和GraphSage的聚合阶段的不同之处在于邻居节点的embedding聚合前经过了一层dense层。

PinSage中的minibatch算法流程和GraphSage也是一致的，但PinSage增加了一些改进：

首先，与GraphSage一样的是，伪码2~7行是邻居采样阶段，PinSage这里创新的一点是将GraphSage的随机采样改为重要性采样，从目标节点开始random-walk，计算各邻居节点的访问数作为邻居节点的重要性权重，最终选取top-t的邻居，这里每个节点的权重在后面聚合阶段也有用到。这个做法的好处一个是邻居节点个数可控，内存占用及计算耗时可预估，这一点其实GraphSage中的随机采样也能做到；另一个好处是聚合邻居节点的过程中可以根据邻居节点的重要性聚合，这一点是GraphSage所没有的。至于K层的采样顺序与每层的节点集合与GraphSage中都是一致的。

然后，仍然与GraphSage一样，伪码9~14行是邻居聚合阶段，只是这里都包含在局部图卷积Convolve操作里了。除了聚合邻居前经过一层dense层，其他过程如K层卷积的顺序，卷积操作节点范围等也都与GraphSage一致。可以参考上一节的讲解。

最后，伪码15~16行是与GraphSage不同的，目标节点与各自邻居聚合之后的embedding并不是直接替换目前节点的当前embedding，而是经过一层dense层后再替换。

2.2 PinSage训练

PinSage中采用的是有监督训练，训练集中标注了相似节点对，其中正样本标签的定义是如果用户在点击item q之后立刻点击了item i，就认为i是q的理想推荐候选。

训练损失使用的是max-margin ranking loss，即最大化正例之间的相似性，同时保证与负例之间相似性小于正例间的相似性。如下：为q对应的负例分布，，是超参。

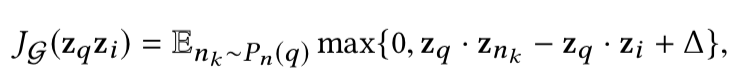
2.3 PinSage的工程技巧总结

上一节中讲述了PinSage算法的全部思想，和GraphSage大致一样，略有不同。而PinSage作为第一个基于GCN的工业级别推荐系统，支撑了数十亿节点和数百亿边，仅仅靠上面的算法思想是不够的，PinSage论文中还介绍了落地过程中采用的大量工程技巧。

负样本生成：首先是简单采样：在每个minibatch包含节点的范围之外随机采样500个item作为minibatch所有正样本共享的负样本集合。但考虑到实际场景中模型需要从20亿的物品item集合中识别出最相似的1000个，即要从2百万中识别出最相似的那一个，只是简单采样会导致模型分辨的粒度过粗，分辨率只到500分之一，因此增加一种“hard”负样本，即对于每个对，和物品q有些相似但和物品i不相关的物品集合。

这种样本的生成方式是将图中节点根据相对节点q的个性化PageRank分值排序，随机选取排序位置在2000~5000的物品作为“hard”负样本，以此提高模型分辨正负样本的难度。

渐进式训练(Curriculum training)：如果训练全程都使用hard负样本，会导致模型收敛速度减半，训练时长加倍，因此PinSage采用了一种Curriculum训练的方式，这里我理解是一种渐进式训练方法，即第一轮训练只使用简单负样本，帮助模型参数快速收敛到一个loss比较低的范围；后续训练中逐步加入hard负样本，让模型学会将很相似的物品与些微相似的区分开，方式是第n轮训练时给每个物品的负样本集合中增加n-1个hard负样本。
样本的特征信息：Pinterest的业务场景中每个pin通常有一张图片和一系列的文字标注（标题，描述等），因此原始图中每个节点的特征表示由图片Embedding（4096维），文字标注Embedding（256维），以及节点在图中的度的log值拼接而成。其中图片Embedding由6层全连接的VGG-16生成，文字标注Embedding由Word2Vec训练得到。
基于random walk的重要性采样：用于邻居节点采样，这一技巧在上面的算法理解部分已经讲解过，此处不再赘述。
基于重要性的池化操作：这一技巧用于上一节Convolve算法中的函数中，聚合经过一层dense层之后的邻居节点Embedding时，基于random walk计算出的节点权重做聚合操作。据论文描述，这一技巧在离线评估指标中提升了46%。
on-the-fly convolutions：快速卷积操作，这个技巧主要是相对原始GCN中的卷积操作：特征矩阵与全图拉普拉斯矩阵的幂相乘。涉及到全图的都是计算量超高，这里GraphSage和PinSage都是一致地使用采样邻居节点动态构建局部计算图的方法提升训练效率，只是二者采样的方式不同。
生产者消费者模式构建minibatch：这个点主要是为了提高模型训练时GPU的利用率。保存原始图结构的邻居表和数十亿节点的特征矩阵只能放在CPU内存中，GPU执行convolve卷积操作时每次从CPU取数据是很耗时的。为了解决这个问题，PinSage使用re-index技术创建当前minibatch内节点及其邻居组成的子图，同时从数十亿节点的特征矩阵中提取出该子图节点对应的特征矩阵，注意提取后的特征矩阵中的节点索引要与前面子图中的索引保持一致。这个子图的邻接列表和特征矩阵作为一个minibatch送入GPU训练，这样一来，convolve操作过程中就没有GPU与CPU的通信需求了。训练过程中CPU使用OpenMP并设计了一个producer-consumer模式，CPU负责提取特征，re-index，负采样等计算，GPU只负责模型计算。这个技巧降低了一半的训练耗时。
多GPU训练超大batch：前向传播过程中，各个GPU等分minibatch，共享一套参数，反向传播时，将每个GPU中的参数梯度都聚合到一起，执行同步SGD。为了适应海量训练数据的需要，增大batchsize从512到4096。为了在超大batchsize下快速收敛保证泛化精度，采用warmup过程：在第一个epoch中将学习率线性提升到最高，后面的epoch中再逐步指数下降。
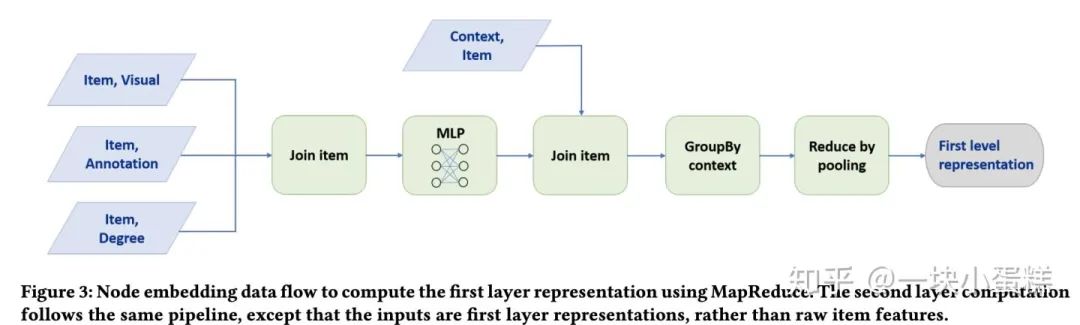
使用MapReduce高效推断：模型训练完成后生成图中各个节点的Embedding过程中，如果直接使用上述PinSage的minibatch算法生成Embedding，会有大量的重复计算，如计算当前target节点的时候，其相当一部分邻居节点已经计算过Embedding了，而当这些邻居节点作为target节点的时候，当前target节点极有可能需要再重新计算一遍，这一部分的重复计算既耗时又浪费。

因此针对pin-to-board的二部图构建了两个MapReduce任务：1）执行聚合操作计算所有pins的Embedding 2）将pins和对应的boards匹配，基于采样后的board邻居特征（即pins的Embedding）做pooling得到board的Embedding

两个任务执行完后第一层的卷积操作就算执行完了，如果有K层卷积操作，类似地再重复执行K-1遍这两个MapReduce任务，得到全量节点的Embedding后，导入到数据库中供下游应用查询。

Embedding近邻查询：为了在线查询item的Embedding需要，有两种高效查询的方法：近似KNN：《Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions》，和基于 Weak AND 操作的两级检索：《Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions》

3、PinSage源码学习

因业务代码不方便放出，只拿了最初上手学习的demo代码用于讲解。代码是基于tf2.0的，只是实现了PinSage的简单采样和卷积过程，并未加入其它工程技巧.

首先是Convolve操作, 分别表示聚合前每个邻居节点需经过的dense层以及邻居节点聚合后的Embedding与目标节点Embedding拼接后需经过的dense层。代码的总体流程和上述PinSage的伪码流程一致。

import numpy as np
import networkx as nx
import tensorflow as tf
class Convolve(tf.keras.Model):
    def __init__(self, hidden_channels):
        super(Convolve, self).__init__()
        self.Q = tf.keras.layers.Dense(units=hidden_channels, activation=tf.keras.layers.LeakyReLU())
        self.W = tf.keras.layers.Dense(units=hidden_channels, activation=tf.keras.layers.LeakyReLU())
    def call(self, inputs):
        # embedding.shape = (batch, node number, in_channels)
        embeddings = inputs[0]   # 所有节点的Embedding
        # weight.shape = (node number, node number)
        weights = inputs[1]   # 所有边权重
        # neighbor_set.shape = (node number, neighbor number)  ==> (节点数，邻居数)
        neighbor_set = inputs[2]  # 针对每个节点采样的邻居节点id集合
        # neighbor_embeddings.shape = (batch, node number, neighbor number, in channels)
        # 所有邻居节点对应的Embedding
        neighbor_embeddings = tf.keras.layers.Lambda(lambda x, neighbor_set: tf.transpose(tf.gather_nd(tf.transpose(x, (1, 0, 2)),
                                                                                                       tf.expand_dims(neighbor_set, axis=-1)
                                                                                                       ),
                                                                                          (2, 0, 1, 3)
                                                                                          ),
                                                     arguments={'neighbor_set': neighbor_set})(embeddings)
        # neighbor_hiddens.shape = (batch, node number, neighbor number, hidden channels)
        neighbor_hiddens = self.Q(neighbor_embeddings)  # 所有的邻居Embedding经过第一层dense层

        # indices.shape = (node number, neighbor number, 2)
        node_nums = tf.keras.layers.Lambda(lambda x: tf.tile(tf.expand_dims(tf.range(tf.shape(x)[0]), axis=1),
                                                             (1, tf.shape(x)[1])))(neighbor_set)
        indices = tf.keras.layers.Lambda(lambda x: tf.stack(x, axis=-1))([node_nums, neighbor_set])  # 所有邻居节点及其对应的目标节点id

        # neighbor weights.shape = (node number, neighbor number)
        neighbor_weights = tf.keras.layers.Lambda(lambda x, indices: tf.gather_nd(x, indices),
                                                  arguments={"indices": indices})(weights)    # 提取所有要计算的邻居边的权重
        # neighbor weights.shape = (1, node number, neighbor number, 1)
        neighbor_weights = tf.keras.layers.Lambda(lambda x: tf.expand_dims(tf.expand_dims(x, 0), -1))(neighbor_weights)

        # weighted_sum_hidden.shape = (batch, node number, hidden channels)  # 对所有节点的邻居节点Embedding，根据其与目标节点的边的权重计算加权和
        weighted_sum_hidden = tf.keras.layers.Lambda(lambda x: tf.math.reduce_sum(x[0] * x[1], axis=2) / (tf.reduce_sum(x[1], axis=2)+1e-6))([neighbor_hiddens, neighbor_weights])

        # concated_hidden.shape = (batch, node number, in channels + hidden channels)  # 节点的原始Embedding与每个节点的邻居加权和Embedding拼接
        concated_hidden = tf.keras.layers.Concatenate(axis=-1)([embeddings, weighted_sum_hidden])

        # hidden_new shape = (batch, node number, hidden_channels)
        hidden_new = self.W(concated_hidden)   # 拼接后的Embedding经过第二层dense层

        # normalized.shape = (batch, node number, hidden_channels)  # 结果Embedding规范化
        normalized = tf.keras.layers.Lambda(lambda x: x / (tf.norm(x, axis=2, keep_dims=True) + 1e-6))(hidden_new)
        return normalized

然后是minibatch算法，graph使用networkx中的graph表示，

class PinSage(tf.keras.Model):
    def __init__(self, hidden_channels, graph=None, edge_weights=None):
        # hidden_channels用于保存每次卷积convolve操作的输出
        assert type(hidden_channels) is list
        if graph is not None: assert type(graph) is nx.classes.graph.Graph  # 原始图
        if edge_weights is not None : assert type(edge_weights) is list   # 边权重
        super(PinSage, self).__init__()
        # 创建卷积层
        self.convs = list()
        for i in range(len(hidden_channels)):
            self.convs.append(Convolve(hidden_channels=[i]))
        # 在原始图上计算PageRank权重
        self.edge_weights = self.pagerank(graph) if graph is not None else edge_weights
    def call(self, inputs):
        # embeddings.shape = (batch, node number, in channels)
        embeddings = inputs[0]   # 所有节点的Embedding
        # 邻居采样个数
        sample_neighbor_num = inputs[1]
        # 根据边的权重对邻居采样
        # neighbor_set.shape = (node num, neighbor num) ==> (节点数，邻居数)
        neighbor_set = tf.random.categorical(self.edge_weights, sample_neighbor_num)  #针对每个节点采样的邻居集合
        for conv in self.convs:   #经过K层卷积
            embeddings = conv([embeddings, self.edge_weights, neighbor_set])
        return embeddings
    def pagerank(self, graph, damp_rate=0.2):
        # node id must from 0 to any nature number
        node_ids = sorted([id for id in graph.nodes])
        assert node_ids == list(range(len(node_ids)))
        # adjacent matrix
        weights = np.zeros((len(graph.nodes), len(graph.nodes), ), dtype=np.float32)
        for f in graph.nodes:
            for t in list(graph.adj[f]):
                weights[f, t] = 1
        weights = tf.constant(weights)
        # normalize adjacent matrix line by line
        line_sum = tf.math.reduce_sum(weights, axis=1, keep_dims=True)+1e-6
        normalized = weights / line_sum
        # dampping vector
        dampping = tf.ones((len(graph.nodes), ), dtype=tf.float32)
        dampping = dampping / tf.constant(len(graph.nodes), dtype=tf.float32)
        dampping = tf.expand_dims(dampping, 0) # line vector
        # learning pagerank
        v = dampping
        while True:
            v_updated = (1-damp_rate) * tf.linalg.matmul(v, normalized) + damp_rate * dampping
            d = tf.norm(v_updated - v)
            if tf.equal(tf.less(d, 1e-4), True): break
            v = v_updated
        # edge weight is pagerank
        weights = weights * tf.tile(v, (tf.shape(weights)[0], 1))
        line_sum = tf.reduce_sum(weights, axis=1, keepdims=True) + 1e-6
        normalized = weights / line_sum
        return normalized