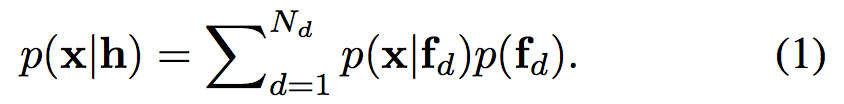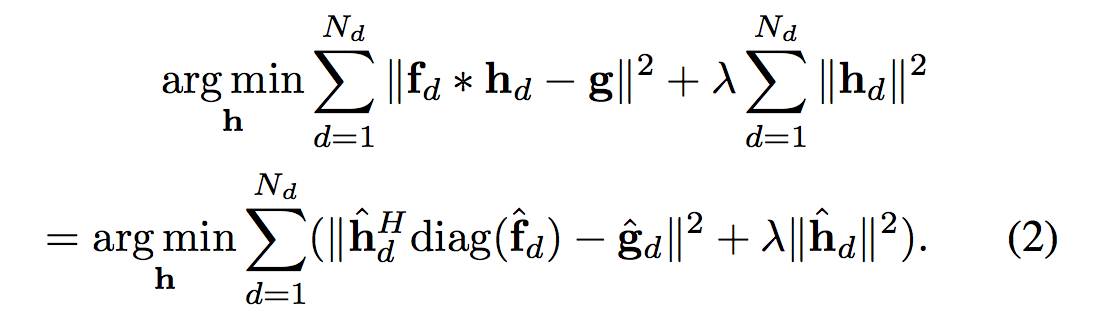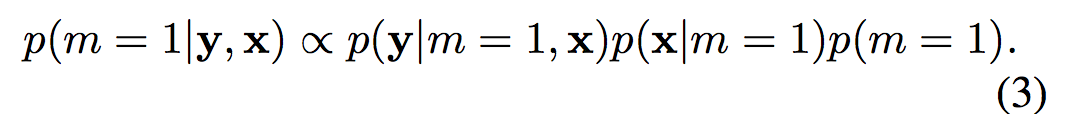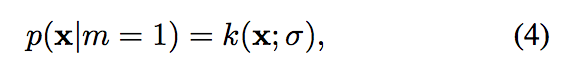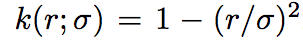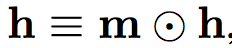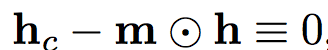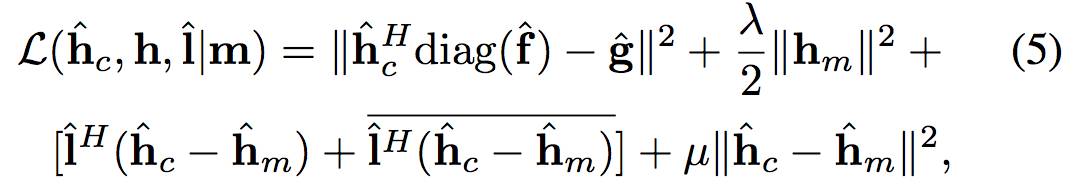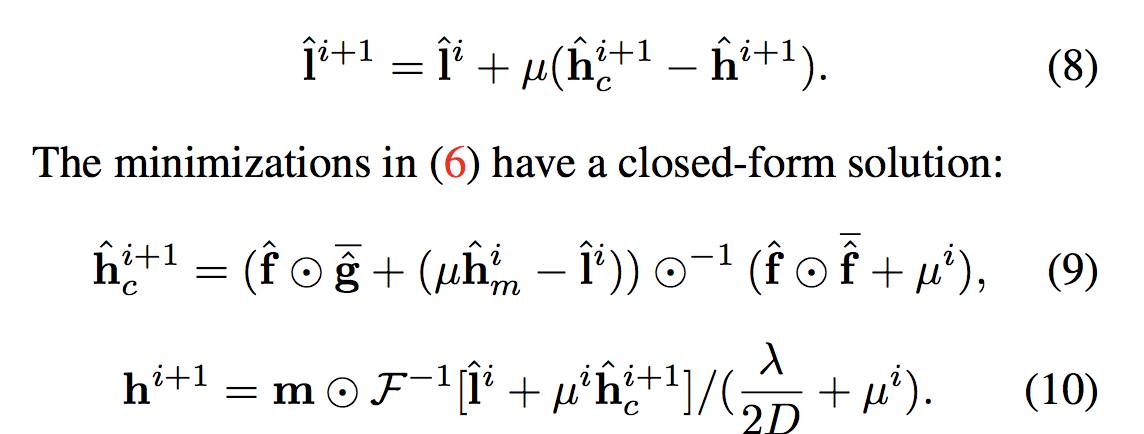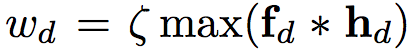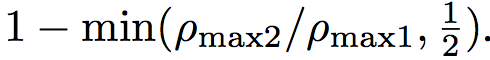论文笔记：通道空间可靠性相关滤波跟踪器

Discriminative Correlation Filter with Channel and Spatial Reliability

发表在CVPR2017 

原文连接：

https://arxiv.org/pdf/1611.08461v1.pdf

大家都知道，基于判别式相关滤波（DCF）跟踪算法的跟踪器在标准数据集上显示出了最先进的性能。标准的DCF表达式使用循环相关，一种可以利用快速傅里叶变换实现快速学习的方法。但是，快速傅里叶变换要求滤波器和被检测的块大小相等，限制了检测的范围。由于滤波是由原样本通过循环位移得到的样本学习得到的，这些样本中包含了一些不真实的样本等，这些窗口问题已经被一些先进的算法所缓解。

DCF方法的另一个缺陷是基于一个假设，目标的形状可以很好的被一个与坐标轴对齐的矩形近似。对于那些形状不规则的目标或者是中空的目标而言，这种假设会使得滤波器学习到一些背景知识，导致跟踪漂移或者跟踪失败。当目标遭遇到遮挡时也会出现这样的问题。

本文作者提出了通道可靠性和空间可靠性的概念，并提出具有通道可靠性和空间可靠性的判别式相关滤波跟踪算法。

空间可靠性调整滤波支持目标中那些更适合跟踪的部分，这不仅可以增大搜索的区域而且可以改善非矩形目标的跟踪性能；

通道可靠性反应了每个通道学习得到的滤波的质量，并在定位中作为特征权重系数。

假设fd（d=1:Nd，总共有Nd个通道）为通道特征，p(fd)为先验知识反应了通道的可靠性，hd（d=1:Nd，总共有Nd个通道）为滤波器，目标的位置x通过最大化以下概率得到：

其中p(x|fd)=[fd*hd](x)。

大多数滤波器都假设特征通道是独立的，所以滤波器通过最小化逐通道相关输出和渴望输出的差异平方之和获得：

（通过Parsevaal’s theorem得到）

aˆ = vec(F[a])是a的傅里叶变换拉成列向量的形式。

diag(a)将向量a转化成对角矩阵的形式。

(·)H是Hermitian转置。

通过令每个通道的梯度等于0，公式（2）可以得到一个闭合解。虽然这种解法很简便，但是这个解会受到边界效应的影响（因为样本是循环移位得到的，且假设每个像素对于滤波器的学习都是等价的）。作者通过改变每个像素对学习滤波器的影响力来解决边界效应的问题，因此提出了一个有效的空间可靠性图谱（spatial reliability map）构建相关滤波器来解决这个问题，并提出一种新的空间约束相关滤波学习框架。

构建空间可靠性图谱

空间可靠性图谱m是一个二值化的图谱，其大小跟图像块的大小相等，表明了每个像素的学习可靠性。在出现表观y的条件下像素x的可能性定义为:

p(y|m=1,x)通过物体的前景/背景颜色模型的贝叶斯法则计算得到。

P(m=1)由前景/背景直方图提取的区域大小之间的比率定义。

其中

有约束的相关滤波学习

为了符号清晰度，在接下来的求导中假设只有一个通道，即Nd=1。

空间可靠性图谱m识别在滤波器学习中应该被忽略的像素，即引入一个限制

这使得公式（2）不能得到一个封闭解。作者引入一个封闭变量

得到如下的增广拉格朗日表达式：

作者使用了ADMM算法来解决这个问题【1】。详细的推导请见作者提供的补充材料。

最终解得

通道可靠性估计

通道可靠性为学习通道可靠性测量和检测可靠性测量的乘积。

通道可靠性测量

检测可靠性测量w=

总体算法流程：

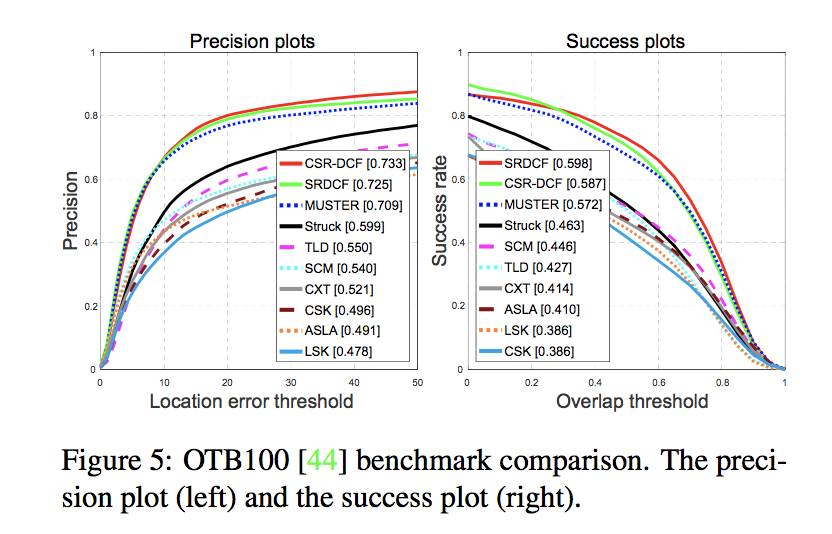
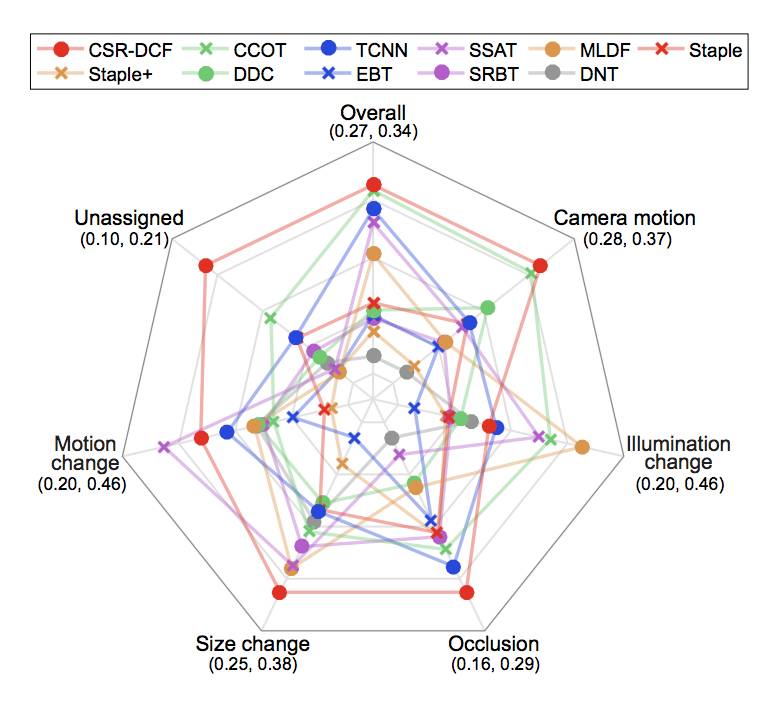
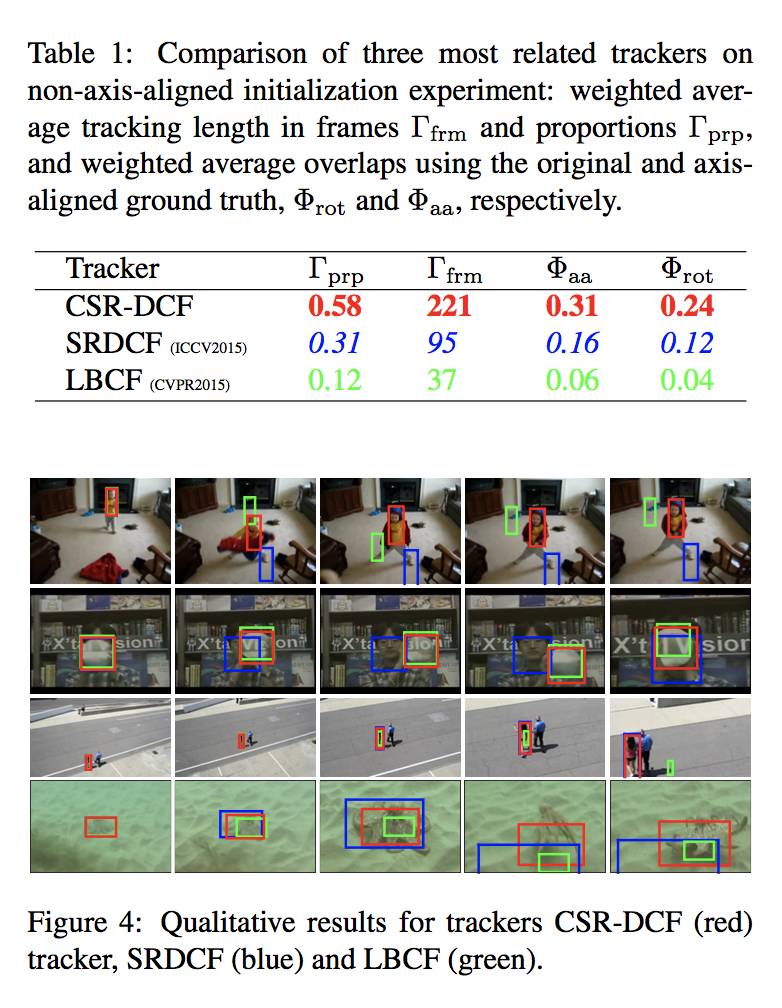
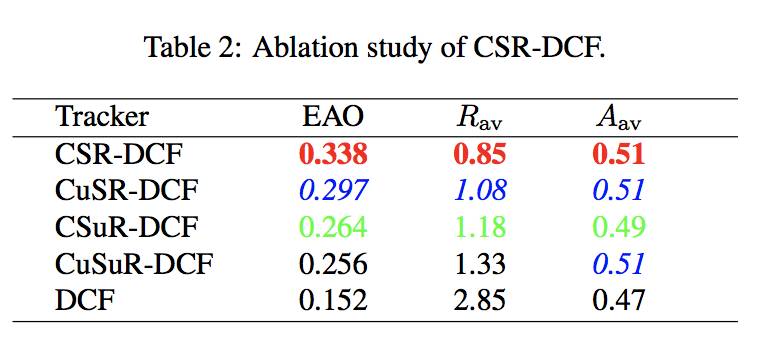
实验部分

【1】S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternat-ing direction method of multipliers. Foundations and Trendsin Machine Learning, 3(1):1–122, 2011. 3

https://arxiv.org/pdf/1611.08461v1.pdf